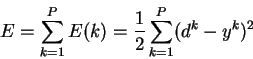2. Метод Розенблатта

Данный метод был предложен Ф.Розенблаттом в 1959 г. для НС, названной персептрон (perceptron). Персептрон рассматривался его автором не как конкретное техническое вычислительное устройство, а как модель работы мозга. Нужно заметить, что после нескольких десятилетий исследований современные работы по искусственным нейронным сетям редко преследуют такую цель. Персептрон имеет пороговую функцию активации, его схема представлена на рис.4.

Рисунок 4 – Однослойный персептрон

Процедуру обучения Розенблатта для однослойного персептрона можно представить так:

где

• x_i — i-тый вход НС;

• d_j — желаемый (идеальный) j-тый выход НС;

• α — коэффициент (скорость обучения) 0<α≤1

Простейший классический персептрон содержит нейрободобные элементы трех типов, назначение которых в целом соответствует нейронам рефлекторной нейронной сети, рассмотренной в предыдущей лекции. S-элементы формируют сетчатку сенсорных клеток, принимающих двоичные сигналы от внешнего мира.

Розенблатт называл такую нейронную сеть трехслойной, однако по современной терминологии, используемой в этой книге, представленная сеть обычно называется однослойной, так как имеет только один слой нейропроцессорных элементов. Однослойный персептрон характеризуется матрицей синаптических связей W от S- к A-элементам. Элемент матрицы отвечает связи, ведущей от i-го S-элемента к j-му A-элементу.

Были выявлены принципиальные неустранимые ограничения однослойных персептронов, и в последствии стал в основном рассматриваться многослойный вариант персептрона, в котором имеются несколько слоев процессорных элементов.

С сегодняшних позиций однослойный персептрон представляет скорее исторический интерес, однако на его примере могут быть изучены основные понятия и простые алгоритмы обучения нейронных сетей.

Весовые коэффициенты меняются только в том случае, если реальное выходное значение не совпадает идеальным выходным значением.

Полный алгоритм обучения Розенблатта строится следующим образом:

1. Весовые коэффициенты НС инициализируются малыми случайными значениями.

2. Подать на вход НС очередной учебный пример.

3. Если выход НС y_j не совпадает с идеальным выходом d_j, то происходит модификация весов по (1).

4. Цикл повторяется с п.2 пока весовые коэффициенты перестанут меняться.

2. Метод Уидроу-Хоффа

Персептрон Розенблатта ограничивается бинарными выходами. Уидроу и Хофф изменили модель Розенблатта. Их первая модель - ADALINE (Adaptive Linear Element) имела один выходной нейрон и непрерывную линейную функцию активации нейронов.

 

(2)

Метод обучения Уидроу-Хоффа известен еще как дельта-правило (delta-rule). Этот метод ставит своей целью минимизацию функции ошибки в пространстве весовых коэффициентов.

 

(3)

где

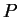• - количество обработанных НС примеров

• E(k) - ошибка для 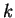-го примера

• y^k - реальный выход НС для -го примера

• d^k - желаемый (идеальный) выход НС для 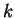-го примера .

Минимизация осуществляется методом градиентного спуска

где

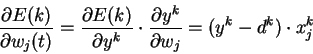
Таким образом, весовые коэффициенты изменяются по правилу

(4)

Полный алгоритм обучения методом Видроу-Хоффа строится следующим образом:

1. Задать скорость обучения a;(0<a<1) задать минимальную ошибку сети 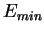; весовые коэффициенты НС инициализируются малыми случайными значениями.

2. Подать на вход НС очередной учебный пример; рассчитать выход НС

3. Скорректировать веса по (4)

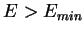
4. Цикл с п.2 повторяется, пока

(где - суммарная среднеквадратичная ошибка НС)