
Ответы Корначук СК71
.pdf
1.10 Кинетика ЯР при периодическом изменении реактивности. Линеаризация уравнений методом малых отклонений.
Кинетика ЯР при периодическом изменении реактивности соответствует работе реактора на постоянном уровне мощности. МЕТОД МАЛЫХ ОТКЛОНЕНИЙ – метод линеаризации нелинейных дифференциальных уравнений, заключающийся в следующем:
–все переменные в уравнении записывают в виде суммы стационарного значения и его малой вариации,
–пренебрегают произведением двух и более вариаций ввиду их малости,
–исключают члены уравнения, описывающие преобразование стационарного состояния,
–оставшиеся члены уравнения являются линейными относительно вариаций переменных и могут быть легко приведены к операторному виду.
|
dN |
|
K N |
6 |
|
|
|
|
dC |
i |
|
|
i |
N iCi ; |
|
||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
iCi ; |
|
|
|
|
|
||||||||||
|
|
|
|
dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
dt |
|
leff |
i |
|
|
(1) |
|
|
|
leff |
(2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выразим из уравнения (2) i Ci и подставим в (1): |
|
|
|
|
|
||||||||||||
|
|
|
|
dN |
|
K |
6 dCi |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
leff |
|
dt |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
i |
|
|
|
(3) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Представим N в виде суммы двух слагаемых: N0 – стационарной величины и δN – малого отклонения. Таким же образом представим Ci в виде суммы Ci0 и δCi.В уравнение (3)
подставим новые переменные N N0 N; Ci Ci0 Ci ;
|
dN |
|
|
d |
|
|
|
|
K |
|
|
|
|
|
K |
6 |
|
d |
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
N |
0 |
|
|
N |
|
|
|
C ; |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dt |
|
|
dt |
|
|
|
leff |
|
|
|
|
leff |
i |
|
dt |
|
|
i |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
||||||||
Получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
K |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вторым членом |
leff |
можно пренебречь, так как он является членом второго порядка |
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
K |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
малости относительно leff |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
dCi |
|
|
d |
Ci0 Ci |
|
i |
N |
0 N i Ci0 Ci ; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Аналогично запишем (2): |
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
leff |
(5) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из уравнения (5) исключим члены, описывающие стационарное состояние реактора: и остальное преобразуем по Лапласу при нулевых начальных условиях:
|
N |
0 |
6 |
|
|
i |
|
|
p N p |
|
K p p Ci |
p ; |
p Ci |
N p i Ci p ; |
|||
leff |
||||||||
|
||||||||
|
i |
|
(7) |
leff |
||||
|
|
|
|
|
|
|
||
(8)
Комбинируя (7) и (8), получаем:
|
|
N0 |
|
|
6 |
|
i |
|
|
|
|
|
6 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
p |
|
|
|
|
p 1 |
|
|
|
|
|
N p |
||||||
p N p |
|
|
K p |
|
|
p |
|
|
N p ; |
|
p |
|
|
|||||
|
|
leff |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
i |
l |
i |
|
|
i |
l |
i |
|
|||||||
|
|
|
|
|
|
eff |
|
|
|
|
или: |
|
eff |
|
|
|
||
N 0 K p ; leff
Окончательно |
получаем |
ПЕРЕДАТОЧНУЮ |
Wr p |
N |
p |
N0 |
|
|
|
|
1 |
|
|
|
|
K |
l |
|
|
|
|
|
|
|
|
|
|||||
ФУНКЦИЮ |
РЕАКТОРА |
В ТОЧЕЧНОМ |
|
|
|
eff |
|
|
6 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ПРИБЛИЖЕНИИ в виде: |
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
||||||
|
|
|
|
|
|
|
|
|
i l |
eff |
i |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

1.11Определение передаточной функции ЯР по уравнениям точечной кинетики. Частотные характеристики элементарного реактора.
|
dN |
|
K N |
6 |
|
|
|
|
dC |
i |
|
|
i |
N iCi ; |
|
||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
iCi ; |
|
|
|
|
|
||||||||||
|
|
|
|
dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
dt |
|
leff |
i |
|
|
(1) |
|
|
|
leff |
(2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выразим из уравнения (2) i Ci и подставим в (1): |
|
|
|
|
|
||||||||||||
|
|
|
|
dN |
|
K |
6 dCi |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
leff |
|
dt |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
i |
|
|
|
(3) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Представим N в виде суммы двух слагаемых: N0 – стационарной величины и δN – малого отклонения. Таким же образом представим Ci в виде суммы Ci0 и δCi.В уравнение (3)
подставим новые переменные N N0 N; Ci Ci0 Ci ;
|
dN |
|
d |
|
|
K |
|
|
|
|
K |
6 |
d |
|
|
|
|
|
|
|
|
N |
|
|
N |
0 |
|
|
N |
|
|
C ; |
|
|
|
|
|
|
|
|
|
|
||||||||
|
dt |
|
dt |
|
|
leff |
|
|
|
leff |
i |
dt |
|
i |
||
|
|
|
|
|
|
|
|
(4) |
||||||||
Получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
K |
N |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вторым членом |
|
leff |
|
можно |
пренебречь, так как он является членом второго |
|||||||||||
|
|
|
|
|
||||||||||||
K N
порядка малости относительно leff Аналогично уравнение (2) запишем в виде:
|
|
|
|
dCi |
|
|
|
d |
Ci0 Ci |
|
i |
N 0 N i Ci0 Ci ; |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
leff |
|
|
|
|
|
|
|
|
|
(5) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Из уравнения (5) исключим члены, описывающие стационарное состояние реактора: |
||||||||||||||||||||||||||||||
и остальное преобразуем по Лапласу при нулевых начальных условиях: |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
N |
0 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|||||
p N p |
|
|
K p p Ci p ; |
|
|
|
p Ci |
|
N p i Ci p ; |
||||||||||||||||||||||
leff |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
(7) |
|
|
|
|
leff |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комбинируя (7) и (8), получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
N0 |
|
|
|
|
|
6 |
|
i |
|
|
|
|
|
|
6 |
|
|
i |
|
|
|
N 0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
p N p |
|
|
|
|
|
K p |
|
|
|
p |
|
|
|
|
N p ; |
p 1 |
|
|
|
|
|
|
N p |
|
K p ; |
||||||
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|||||||||||||||||
|
|
|
leff |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
leff |
|
|||||||
|
|
|
|
|
|
|
|
|
|
i l |
|
|
или: |
|
i |
l |
|
i |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eff |
i |
|
|
|
|
|
|
eff |
|
|
|
|
|
||||
Окончательно получаем ПЕРЕДАТОЧНУЮ ФУНКЦИЮ РЕАКТОРА В ТОЧЕЧНОМ ПРИБЛИЖЕНИИ в виде:
Wr p |
N |
p |
N0 |
|
|
|
|
1 |
|
|
|
|
K |
l |
|
|
|
|
|
i |
|
|
|
||
|
|
|
eff |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
||||
|
|
|
|
|
|
i l |
eff |
i |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТАРНОГО ЯДЕРНОГО РЕАКТОРА
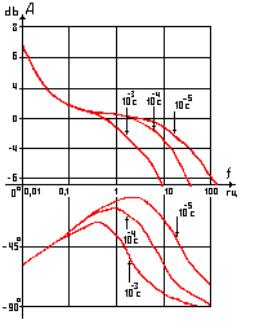
Логарифмические частотные характеристики построены для разных значений эффективного времени жизни нейтронов leff. Как видно из графика, АЧХ на низких частотах не зависит от времени жизни мгновенных нейтронов, а в области частот начиная с 1 герца частотный диапазон для быстрых реакторов становится больше. ФЧХ также начинает различаться для разных типов реакторов, начиная с частот входных сигналов реактивности около 1 герца. Максимальный фазовый сдвиг находится в пределах 100 – 110 градусов. Видно, что элементарный физический реактор является неустойчивым астатическим объектом регулирования, на низких частотах входных сигналов амплитудно-частотная характеристика устремляется в бесконечность.

1.12 Получение передаточной функции ЯР по уравнениям точечной кинетики. Особенности передаточной функции ЯР.
|
|
|
|
6 |
|
dC |
i |
|
|
i |
|
|
|
|
|
|
|
|
|
dN |
|
K N iCi ; |
|
|
|
|
N iCi |
; |
|
|
|
|
|
|
|||
|
|
|
dt |
|
|
|
|
|
K |
6 dCi |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
dt |
|
leff |
i |
(1) |
|
|
leff |
(2) |
dN |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
dt |
leff |
dt |
|||||
|
|
|
|
C |
|
|
|
|
|
|
|
i |
||||||
Выразим из уравнения (2) |
i i и подставим в (1): |
|
|
|
|
|
(3) |
|||||||||||
Представим N в виде суммы двух слагаемых: N0 – стационарной величины и δN – малого отклонения. Таким же образом представим Ci в виде суммы Ci0 и δCi.В уравнение (3)
подставим новые переменные N N0 N; Ci Ci0 Ci ;
|
dN |
|
|
d |
|
|
|
|
K |
|
|
|
|
|
K |
6 |
|
d |
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
N |
0 |
|
|
N |
|
|
|
C ; |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dt |
|
|
dt |
|
|
|
leff |
|
|
|
|
leff |
i |
|
dt |
|
|
i |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
||||||||
Получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
K |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вторым членом |
leff |
можно пренебречь, так как он является членом второго порядка |
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
K |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
малости относительно leff |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
dCi |
|
|
d |
Ci0 Ci |
|
i |
N |
0 N i Ci0 Ci ; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Аналогично запишем (2): |
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
leff |
(5) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из уравнения (5) исключим члены, описывающие стационарное состояние реактора: и остальное преобразуем по Лапласу при нулевых начальных условиях:
|
N |
0 |
6 |
|
|
i |
|
|
p N p |
|
K p p Ci |
p ; |
p Ci |
N p i Ci p ; |
|||
leff |
||||||||
|
||||||||
|
i |
|
(7) |
leff |
||||
|
|
|
|
|
|
|
||
(8) |
|
|
|
|
|
|
|
|
Комбинируя (7) и (8), получаем: |
|
|
|
|
||||
|
|
N0 |
|
|
6 |
|
i |
|
|
|
|
|
6 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
p |
|
|
|
|
p 1 |
|
|
|
|
|
N p |
||||||
p N p |
|
|
K p |
|
|
p |
|
|
N p ; |
|
p |
|
|
|||||
|
|
leff |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
i |
l |
i |
|
|
i |
l |
i |
|
|||||||
|
|
|
|
|
|
eff |
|
|
|
|
или: |
|
eff |
|
|
|
||
N 0 K p ; leff
Окончательно |
получаем |
ПЕРЕДАТОЧНУЮ |
|
N |
|
N0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
ФУНКЦИЮ |
РЕАКТОРА |
В |
ТОЧЕЧНОМ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Wr |
p K p l |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ПРИБЛИЖЕНИИ в виде: |
|
|
|
|
|
|
|
|
|
i |
|
|
|||||||||||
Основное |
свойство выведенной |
передаточной |
|
|
|
eff |
|
|
|
6 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
p 1 |
|
|
p |
|
|
|
||||||||||||
функции |
реактора состоит |
в том, |
что она не |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
i l |
eff |
i |
|
|||||||||||
линейна, то есть коэффициент передачи реактора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
как элемента системы регулирования зависит от мощности, на которой он работает. Это |
|
|
|
|
|
||||||||||||||||||
недопустимо, с точки зрения управления, так как на малых уровнях мощности реактор, а также и |
|
|
|
|
|
||||||||||||||||||
замкнутый контур регулирования, будут иметь малую величину коэффициента передачи, а на |
|
|
|
|
|
||||||||||||||||||
больших уровнях мощности этот коэффициент вырастет и система регулирования потеряет |
|
|
|
|
|
||||||||||||||||||
показатели качества, на которые она была настроена, или станет неустойчивой. => эта |
|
|
|
|
|
||||||||||||||||||
зависимость коэффициента усиления реактора от мощности необходимо устранить при |
|
|
|
|
|
||||||||||||||||||
проектировании системы. Часто это делают так, чтобы коэффициент усиления регулятора был |
|
|
|
|
|
||||||||||||||||||
обратно пропорционален мощности. Так как эта особенность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
снимается при проектировании регулятора, то в расчетах |
|
|
|
|
|
N |
|
p Kr T1 p 1 . |
|||||||||||||||
передаточную функцию реактора берут в относительном виде: |
W p |
|
|
N0 |
|
||||||||||||||||||
|
|
|
|
|
|
|
r |
|
|
K |
|
|
|
|
|
p T2 p 1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1.13 Динамика реактора с учетом контура обратной связи по температуре. Передаточная функция контура внутренней температурной обратной связи. Частотные характеристики ЯР с учетом Ктс.
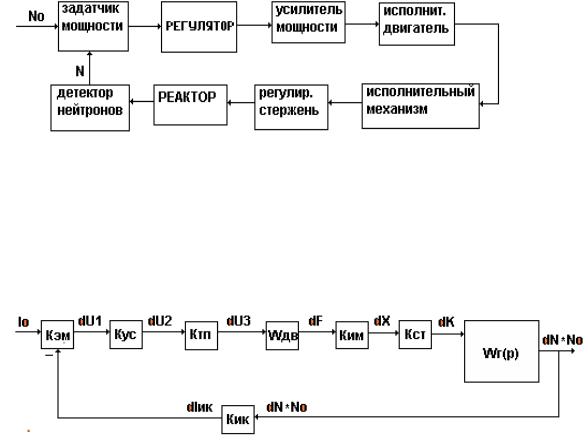
Регулируемый объект в этом случае можно представить следующей структурной схемой:
Wr(p) – передаточная функция элементарного реактора нулевой мощности, Wtc(p) – передаточная функция температурного коэффициента реактивности.
Передаточная функция температурной обратной связи по реактивности:
Wtc p |
K |
p |
A * B |
|
|
Ktc |
|
. |
N |
Ttc p |
|
Ttc p 1 |
|||||
|
|
1 |
|
|||||
δК |
N |
|
Wr(p) |
δN |
|
|
|
||
|
|
|
|
|
|
|
|
|
Wtc(p) |
|
|
Wr p |
|
|
|
|
Wrtc p |
|
|
. |
||
1 W |
p W |
p |
|||
|
r |
|
tc |
|
|
Тогда передаточная функция реактора с учетом обратной связи по Ktc принимает вид: Стабилизирующий эффект температурной обратной связи по реактивности можно
получить, определяя значение передаточной функции Wrtc(p) на нулевой частоте. |
||||||
Пренебрегая членами с Тtc ввиду малости постоянной времени, имеем: |
||||||
Wrtc p |
Wr p 1 Ttc |
|
Wr p |
|
1 |
. |
|
|
Ktc |
||||
1 Ttc p KtcWr p |
1 KtcWr p |
|
|
|||
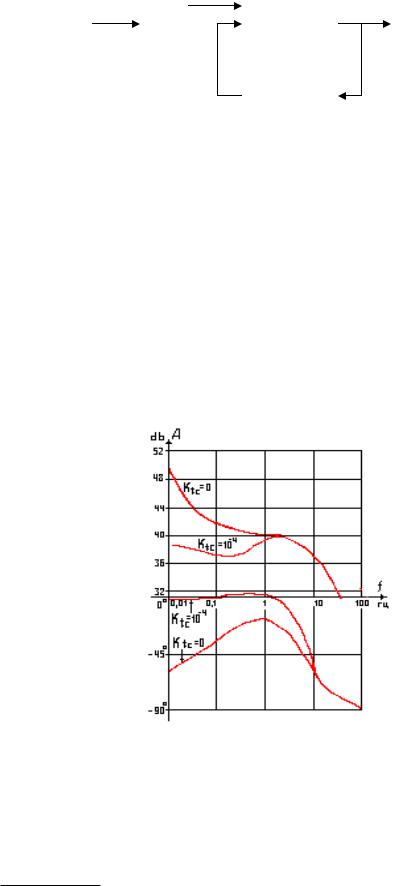
=>, реактор с учетом внутреннего контура тепловой обратной связи является статическим, устойчивым объектом, и его коэффициент передачи на нижних частотах обратно пропорционален величине усредненного температурного коэффициента реактивности.
На очень низких частотах передаточная функция определяется только обратной связью Ktc. Коэффициент усиления реактора уже не растет до бесконечности, а состав-
ляет некоторую конечную величину ≈ 1 / Ktc. Величина фазового сдвига становится близкой нулю. Величина этого опережения выходного сигнала по фазе зависит от величины Тtc. На высших же частотах характер ЛАЧХ и ЛФЧХ практически не изменился и определяется временем жизни нейтронов, как и в элементарном реакторе.
Коэффициент усиления контура обратной связи по Ktc пропорционален уровню мощности. По мере снижения мощности влияние внутреннего контура тепловой
обратной связи падает, так что на нижних уровнях мощности реактор труднее поддается регулированию, чем на больших. Ввиду этого диапазон автоматического регулирования обычно ограничен двумя декадами, т.е. от 1 до 100 % NПОТ. В этом диапазоне при проектировании системы регулирования передаточная функция реактора может быть взята в относительном виде:
Wr p

1.14 Динамика ЯР с учетом контура обратной связи по отравлению. Ксеноновые колебания мощности, их причина и устранение.
Всю систему можно рассмотреть в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
комплекса |
|
обратных |
|
связей, |
|
|
|
охватывающих |
|
dK |
|
|
|
|
|
|
|
Wrtc(p) |
|
|
|
dN |
||||||||||||||||||||||||
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
передаточную функцию ядерного реактора. Контур |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
обратной связи по отравлению можно представить, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
dK |
|
|
|
dX |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
как произведение |
|
передаточной |
функции |
dN |
на |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dX |
|
|
|
dN |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dK |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
коэффициент передачи |
dX |
|
производящий перевод |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
отравления в величину реактивности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х-концентрация |
ксенона, γy- парциальный |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
X |
|
p |
|
|
|
y y |
|
|
|
|
|
|
выход йода, γх- парциальный выход ксенона, |
|||||||||||||||||||||||||||
X |
|
|
x |
|
|
x |
|
0 |
x x X 0 |
|
y |
|
|
σх |
|
– |
сечение |
поглощения |
|
тепловых |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
N p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
нейтронов |
для ксенона. λх – |
Постоянная |
||||||||||||||||||||||||||
|
|
|
|
p |
p |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
x |
|
0 |
|
x |
|
|
|
|
распада ксенона, |
λх |
– Постоянная распада |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
йода |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношение между |
X 0 и |
|
N 0 в общем виде определяется из |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
уравнения |
|
для |
|
|
равновесной |
|
|
концентрации |
отравления: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
X 0 |
x |
|
|
y |
N |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x x N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рассмотрим динамику реактора, охваченного контуром обратной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
связи |
по |
|
отравлению. |
Предположим, |
|
что |
реактор обладает |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
отрицательным температурным коэффициентом реактивности. Рассмотрим это с помощью логарифмических частотных характеристик. Влияние контура по отравлению сказывается на очень низких частотах порядка 10–7 ÷ 10–3 гц. В этом частотном диапазоне ЛАЧХ реактора с учетом Ktc имеет вид прямой, параллельной оси частот с коэффициентом передачи ≈ 1 / Ktc. ЛФЧХ такого реактора также идет параллельно оси частот с фазовым сдвигом, равным 0 градусов.
Для устойчивости системы необходимо, чтобы модуль передаточной функции системы в разомкнутом состоянии был меньше единицы, когда фазовый сдвиг составляет
– 180 градусов (другими словами фазовый сдвиг на частоте среза должен быть меньше – 180 градусов). Передаточная функция реактора с
учетом Ktc и отравления на низких частотах
|
1 |
W |
|
p |
|
|
|
Xe |
|||
указанного диапазона будет иметь вид Ktc |
. |
||||
|
|||||
Поэтому, устойчивость реактора будет зависеть от величины Ktc. Для каждого конкретного уровня потока нейтронов существует предельное значение Ktc, выше которого система устойчива, а ниже – неустойчива.
При потоках больше 3·1011 для
поддержания устойчивости надо, чтобы величина Ktc превышала определенную величину, максимум которой находится при потоке около 1013 [н / см2 · c]. При дальнейшем
|
1 |
W |
|
p |
|
|
|
Xe |
|||
увеличении потока амплитуда передаточной функции |
Ktc |
уменьшается и для |
|||
|
|||||
поддержания устойчивости достаточен небольшой отрицательный Ktc.
Некоторые из вторичных изотопов (ксенон и самарий), образующихся при распаде ядер урана, имеют большие сечения поглощения нейтронов и поэтому действуют как вредные поглотители.
КСЕНОНОВЫЕ КОЛЕБАНИЯ – периодические колебания мощности реактора, вызванные неустойчивостью контура внутренней обратной связи реактора по отравлению ксеноном. Особой опасности эти проявления неустойчивости не представляют. Они возникают из-за фазовой неустойчивости в очень низком диапазоне частот (1 – 2 колебания в сутки). Поэтому, периодически перемещая стержни управления, оператор справляется с этими колебаниями. По этой причине ксеноновые колебания не учитываются при проектировании системы автоматического регулирования мощности.
Подавление ксеноновых колебаний превращается в сложную задачу управления лишь в больших канальных реакторах, в которых из-за нестабильности нейтронного поля в центре активной зоны наблюдаются большие различия в уровне равновесного отравления в различных частях активной зоны.

1.15.Определение передаточной функции контура отравления ЯР. Причина ксеноновых колебаний мощности.
|
|
dY |
|
-уравнения концентраций йода и ксенона. |
|
|
|||||
|
|
|
|
y N yY; |
Х-концентрация ксенона, γy ,γх - парциальный выход йода и ксенона, |
||||||
|
|
dt |
|||||||||
|
dX |
|
σх – |
сечение |
поглощения |
тепловых |
нейтронов |
для |
|||
|
|
x x X N |
yY x X ; |
|
|
|
|
|
|
||
|
dt |
ксенона. |
λх – |
Постоянная |
распада ксенона, λх |
– |
|||||
|
|
|
|
|
|
||||||
Постоянная распада йода. |
|
|
|
|
|
|
|||||
|
Линеаризуем методом малых отклонений: X X0 X Y Y0 Y N N0 |
N; |
|
||||||||
dtd X0 X x x X0 N0 x x X0 N x N0 x X yY0 y Y x X0;
где величиной x N X пренебрегли ввиду ее малости. исключаем члены, описывающие установившийся режим
|
d |
X |
|
Y |
|
|
|
X |
|
N |
N |
|
|
|
X . |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dt |
y |
|
|
|
|
x |
|
|
x |
|
0 |
|
|
x |
|
0 |
|
x |
|
|
|
|
|
|
|
|
|
|||||
Аналогичным образом преобразуем уравнение (1): |
|
|
|||||||||||||||||||||||||||||||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|||
|
|
|
Y0 Y |
y N0 y N yY0 y Y. |
|
|
|
|
|
|
|
|
Y y N y Y. |
||||||||||||||||||||
|
|
dt |
|
|
|
|
|
|
|
dt |
|||||||||||||||||||||||
Приводим к операторному виду с помощью преобразования Лапласа: |
|||||||||||||||||||||||||||||||||
|
p X p |
y |
|
|
|
x |
|
|
x |
|
0 |
|
|
|
x |
|
0 |
|
x |
|
|
|
|||||||||||
|
|
|
Y p |
|
|
|
|
X |
|
N p |
|
|
N |
|
|
|
|
X p ; |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y p |
|
y |
|
N p ; |
|||||
|
p Y p |
|
|
N p |
|
Y p ; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
y |
y |
|
|
|
|
|
|
|
p |
y |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражаем : |
|
|
|
|
|
|
|
|
|
и подставляем в первое: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
X p
Выраж.
y y N p x x X 0 N p x N |
0 x X p ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
p y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
p |
|
|
y |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
x |
x |
0 |
|
|
|
|
|
|
|
|
|||||||||||||||
X |
|
y |
y |
p |
|
x |
x |
0 |
X |
|
|
|
|
|
|
x x X 0 |
|
y |
|
||||||||||||||||||||||
p |
|
|
|
|
y |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
N |
|
|
|
|
|
p |
|
N |
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
p |
|
N |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
p |
|
x |
0 |
x |
|
|
|
|
|
|
|
p |
|
|
x |
0 |
x |
|
|
|||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Некоторые из вторичных изотопов (ксенон и самарий), образующихся при распаде ядер урана, имеют большие сечения поглощения нейтронов и поэтому действуют как вредные поглотители.
КСЕНОНОВЫЕ КОЛЕБАНИЯ – периодические колебания мощности реактора, вызванные неустойчивостью контура внутренней обратной связи реактора по отравлению ксеноном. Они возникают из-за фазовой неустойчивости в очень низком диапазоне частот (1 – 2 колебания в сутки).
2.1 Линейная система регулирования мощности ЯР. Структура, элементы системы.
В линейной системе перемещение стержня прямо пропорционально ошибке регулирования и направлено в сторону ее уменьшения.
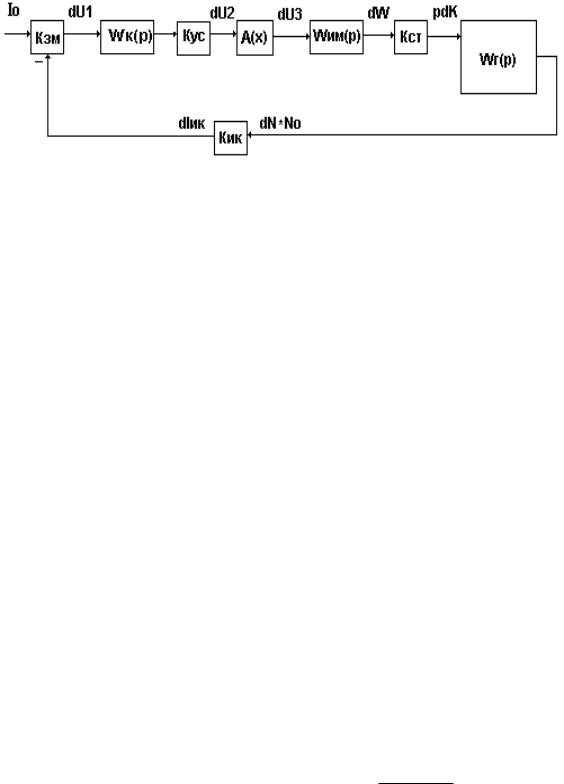
Структурная схема линейной САР мощности ядерного реактора имеет вид:
Нейтронный детектор, которым является обычно ионизационная камера, выдает сигнал, пропорциональный среднему значению потока нейтронов в активной зоне N. В сравнивающем устройстве (задатчике
мощности) происходит сравнение этого сигнала с сигналом заданной мощности N0. Затем сигнал ошибки регулирования усиливается по амплитуде усилителем сигнала ошибки, усиливается по мощности в усилителе мощности и поступает в обмотку исполнительного двигателя. Вращающийся вал двигателя через понижающий редуктор и кинематическое исполнительное устройство перемещает стержень на определенную величину в нужном направлении.
В качестве примера ограничимся пропорциональным законом регулирования. Структурная схема системы принята в виде:
1.ЗАДАТЧИК МОЩНОСТИ часто выполняет в системе две функции. Во-первых: он выдает разностный сигнал ошибки, во-вторых: он используется для устранения
dU |
|
|
K3m |
dI |
|
; |
1 |
|
ik |
||||
нелинейности ядерного реактора. |
|
N0 |
т.е. учитываем, что K3m обратно |
|||
|
|
|
||||
пропорционален N 0 .
2.Усилитель сигнала ошибки регулятора: dU 2 K yc dU 1. Выбор величины K yc производят, исходя из требований точности регулирования, учитывая величину напряжения трогания двигателя.
3.Тиристорный преобразователь: dU3 KtpdU2 . Малой инерционностью преобразователя можно пренебречь.
|
|
d p |
|
Kdv |
|
|
|
|
|
|
|
|
; |
|
|
|
|
4. |
Двигатель: |
|
p Tdv p 1 |
5. Исполнительный механизм: dX Kumd . |
||||
6. |
Управляющий стержень: dK Kct dX . |
|||||||
7. |
Ядерный |
реактор |
без учета |
температурных обратных связей c учетом одной |
||||
|
|
|
|
|
|
|
Kr T1 p 1 |
|
|
|
|
|
|
|
dN p |
|
dK p ; |
|
|
|
|
|
|
p T p 1 |
||
усредненной группы запаздывающих нейтронов: |
2 |
|
8.ДЕТЕКТОРЫ НЕЙТРОНОВ системы располагаются либо в специальных каналах в бетонной защите реактора, либо в каналах самой активной зоны: датчики внешнего контроля и датчики внутриреакторного контроля. dIik=Kik*dN*No.
2.2 Релейная система регулирования мощности ЯР. Структура, элементы системы, методы анализа.
Для регулирования мощности ядерного реактора чаще всего используется релейная система регулирования. Это вызвано следующими обстоятельствами:
–требования к точности регулирования мощности на энергетических, экспериментальных и транспортных реакторах невысоки;
–релейный привод является более простым и менее энергоёмким по сравнению с линейным;
–малая чувствительность к шумам детектора нейтронов, особенно чувствующаяся на малых уровнях мощности.
Наличие зоны нечувствительнос ти реле приводит к возможности возникновения автоколебательно го режима при неточной
настройке регулятора. Поэтому, необходимо чтобы реактор был устойчивым объектом управления, то есть обладал свойством самовыравнивания, что возможно только при отрицательном температурном эффекте реактора.
Фазовый компенсатор Wk(p) используется для компенсации фазовой неустойчивости системы, т.е. устранения возможных автоколебаний.
Релейный элемент A(x) представляет собой одно или несколько реле с двумя группами контактов. Контакты реле замыкаются, когда сигнал ошибки превышает некоторую заданную величину, и отпускают, когда сигнал ошибки станет меньше другой заданной величины. При изменении знака рассогласования замыкается и размыкается другая группа контактов реле. Эти контакты управляют направлением вращения двигателя и выключают его, когда ошибка становится ниже уровня зоны нечувствительности. Принимается, что двигатель вращается с постоянной скоростью dw и изменение
реактивности на входе реактора происходит с постоянной скоростью p K .
1.ЗАДАТЧИК МОЩНОСТИ часто выполняет в системе две функции. Во-первых: он
выдает разностный сигнал ошибки, во-вторых: |
он |
используется |
для устранения |
||||||
dU |
|
|
|
K3m |
dI |
|
; |
|
|
1 |
|
|
ik |
|
|
||||
нелинейности ядерного реактора. |
|
|
N0 |
т.е. |
учитываем, |
что K3m обратно |
|||
|
|
|
|
||||||
пропорционален N 0 . |
|
|
|
|
|
|
|
|
|
2. Усилитель сигнала ошибки регулятора: |
dU |
2 K yc dU 1. |
|
|
|||||
|
|
|
|
|
|
|
|
||
Передаточные функции реактора и двигателя необходимо видоизменить.
3. Так как скорость вращения двигателя в релейной системе постоянна, то передаточная
|
Wdv p |
w |
p |
|
Kdv |
|
. |
|
функция двигателя теряет свой астатизм: |
Udv |
Tdv p 1 |
||||||
|
|
|
||||||
4. Так как входной величиной в реакторе |
является уже не |
реактивность, а скороcть ее |
||||||
изменения, то порядок астатизма передаточной |
функции элементарного реактора |
|||||||
|
Wr p |
dN / N0 |
p |
|
увеличивается до второго: |
p K |
|||
|
|
|||
|
|
|
5. Исполнительный механизм: dX Kumd .
Kr T1 p 1 .
p2 T2 p 1
6. Управляющий стержень: dK Kct dX .
