Файловый архив студентов. Файловый архив студентов.
1259 вузов, 4592 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Томский Политехнический Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Ответы Корначук СК71

.pdf
Скачиваний:
139
Добавлен:
25.03.2016
Размер:
1.18 Mб
Скачать
☆

1.1 Типы ЯР по назначению. Особенности систем управления мощностью различных типов ЯР.

По назначению используются ректоры следующих видов:

—исследовательские и материаловедческие;

—транспортные;

—промышленные (размножители ядерного топлива);

—энергетические.

ИССЛЕДОВАТЕЛЬСКИЕ И МАТЕРИАЛОВЕДЧЕСКИЕ РЕАКТОРЫ предназначены для

проведения исследовательских работ в различных отраслях промышленности. Система управления мощностью исследовательских реакторов имеет следующие особенности: необходимо иметь возможность многократно останавливать и пускать реактор в течении суток в соответствии с программой научных исследований. Поэтому пуск реактора происходит в автоматическом режиме в течении нескольких минут, а запас реактивности на стержнях управления является достаточным для подавления эффекта ксенонового отравления.

ТРАНСПОРТНЫЕ РЕАКТОРЫ надводных, подводных и космических объектов должны обеспечивать высокую маневренность этих объектов. В связи с этим системы управления транспортных реакторов систем обладают большим запасом реактивности для возможности включения реактора в любое желаемое время после остановки, а также имеют конструктивные особенности привода и управляющих органов для работы в условиях вибрации, качки. Транспортные реакторы имеют практически такую же систему управления как и исследовательские.

Промышленные реакторы предназначены для работы на постоянном высоком уровне мощности как можно дольше с целью получения большего количества Pu-239. Поэтому основная задача системы управления здесь: поддержание постоянным высокого уровня мощности без частых непредвиденных остановок. Для предотвращения случайных остановок предусматривают специальные меры: большое количество дублирующих приборов, 3-х кратное резервирование всего контура автоматического регулирования и т.д.

Энергетические реакторы предназначены для получения тепловой и электрической энергии. Здесь задача управления определяется программой работы электрической станции в пиковом или базовом режиме. Как правило, не требуется длительная работа реактора на максимальном уровне мощности, но предотвращение случайных остановок реактора является необходимым условием. Поэтому усиленное внимание уделяется надежности систем контроля и аварийной защиты. Кроме того, необходимость увеличивать мощность реакторного блока до 1000 и более мегаватт для снижения себестоимости электроэнергии приводит к увеличению размеров активной зоны и необходимости принимать специальные меры для стабилизации распределения мощности по объему активной зоны. Поэтому система управления мощностью энергетического реактора является наиболее сложной.

1.2 Модель кинетики ЯР в точечном приближении. Уравнения модели, роль запаздывающих нейтронов. Область применения модели.

Пусть N – число нейтронов данного поколения. N+δk – число нейтронов следующего поколения. Тогда уравнение прироста нейтронов запишется:

 

 

K

 

 

 

 

 

 

K

t

 

dN

 

 

dN

 

K

 

 

 

 

N ;

 

Ndt;

 

l

 

 

 

 

 

 

 

 

 

 

 

dt

 

l

 

N

 

l

 

N N e

eff

;

 

 

 

eff

 

 

 

eff

 

0

 

 

N0 – число нейтронов в начальный момент.

 

 

 

 

 

 

 

 

 

 

Таким образом мы можем представить ядерный реактор в точечном приближении как объект управления:

 

 

 

δK

 

 

 

 

N

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

Часто выходной управляемой величиной может служить не

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

плотность нейтронов, а период реактора:

 

 

 

T

 

1

 

 

;

 

 

 

1 1 dN

 

d

 

 

 

 

 

 

 

 

 

 

 

 

1 dN

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ln N ; T- период реактора.

 

 

 

 

 

 

 

 

 

 

Практически всегда измеряется:

T

N

 

dt

dt

 

 

 

N dt

 

 

Период реатора – время, в течение которого мощность реактора изменяется в e = 2,7 раз. Не все нейтроны испускаются мгновенно, небольшая часть испускается через некоторое время осколками деления. Эти нейтроны играют важную роль при управлении ядерной реакцией деления. С учетом запаздывающих нейтронов уравнение кинетики реактора приводится к следующему виду:

dN

 

K

 

 

6

 

dC

 

 

 

 

 

N

N C ;

i

 

 

i

N

C ;

 

 

 

 

 

 

dt leff

leff

i

i i

dt

leff

i i

 

 

где Ci — концентрация ядер — носителей i й группы запаздывающих нейтронов, i - постоянная распада. i - доля от общего числа нейтронов.

K

N

 

 

leff

-

изменение N за счет мгновенных нейтронов данного поколения ;

 

 

 

 

N

 

 

 

 

 

leff

-

изменение N за счет запаздывающих нейтронов данного поколения ;

 

 

 

6

i Ci

i - изменение N за счет запаздывающих нейтронов предыдущих поколений.

Модель точечного реактора лежит в основе всех расчетов по проектированию систем управления реакторов.

Упрощенная модель с учетом одной усредненной группы запаздывающих нейтронов

 

dN

 

K

N

 

N C;

dC

 

 

N C;

 

dt

l

l

dt

l

 

 

 

 

 

 

запишется:

 

 

eff

 

eff

 

 

 

eff

 

 

 

 

 

 

 

 

 

 

 

В надкритическом режиме запаздывающие нейтроны резко снижают рост мощности реатора. Коэффициент размножения определяет возможность поддержания цепной реакции: K = число нейтронов данного поколения / число нейтронов предыдущего поколения;(критика, подкритика, надкритика) K = образование нейтронов/ поглощение

Для реакторов конечных размеров Kэфф = образование нейтронов /

 

Keff

1

(утечка+поглощение).

K

 

 

;

 

 

Реактивность(мера отлонения реатора от критического состояния) :

 

Keff

lэфф - время жизни нейтронов в реакторе конечных размеров. Время

leff

 

l

 

K

 

 

между образованием нейтрона и его выходом из активной зоны в процессе поглощения или утечки.

1.3 Уравнения точечной кинетики ЯР: для мгновенных нейтронов, для 6-и групп запаздывающих нейтронов, для одной усредненной группы.

N – число нейтронов данного поколения. N+δk – число нейтронов следующего поколения

dN

 

K

N ;

dt

l

 

 

 

 

eff

- для мгноновенных нейтронов.

 

 

 

Учет запаздывающих нейтронов в уравнении кинетики реактора приводит его к следующему виду:

dN

 

K

 

 

6

dCi

 

i

 

 

N

N i Ci ;

 

N i Ci ;

 

 

leff

 

 

 

 

dt

 

leff

i

dt

leff

Ci - концентрация ядер - носителей i й группы запаздывающих нейтронов, i - постоянная распада. i - доля от общего числа нейтронов

Упрощенная модель кинетики с учетом одной усредненной группы запаздывающих нейтронов выглядит следующим образом:

dN

 

K

N

 

N C;

dC

 

 

N C;

 

 

 

 

 

dt

 

leff

leff

 

dt

 

leff

 

где

K

 

K

 

N

 

 

 

 

leff

 

 

 

 

– изменение N за счет мгновенных нейтронов данного поколения;

 

 

 

 

 

 

 

N

 

 

 

 

leff

 

 

 

 

– изменение N за счет запаздывающих нейтронов данного поколения;

 

 

 

 

6

 

 

 

 

 

C

 

i

i i – изменение N за счет запаздывающих нейтронов предыдущих поколений.

lэфф - время жизни нейтронов в реакторе конечных размеров.

Реактивность - мера отлонения реатора от критического состояния

Keff 1 ; Keff

1.4 Понятие реактивности. Избыточная и остаточная реактивности. Определение запаса реактивности на стержнях управления.

РЕАКТИВНОСТЬ – это мера отклонения реактора от критического состояния.

K

Keff

1

;

Keff

 

 

(>,=,<0-разгон, крит. сост., спад

Определяется выражением:

 

 

мощности)

Реактивность определяет изменение скорости протекания цепной реакции в установившемся режиме.

Реактор, спроектированный так, что коэффициент размножения в точности равен единице, был бы неработоспособен, так как разогрев его при выходе на мощность, а также потеря реактивности за счет отравления ксеноном сделали бы его глубоко подкритичным. Поэтому коэффициент размножения рассчитывается несколько большим единицы, а затем путем частичного введения поглощающих стержней реактивность уменьшается до критического состояния.

Величина Кэфф – 1 = δΚизб при полностью выведенных стержнях управления называется избыточной реактивностью.

Величина δΚ – 1 = δΚост при полностью погруженных стержнях управления называется остаточной реактивностью.

Для нормальной работы нам необходимы стержни с эффективностью 28 % запаса реактивности. Единицы измерения запаса реактивности могут быть в процентах реактивности или в относительных единицах. На производстве часто измеряют запас реактивности в "стержнях" или "линейных метрах". Если известна суммарная избыточная реактивность, то величину линейного метра реактивности вычисляют, поделив δΚизб на общую длину всех управляющих стержней. Тогда запас реактивности определяют, умножая общую непогружённую длину всех стержней на величину линейного метра реактивности. Конечно для каждого реактора цена линейного метра реактивности будет различной.

1.5 Понятия мощностного и температурного коэффициентов реактивности ЯР.

Это одна из основных причин перемещения стержней. Температура по мере разогрева реактора сильно изменяет его реактивность. Это связано с:

-размеры и физические характеристики (например, плотность урана, графита, воды) изменяются с температурой;

-поглощающие и рассеивающие свойства материалов активной зоны изменяются в зависимости от формы спектра тепловых нейтронов, который меняется под действием температуры.

Его можно учесть в виде двух коэффициентов, численные значения которых сильно меняются в зависимости от типа реактора:

1.температурного коэффициента реактивности урана; 2.температурного коэффициента реактивности замедлителя (графита или воды).

Суммарное влияние этих двух коэффициентов на мощность реактора определяет понятие КОНТУР ТЕПЛОВОЙ ВНУТРЕННЕЙ ОБРАТНОЙ СВЯЗИ реактора.

Все построенные реакторы обладают отрицательным коэффициентом тепловой обратной связи, или иначе, обладают ОТРИЦАТЕЛЬНЫМ ТЕМПЕРАТУРНЫМ

КОЭФФИЦИЕНТОМ РЕАКТИВНОСТИ. Это значит, что при нагреве реактора реактивность уменьшается. Численное значение суммарного коэффициента реактивности составляет величину от 10 5 10 4 (1/град С). Например, для реактора ВВЭР-1000 он равен 10-4, то есть при разогреве реактора на 30 градусов его реактивность уменьшается на 0.003. Значит при проектировании системы управления надо предусмотреть резерв реактивности, чтобы скомпенсировать ее потери при переходе реактора из холодного состояния в горячее.

Например, реактор, работающий на постоянном уровне мощности имеет суммарный отрицательный коэффициент реактивности. Произошло уменьшение тепловой нагрузки вторичного контура. За счет уменьшения теплоотдачи начинается увеличение температуры воды в реакторе, что вносит отрицательную реактивность и мощность реактора начинает падать. При этом происходит уменьшение температуры топлива и вносится положительная реактивность. Происходит компенсация отрицательной реактивности и мощность начинает расти. Но процесс увеличения температуры воды продолжается, вызывая падение реактивности. В результате колебательного процесса устанавливается новый уровень мощности, соответствующий новому уровню тепловой нагрузки второго контура.

Внесение положительной реактивности за счет падения температуры топлива называют МОЩНОСТНЫМ КОЭФФИЦИЕНТОМ РЕАКТИВНОСТИ.

1.6 Управляющие стержни ЯР. Градуировочная характеристика, интегральная и дифференциальная эффективность стержней. Понятие запаса реактивности.

УПРАВЛЯЮЩИЕ СТЕРЖНИ реактора имеют разное назначение. Стержни, предназначенные для аварийной остановки реактора, называют стержнями аварийной защиты (стержни АЗ). Стержни, служащие для грубой регулировки мощности с пульта оператора, называют стержнями ручной регулировки (стержни РР) или компенсирующими. Стержни, с помощью которых производится точная регулировка мощности в автоматическом режиме, без участия оператора, называют регулирующими (стержни АР).

Реактивность изменяется по нелинейному закону при изменении положения стержня, так как градуиро-

вочная характеристика стержня имеет вид:

Полная компенсирующая способность стержня, или его интегральная эффективность определяется вели-

чиной К0.

ИНТЕГРАЛЬНАЯ ЭФФЕКТИВНОСТЬ СТЕРЖНЯ определяется как его полная компенсирующая способность, равна доле реактивности, вносимой при полном погружении стержня. Не зависит от местоположения стержня в активной зоне и определяется количеством поглощающего вещества в стержне.

ДИФФЕРЕНЦИАЛЬНАЯ ЭФФЕКТИВНОСТЬ СТЕРЖНЯ определяется тангенсом

tg K

угла наклона градуировочной характеристики X и различна при разной глубине погружения стержня в активную зону. В начале погружения и в его конце эффективность стержня незначительна и является наибольшей в линейной части градуировочной характеристики. Это соответствует погружению в активную зону половины длины стержня. Именно эта максимальная дифференциальная эффективность определяется как коэффициент передачи стержня в системе автоматического регулирования мощности реактора. Дифференциальная эффективность стержня сильно зависит от его местоположения в реакторе. Стержни, расположенные в центре активной зоны имеют максимальную эффективность, так как находятся в максимуме нейтронного потока.

Запас реактивности обеспечивает компенсацию: температурного эффекта, выгорания, отравления.

1.7 Кинетика ЯР при ступенчатом изменении реактивности. Анализ решения - по уравнению обратных часов.

Кинетические характеристики описывают изменение мощности реактора при определенном законе изменения реактивности.

Рассмотрим кинетику реактора в точечном приближении, пренебрегая пространственными эффектами. Считаем также, что температурные эффекты и эффект отравления равны нулю, то есть реактор является реактором нулевой мощности.

Кинетика при ступенчатом изменении реактивности характеризует работу реактора при резком изменении мощности в результате действий оператора при переходе на новый уровень или в результате действия системы аварийной защиты при сбросе мощности.

 

 

 

 

6

 

dC

i

 

 

i

 

 

dN

 

K N iCi

;

 

 

 

N iCi ;

 

 

dt

 

 

 

 

 

 

 

dt

 

leff

i

 

 

 

leff

Решение уравнений точечной кинетики

 

 

 

 

 

 

 

 

 

 

при ступенчатом изменении реактивности является линейной комбинацией

экспоненциальных функций. Константы wj

связаны с реактивностью характеристическим

уравнением реактора, которое называют УРАВНЕНИЕМ ОБРАТНЫХ ЧАСОВ:

Для случая K const система уравнений

является линейной и мы можем применить к

ней преобразование Лапласа. Решая систему, получаем:

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

l

 

1

 

 

i

 

 

 

 

 

 

 

 

 

 

 

l

 

p

 

 

 

 

 

 

 

 

 

eff

eff

 

 

 

 

 

A p

 

N

 

 

 

 

 

 

 

 

i

 

N0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N0 .

 

 

 

 

 

 

 

 

 

 

 

i

 

B p

 

 

 

 

p K i

 

i

 

 

 

 

 

leff

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p i

 

Приравнивая нулю знаменатель, получаем характеристическое уравнение реактора, известное под названием уравнения обратных часов:

 

p K

i i

 

 

 

 

 

6

i p

 

 

 

leff

 

0

 

K l

eff

p

p

.

 

 

 

 

 

 

i p

i

 

;

 

i

i

 

 

 

 

 

 

 

 

 

 

Все корни характеристического уравнения реактора являются действительными,

причем один из них, пусть это будет p1, по знаку совпадает со знаком возмущения реактивности, а остальные корни отрицательные.

Находя для выражения (1) оригинал с помощью обратного преобразования Лапласа, получим общий вид решения уравнений кинетики:

N t N 7 A exp p t . 0 i i i

Очевидно, при положительной реактивности корень p1 будет определять нарастание

T

 

 

1

 

p

p1 . Поэтому, если подставить значение p1 в уравнение

 

 

мощности с периодом

 

 

обратных часов, то получим соотношение, связывающее реактивность и период реактора:

 

l

6

 

i

 

K

eff

 

 

.

Tp

1 i Tp

 

i

 

При малых изменениях реактивности, переходные процессы определяются в основном действием запаздывающих нейтронов, а при больших скачках – мгновенными нейтронами.

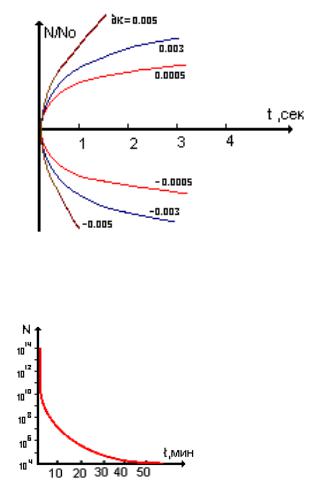
величина leff влияет только на передний фронт

нарастания

мощности;

после

этого роста,

обусловленного

мгновенными

нейтронами,

устанавливается

постоянный

период,

определяемый

 

запаздывающими нейтронами с

эквивалентным временем жизни нейтронов.

При введении отрицательной

ступенчатой

реактивности

 

после

резкого

уменьшения

мощности скорость убывания падает и дальше определяется скоростью распада ядеризлучателей запаздывающих нейтронов.

Поэтому при выключении реактора он становится доступным для проведения работ по обслуживанию примерно через 30 минут, когда плотность потока нейтронов упадет на десять порядков.

1.8 По уравнению обратных часов показать ход решения при малых и больших скачках реактивности.

 

 

 

 

 

 

 

 

6

i p

 

 

 

 

 

 

 

K leff

p

 

.

 

 

 

 

 

 

 

 

Используем уравнение обратных часов:

 

i

p i для оценки периода

 

 

 

 

 

 

 

 

 

разгона реактора при различных значениях реактивности.

 

 

 

 

 

Tp

 

1

 

 

 

 

 

 

 

 

 

p1

 

 

 

 

 

 

Заменяем:

 

 

 

 

 

 

 

 

leff

6

 

i

 

 

 

 

 

 

K

 

 

 

 

 

.

 

 

 

 

 

Tp

1 i Tp

 

 

 

 

 

 

i

 

 

 

 

 

 

В случае малых δΚ, меньших 0,5 β, значение Tp оказывается таким большим, что в знаме-

нателе 1 + λi · Tp

единицей можно пренебречь и тогда выражение примет вид:

 

l

 

6

 

i

 

1

 

 

6

 

i

 

K

eff

 

 

 

 

l

 

 

 

.

 

 

 

 

eff

 

 

 

Tp

 

i i Tp

 

 

 

 

 

 

 

 

Tp

 

i

i

6 i

Эквивалентное время жизни запаздывающих нейтронов i i на несколько порядков больше leff, поэтому для малых реактивностей:

K

1

6

 

i

 

 

 

;

 

 

 

 

Tp

i

i

то есть переходные процессы определяются в основном действием запаздывающих нейтронов.

При больших скачках реактивности, равных и больших β, период Tp мал и в знамена-теле (1) λi · Tp много меньше единицы, так что уравнение можно записать в виде:

 

leff

;

Tp

 

l

K Tp

K

 

 

 

или

 

eff

 

 

 

 

 

то есть видно, что переходные процессы будут определяться мгновенными нейтронами.

1.9 Кинетика реактора при линейном изменении реактивности в подкритическом режиме.

Кинетика при линейном изменении реактивности характеризует работу реактора при его пуске. Решение уравнений кинетики при входном сигнале вида δΚ

= At + C позволяет получить полезные сведения по проектированию системы аварийной защиты реактора для защиты от пусковых аварий. Необходимо знать, как влияет скорость изменения реактивности на рост мощности при пуске и при переходах с одного уровня мощности на другой.

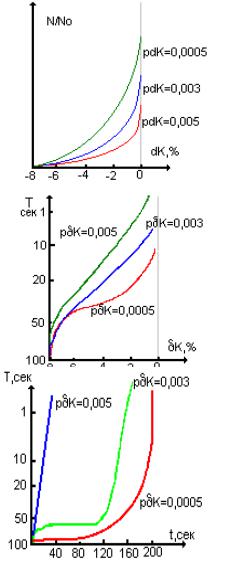
Влияние скорости линейного изменения реактивности на рост плотности нейтронов представлено на графике: →

Чем больше скорость линейного изменения δΚ, тем при меньшей плотности нейтронов достигается состояние критичности. В состоянии глубокой подкритичности все кривые сливаются, здесь рост мощности не зависит от скорости изменения реактивности. Зависимость периода от скорости линейного изменения мощности демонстрирует следующий график: →

При больших скоростях изменения реактивности период оказывается коротким и может быть измерен достаточно точно и далеко от положения критичности. Однако делать вывод о предпочтительности больших скоростей изменения реактивности еще рано. Действительно, достаточно рассмотреть графики зависимости периода от времени измерения, чтобы понять, что при больших скоростях изменения реактивности время, когда мы можем его измерять очень недолго. →

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности