
- •Заповеди для студента
- •ВАРИАНТ I
- •ВАРИАНТ II
- •ВАРИАНТ III
- •ВАРИАНТ IV
- •ВАРИАНТ V
- •ВАРИАНТ VI
- •ВАРИАНТ VII
- •ВАРИАНТ VIII
- •ВАРИАНТ IX
- •ВАРИАНТ X
- •ВАРИАНТ XI
- •ВАРИАНТ XII
- •ВАРИАНТ XIII
- •ВАРИАНТ XIV
- •ВАРИАНТ XV
- •ВАРИАНТ XVI
- •ВАРИАНТ XVII
- •ВАРИАНТ XVIII
- •ВАРИАНТ XIX
- •ВАРИАНТ XX
- •ВАРИАНТ XXI
- •ВАРИАНТ XXII
- •ВАРИАНТ XXIII
- •ВАРИАНТ XXIV
- •ВАРИАНТ XXV
- •ВАРИАНТ XXVI
- •ВАРИАНТ XXVII
- •ВАРИАНТ XXVIII
- •ВАРИАНТ XXIX
- •ВАРИАНТ XXX

ВАРИАНТ XXIX
1.Доказать, пользуясь определением предела последовательности, что
lim 1 = 0,
x→∞ n!
2.Найти предел последовательности, общий член которой
xn = n a + n3b + n
a + n3b + n c n .
c n .
3.Найти предел область определения функции:
y= arcsin(tgx).
4.Найти пределы:
1)lim |
|
1 |
|
x sin |
x |
; |
|
x→0 |
|
|
2)lim |
eαx − eβx |
; |
|
||
x→0 sinαx −sin βx |
|
|
3) xlim→∞ x2x−2 1 x4 .
5.Найти производные следующих функций:
1)y = − 2sin1 2 x + ln tgx;
2)y = − 2 +9x2 
 1+ x2 + 13 x3 arccos x.
1+ x2 + 13 x3 arccos x.
6.Исследовать функцию и построить её график:
y= 12 ln11+− xx .
7.На отрезке длиной, соединяющем два источника света силой, найти наименее освещённую точку (освещённость обратно пропорциональна квадрату расстояния от источника света).
8.Почему не верен следующий вывод теоремы Коши (функции f(x) и g(x) удовлетворяют всем условиям теоремы):
f(b)− f (a)= (b − a)f '(ξ );
g(b)− g(a)= (b − a)g'(ξ );
поделив одно равенство на другое, получим:
|
f (b) − f (a) |
= |
f '(ξ) |
. |
|
g(b) − g(a) |
|
||
|
|
g'(ξ) |
||
Где ошибка в выводе? |
|
|
|
|

ВАРИАНТ XXX
1.Доказать, что если последовательность xn сходится и все её члены положительны, то предел этой последовательности положителен или равен нулю.
2.Построить пример расходящейся последовательности, имеющей только одну предельную точку.
3.Найти область определения функции:
y= 
 sin x + cos x −1 .
sin x + cos x −1 .
4.Найти следующие пределы:
lim |
ln2 (1+ x) −sin2 x |
||||||||||||||
|
|
|
|
1− e |
−x |
2 |
|
; |
|||||||
1) x→0 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
||||
2)lim |
|
|
|
− ctg |
|
x ; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
x→0 |
x2 |
|
|
|
|
|
|
|
|
|
|
||||
5. Найти производные следующих функций: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) y = |
3 |
1 |
+ x3 |
; |
|
|
|
|
|
|
|
|
|||
1 |
− x3 |
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
a2 |
|
x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
2) y = |
x |
|
a2 − x2 + |
|
|
||||||||||
|
|
|
|
arcsin |
|
, a>0. |
|||||||||
2 |
|
2 |
a |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. Исследовать функцию и построить её график:
y = |
sin x |
|
|
; |
|
|
π |
|
|
|
sin x + |
4 |
|
|
|
|
|
|
7. Площадь листа книги равна s кв.см. Ширина полей слева и справа равна а см, а ширина полей сверху и снизу равна в см. при каких размерах листа книги площадь, занятая печатным текстом, будет наибольшей?
8. Производная f’(x) функции f(x) равна нулю при всех х из некоторого интервала (а,в).
Доказать, что f(x)=C (C-число) при всех х из этого интервала
(а,в).
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра математического моделирования
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ И ТЕОРИИ МНОЖЕСТВ
по дисциплине “Математический анализ” Методические указания для студентов первого курса Физического факультета ТюмГУ
Тюмень, 2005
Математическая логика и теория множеств – разделы математики, являющиеся одновременно фундаментом, строительным материалом, вспомогательными средствами и технологией математических построений для других разделов математики. Эта их универсальность ставит в начало изучения математических дисциплин, но на физическом факультете математическая логика и теория множеств не читаются отдельными курсами. В большинстве случаев во многих учебных заведениях эти разделы включают в математический анализ, с чего обычно и начинается вся учебная литература для естественных специальностей (по крайней мере, с множества вещественных чисел, а элементы математической логики применяются на всём протяжении как само разумеющееся).
Учитывая выше приведённые обстоятельства, а также то, что сведения в различных учебниках по математическому анализу даны не в полном объёме и существуют проблемы с обеспечением всех студентов соответствующей литературой, приходится в данные методические указания включать основные понятия и определения из математической логики и теории множеств, широко используемые в различных разделах математики.
Тема 1. Элементы логики высказываний.
§1. Высказывания и операции над ними.
Под высказыванием понимается повествовательное предложение, о котором точно известно истинно оно или нет.
Примеры высказываний:
1.Число 100 делится на 4. 2. Число 100 делится без остатка на 3.
3.Луна – спутник Земли. 4. Париж – столица Японии. 5. Черти все полосатые.
Высказывания 1.; 3. – истинные, а 2.;4. – ложные, 5. – не является высказыванием.
Высказывания принято обозначать буквами: А, B, C, D, … a, b, c, d, …, x, y, z, … . Значения, которые принимают высказывания, обозначаются буквами: И – истинно, Л – ложно.
3
Простое повествовательное предложение, принимающее истинное или ложное значение называют простым высказыванием.
Из простых высказываний можно составить сложные высказывания (как сложные предложения с помощью союзов “и”, ”или”, ”не”, ”если …, то”, ”тогда и только тогда, когда …”). При построении из простых высказываний более сложных высказываний имеем дело с операциями над высказываниями.
Отрицание.
Определение 1. Отрицанием высказывания a называется новое высказывание, обозначаемое a либо 7a и являющееся противоположным по смыслу высказыванию a. При письме отрицание образуется при помощи частицы” не”, а символ a читается “не а”.
Операция отрицания является унарной операцией (операция над одним высказыванием). Отрицание a принимает два значения И либо Л.
Пример: Пусть высказывание а: “Москва – столица России”, принимает значение И, тогда высказывание a: “Москва – не является столицей России”, принимает значение Л.
Таким образом, значения принимаемые высказыванием и его отрицанием можно представить в виде таблицы:
А |
А |
И |
Л |
|
|
Л |
И |
|
|
|
|
Дизъюнкция двух высказываний
Определение 2. Пусть а и b высказывания, тогда сложное высказывание с, обозначаемое с = a V b, называется дизъюнкцией двух высказываний а и b.
4
При написании сложного предложения простые предложения (высказывания) соединяются союзом “или”, “либо”.
Пример: Высказывание Р = (100 делится либо на 2, либо на 3) – есть дизъюнкция двух высказываний: а = (100 делится на 2), b = (100 делится на 3 (имеется в виду без остатка)), одно из которых истинно, другое ложно. Р = ( а V b) = И (истинно).
Дизъюнкция двух высказываний - бинарная операция (операция над двумя высказываниями), как и ниже рассматриваемые операции. Приведём таблицу значений для дизъюнкции высказываний а и b:
a |
b |
а V b |
|
|
|
И |
И |
И |
|
|
|
И |
Л |
И |
|
|
|
Л |
И |
И |
|
|
|
Л |
Л |
Л |
|
||
|
|
|
Как видно из таблицы значений, дизъюнкция двух высказываний истинна, если хотя бы одно высказывание истинно.
Конъюнкция двух высказываний
Определение 3. Пусть а и b высказывания, тогда сложное высказывание с, обозначаемое с = a Λ b, называется конъюнкцией двух высказываний а и b.
При письме простые предложения (высказывания) соединяются союзом “и”.
Пример: Высказывание Р = (100 делится на 2 и на 4 без остатка) – есть конъюнкция двух высказываний: а = (100 делится на 2 без остатка)
5
и b = (100 делится на 4 без остатка). Таблица значений конъюнкции двух высказываний имеет вид:
a |
b |
a Λ b |
|
|
|
И |
И |
И |
|
|
|
И |
Л |
Л |
|
|
|
Л |
И |
Л |
|
|
|
Л |
Л |
Л |
|
||
|
|
|
Отметим, что конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны.
Импликация двух высказываний
Определение 4. Пусть а и b – высказывания, тогда с = а b – сложное высказывание, которое называется импликацией двух высказываний а и b. При этом а называется посылкой, а b – заключением. При письме импликация соответствует союзу “если … , то …”.
Примеры:
1). Р = (если 100 делится на 4 без остатка, то оно делится и на 2 без остатка) – есть импликация двух высказываний:
а = (100 делится на 4 без остатка) и b = (100 делится на 2 без остатка). Оба высказывания истинны. Импликация Р = (а b) – также истинна.
2). Р = (если у льва есть когти, то снег белый) – есть импликация двух высказываний: а = (у льва есть когти) и b = (снег белый). Оба высказывания истинны и импликация Р = а b – истинна [ 1 ].
6
Легко заметить, что в отличие от двух предыдущих бинарных операций импликация не является коммутативной операцией, т.е.
а b ≠ b a.
Таблица значений импликации:
a |
b |
а b |
|
|
|
И |
И |
И |
|
|
|
И |
Л |
Л |
|
|
|
Л |
И |
И |
|
|
|
Л |
Л |
И |
|
||
|
|
|
Импликация принимает значение ложь только в том случае, когда из истинной посылки следует ложное заключение (неверный вывод). Представляется интересным, что при ложной посылке, но истинном заключении импликация истинна.
Пример. Р = (если 2 2=5, то 3 3=9) = И, хотя посылка 2 2=5 ложна, но заключение то 3 3=9 истинно.
Эквиваленция двух высказываний
Определение 5. Пусть а и b – высказывания, тогда с = а b – сложное высказывание, которое называется эквиваленцией двух высказываний а и b. Логическая операция при этом называется эквивалентностью высказываний.
При письме эквиваленция соответствует союзу “тогда и только тогда, когда … ”.
Пример. Р = [(х2 + у2 = 0) (х = 0 ) Λ (у = 0)] – эквиваленция двух высказываний: а = (х2 + у2 = 0) и b = (х = 0 ) Λ (у = 0).
7
При письме это выглядит так х2 + у2 = 0 тогда и только тогда, когда х = 0 и у = 0 одновременно.
Таблица значений эквиваленции:
a |
b |
а b |
|
|
|
И |
И |
И |
|
|
|
И |
Л |
Л |
|
|
|
Л |
И |
Л |
|
|
|
Л |
Л |
И |
|
||
|
|
|
Эквиваленция истинна тогда, когда оба высказывания истинны или оба ложны.
Пользуясь введёнными логическими операциями, можно из простых высказываний строить сложные высказывания. Например, пусть r = q Λ (p V u) – есть сложное высказывание ( конъюнкция высказывания q с дизъюнкцией высказываний p и u), R = (q Λ p) V (q Λ u) – сложное высказывание (дизъюнкция двух конъюнкций высказываний). Можно из них построить более сложные Q = (r R), что при любых зна-
чениях входящих высказываний p,q,u соответствует сложному высказыванию q Λ (p V u) (q Λ p) V (q Λ u) (доказать самостоятельно). Это выражение определяет свойство дистрибутивности операции конъюнкции относительно операции дизъюнкции.
Свойства введённых выше логических операций даны в [1],[2].
8
Тема 2 Элементы теории множеств § 2. Основные понятия, определения и обозначения.
Определение 1. Теория множеств – раздел математики, изучающий общие свойства множеств и операции над ними.
Из определения следует, что основными объектами изучения в этой теории являются множества [3].
Раскроем более подробно понятие множества. Каждый человек имеет интуитивное представление о множестве, которое у него складывается на практике. Часто при ответе на вопрос: “Что такое множество?”, большинство людей просто заменяют это слово синонимами: совокупность, семейство, класс, система, ансамбль, коллекция и т.д. предметов (объектов).
Безотносительно к чему – либо это понятие является неопределяемым, т.е. первичным понятием, как и многие другие понятие, например, яблоко, стол, стул, время, трава и др.
Можно понятию множества дать строгое определение, если за неопределяемое взять другое понятие или определить понятие множества через свойства входящих в него элементов (через аксиомы) [4], [5]. Поскольку понятие множества в математике применяется практически во всех её разделах, приведём некоторые его определения, встречающиеся в литературе [1], [3].
“Множество – одно из основных понятий математики: набор, каких
– либо различных объектов или элементов, рассматриваемый как одно целое; если множество задано перечислением его элементов, то такое множество обозначают в виде { a,b,c,…}, если же имеется правило для определения принадлежности элементов множеству, то множество обозначается в виде {х:…} или {х|…}, где за двоеточием или вертикальной
9
чертой указываются условия, которым должен удовлетворять элемент х, чтобы принадлежать рассматриваемому множеству; синонимы: набор, совокупность, система, комплект, класс” [3].
По-видимому, такое определение оставляет чувство неудовлетворённости, поскольку заменяется синонимами и содержит в себе обозначения множества.
Приведём цитату из книги Р.Т. Вольвачёв “Элементы математической логики и теории множеств” 1986 [1]: “Существенным в понятии “множество” является то, что, мы объединяем некоторые предметы в одно целое. Георг Кантор (1845 – 1918), немецкий математик, создатель теории множеств, так подчеркнул это обстоятельство: “Множество есть многое, мыслимое нами как единое”.
Думается, что определение Кантора более симпатично, поскольку довольно краткое и точно отражает сущность понятия.
Так как на практике построение множеств осуществляется объединением рассматриваемых объектов в одно целое по какому – либо признаку, свойству или отношению, то можно дать следующее определение понятию множества:
Определение 2. Множество – нечто целое в рассматриваемом отношении, состоящее из частей, неделимых в данном отношении (эти части называют элементами множества).
Например, все мужчины на Земле составляют некоторое множество в отношении пола, каждый мужчина есть элемент этого множества. Если же рассматривать всех людей на Земле, то в этом отношении мужчины образуют подмножество мужчин во множестве всех людей, так же, как женщины образуют подмножество женщин множества людей.
Поэтому множество можно рассматривать и как множество и как подмножество некоторого другого множества в зависимости от того, в каком отношении его рассматривать. Такое понимание множества ис-
10
ключает противоречивое понятие множество всех множеств, являющееся тавтологией.
Множества принято обозначать большими буквами, например, А, B, C, D,…, X, Y, Z, … и т.д. Элементы этих множеств обозначают маленькими буквами: a, b, c, d, …, x,y,z, … и т.д.
Для обозначения принадлежности элемента множеству применяется квантор (значок) принадлежности (включения): , например, х Х (читается: х принадлежит множеству Х) либо Х х (читается множество Х содержит или включает элемент х).
Определение 3. Множество, состоящее из конечного числа элементов, называется конечным множеством, в противном случае - бесконечным множеством.
Например, А = {a1, a2, a3, …,an}, где n – конечное число; X = {1, 2, 7, 8};
множество электроном в атоме и т.д. Множество натуральных чисел N – бесконечное множество.
Таким образом, множество может состоять из одного, двух, трёх, и т.д. элементов. Например, множество северных магнитных полюсов планеты Земля состоит из одного элемента, так как у земли один северный магнитный полюс; множество всех полюсов (включая и географические полюса), состоит из четырёх элементов; множество натуральных чисел: N = {1, 2, 3, …,n, n+1, …,∞} – бесконечное множество; Z = {-∞, …, -n, …, -2, -1, 0, 1, 2, …, n, n+1, …, …,+∞} так же бесконечное множество.
В теории множеств по необходимости вводится понятие пустого множества, обозначаемого . Это множество не имеет элементов. Например, = { x: sinх > 1, x R}; множество трёхголовых драконов в настоящее время на Земле есть пустое множество и т. д.
Определение 4. Все бесконечные множества, элементы которых можно занумеровать (т.е. каждому элементу множества присвоить но-
11

мер – число из множества натуральных чисел) называют счётными множествами.
Например, множество всех целых чисел; множество всех рациональных чисел Q = {q: q = mn , где m Z Λ n N} [6].
Бесконечные множества, все элементы которых не удаётся пронумеровать (т.е. не хватает чисел из N) называют несчётными множествами. Примером несчётного множества может служить множество всех вещественных чисел из отрезка [0,1] и др. множества [6].
Для дальнейшего нам понадобятся кванторы существования и общности аналогично рассмотренному выше квантору принадлежности. Кроме квантора принадлежности элемента х множеству Х: х Х, используют квантор включения для множеств: A B ( множество А входит или включено во множество B). Другими словами, множество А включено (содержится) в множестве B, если все элементы а множества А одновременно являются элементами множества B, т.е. все элементы множества А обладают признаком присущим элементам множества B. Приняты обозначения для отрицания принадлежности и включения:
(a A) a A a A (здесь три записи, выражающие одно и то же: элемент а не принадлежит множеству А).
Аналогично: (A B) A B A B.
Квантор существования :
х А: Ф(х) – существует элемент х принадлежащий множеству А и удовлетворяющий свойству Ф(х). Можно прочесть символьную запись и так: найдётся хотя бы одно х принадлежащее множеству А, обладающее свойством Ф(х).
Квантор общности :
х А – означает: для любого (для всех) х, принадлежащего (принадлежащих) множеству А.
12
Используя квантор включения, можно дать определения подмножества и равенства двух множеств.
Определение 5. Множество B называется подмножеством множества А, если все элементы множества B являются и элементами множества А.
Символическая запись этого определения запишется в виде:
B A a A a B.
Другими словами B – есть подмножество множества А, если
(B A) Λ (A B).
Определение 6. Два множества А и B называются равными, если
B A A B a B ( А = B А B Λ B A).
§ 3. Операции над множествами и их свойства.
Новые множества можно конструировать из имеющихся множеств с помощью операций над ними. Под операцией над множествами будем понимать правило, по которому из двух множеств строится третье множество.
Рассмотрим основные операции.
1. Объединение множеств.
Операция объединения множеств обозначается значком U. Пусть существуют не пустые множества A и B, тогда их объединением будет множество C, состоящее как из элементов множества A, так и из элементов множества B, взятых по одному разу:
x (C = A B) (x A) (x B).
Определение 1. Объединением множеств A и B называется множество, обозначаемое АUB и состоящее из всех тех элементов, которые принадлежат либо множеству А либо множеству В:
АUB = {x: x A V x B}, т.е. элементы х объединения АUB обладают качеством присущим элементам множества А либо элементам множества В.
13

Примеры:
1). Геометрический:
А |
В |
А В. |
2). Алгебраический: {1, 2, 3}U{2, 3, 4, 5} = {1, 2, 3, 4, 5}.
Замечание.
Если Аi , i = 1, 2, 3, …, n, тогда можно определить
n
A = Ai = A1 A2 A3... An .
i=1
2.Пересечение множеств.
Операция пересечения обозначается значком . Пусть существуют не пустые множества А и В, тогда пересечением этих множеств будет множество С, состоящее из элементов принадлежащих одновременно множеству А и множеству В, взятых один раз:
x (C = A B) (x A) (x B).
Определение 1. Пересечением множеств A и B называется мно-
жество, обозначаемое A B и состоящее из всех тех элементов, которые принадлежат одновременно множествам А и В: A B = {x: x A Λ x B}, т.е. элементы х пересечения A B обладают качеством присущем одновременно элементам множества А и элементам множества В.
Примеры:
1). Геометрический:
А |
|
|
В |
|
|
А∩В. |
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2). Алгебраический: |
{1, 2, 3}∩{2, 3, 4, 5} = { 2, 3}. |
|
||||
Замечание. |
|
|
|
|
||
14
Если Аi , i = 1, 2, 3, …, n, тогда можно определить
n
A = Ai = A1 A2 A3... An .
i=1
3.Свойства операций объединения и пересечения множеств.
1). Операции объединения и пересечения множеств коммутативны:
A B = B A; A B = B A.
Определение 3. Любая операция T над множествами А и В называется коммутативной операцией, если она удовлетворяет условию ATB = BTA.
Доказательство коммутативности операций объединения и пересечения множеств очевидно, например, для объединения:
(x A B) (x A) (x B) (x B) (x A) (x B A), в силу
коммутативности логической операции – дизъюнкции.
2). Операции объединения и пересечения множеств ассоциативны:
A (B С) = (A B) C; A (B C) = (A B) C.
Доказательство для объединения:
x (A (B C)) ((x A) (x (B C))) (x A) (x B) (x C)
((x A) (x B)) (x C) (x (A B)) (x C) x ((A B) C),
аналогично доказывается в обратную сторону. Ч.Т.Д.
То же самое доказательство можно провести для пересечения (самостоятельно).
Определение 4. Любая операция T над множествами А, В и С называется ассоциативной, если удовлетворяет следующему условию АТ(ВТС) = (АТВ)ТС.
3). Операция объединения множеств дистрибутивна относительно операции пересечения множеств: А (В С) = (А В) (А С).
Доказательство
15
x (A (B C)) (x A) (x (B C)) (x A) [(x B) (x C)]
[(x A) (x B)] [(x A) (x C)] [(x (A B)] [x (A C)]
x [(A B) (A C)].
При доказательстве использовалась дистрибутивность дизъюнкции относительно конъюнкции, аналогично доказательство в обратную сторону. Ч.Т.Д. 4). Операция пересечения множеств дистрибутивна относительно операции объединения множеств: А (В С) = (А В) (А С). Доказательство аналогично пункту 3).(доказать самостоятельно).
Определение 5. Любая операция T называется дистрибутивной относительно операции , если удовлетворяет условию АТ(В С) = (АТВ) (АТС), для А, В.С.
5). Унарные операции над множеством: A A = A; |
A A = A. |
Доказательство по определению (самостоятельно). |
|
4. Разность множеств. Дополнение.
Операция разности множеств обозначается значком “ \”. Пусть существуют не пустые множества A и B, тогда их разностью будет множество C, состоящее только из элементов множества A, не принадлежащих множеству B:
x (C = A \ B) (x A) (x B), т.е. элемент х разности А \ В, обладает признаком элементов множества А и не обладает признаком элементов множества В.
Определение 6. Разность двух множеств А и В называется множество, обозначаемое А \ В и состоящее только из тех элементов, которые принадлежат множеству А, но не принадлежат множеству В:
А\ В ={x : (x A) (x B)}.
16
Определение 7. Пусть множество А – подмножество множества Е. Дополнением множества А до множества Е называется множество Е \ А, обозначаемое СЕ А и состоящее из всех тех элементов множества Е, которые не принадлежат множеству А.
Если ясно, о каком множестве Е идёт речь, то вместо СЕ А пишут СА либо А(не надо путать с отрицанием). Поскольку последнее обозначение дополнения более удобно при записи, будем его употреблять:
А={x : (x E) (x A E)}.
Примеры разности множеств:
1). Геометрический:
А |
В |
А\ В |
2). Алгебраический: {1, 2, 3} \ {2, 3, 4, 5} = {1}.
Примеры дополнения множества:
1). Геометрический:
А |
|
Е |
Е \ А |
2). Алгебраический: А = {4,5}; |
E = {1, 2, 3, 4, 5}, тогда |
СЕ А= Е \ А = А = {1, 2, 3}. |
|
5. Симметрическая разность множеств.
Пусть А и В – не пустые множества, тогда их симметрической разностью называется множество, обозначаемое А ∆ В, состоящее из тех элементов, которые принадлежат А В, но не содержат элементов из множества А В.
17
Определение 8. Симметрической разностью множеств А и В называется множество, обозначаемое А ∆ В и состоящее из тех элементов, которые принадлежат либо А \ В либо В \ А :
А∆В = (А\ В) (В\ А) (А В) \ (А В).
Примеры симметрической разности множеств:
1). Геометрический:
2). Алгебраический: {1, 2, 3} ∆ {2, 3, 4, 5} = {1, 4, 5}.
Свойства симметрической разности множеств определить самостоятельно,
например, А ∆ А = ; если А Е, то А ∆ Е = А.
6. Прямое произведение множеств.
Пусть А и В – не пустые множества, тогда их декартовым или прямым произведением называется множество, обозначаемым А × В, состоящее из пар (а, b) таких, что (а А)Λ(b В):
A×B ={(a,b) : (a A) (b B)}.
Так же множество С = А × В называют прямым, Декартовым произведением двух множеств А и В.
Определение 9. Декартовым (или прямым) произведением множеств А и В называется множество С, обозначаемое А × В и содержащее все пары (а,b), таких, что (а А) Λ (b B).
Пример. Пусть А = {1, 2, 3, 4, 5} и B = {0, 1}, тогда А × В = {(1,0); (1,1); (2,0); (2,1); (3,0); (3,1); (4,0); (4,1); (5,0); (5,1)}.
B × A = {(0,1); (0,2); (0,3); (0,4); (0,5); (1,1); (1,2); (1,3); (1,4); (1,5)}.
Откуда видно, что операция произведения двух множеств не коммутативна. А × А – декартово произведение множества А на само себя. Геометрическим образом декартова произведения R2 = R × R, является
18
множество точек на плоскости (двухмерное пространство). Геометрическим образом декартова произведения множества R трижды на себя: R3 = R × R × R – множество точек трёхмерного пространства. Аналогично можно построить n – мерное пространство: Rn = R × R × … × R (произведение множества R само на себя n раз). Для произведения различных множеств приняты следующие обозначения:
Пусть Аi i = 1, 2, 3,…, n,…; Аi ≠ для любого i, тогда
n |
n |
|
|
A = ∏Ai = Ai = A1 |
× A2 |
×...× An . Элементом множества А является |
|
i=1 |
i=1 |
|
|
a = (a1, a2, …,an), где аi Ai, i = 1, 2, 3,…,n. В этом наборе на i – том ме-
сте стоит элемент из множества Аi [1].
Определение 10. Множество D ={(a,b) : a A b B a = b
называется диагональю множества А × В.
Например, D = {(1,1); (2,2); (3,3);…; (10,10)} является диагональю множе-
ства E2, где Е = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
§ 4. Отображение множеств.
Пусть Х и У не пустые множества.
Определение 1. Отображением F множества Х на множество У называется правило или закон, по которому каждому элементу х множества Х ставится в соответствие элемент у множества У.
При этом множество Х называется областью определения (задания) отображения F, а множество У называется множеством значений отображения F.
Для отображений приняты следующие обозначения:
F : X →Y x y y = F(x).
19
Первое обозначения применяется когда хотят сказать, что множество Х отображается на множество У. Второе обозначение применяется, когда хотят сказать, что каждому элементу х множества Х ставится в соответствие по закону F элемент у множества У. Третье обозначение, чаще всего употребляется, так как оно является аналитическим заданием отображения F и даёт конкретное правило, по которому каждому значению х ставится в соответствие значение у.
В литературе очень часто встречаются синонимы отображения, которые исторически возникли при изучении отображений. Так например, если Х и У – числовые множества, то отображение F называют числовой функцией одной переменной (величины) или одного переменного (аргумента). Исходя из этого, можно дать полное определение числовой функции одной переменной.
Определение 2. Функцией f числового аргумента х Х называется правило или закон, по которому каждому элементу х Х ставится в соответствие число у У: f = X →Y y = f (x).
Примером числовой функции может служить любая элементарная функция, изучающаяся в школе, например,
y = x2 , где x R, y R |
{0}, |
где R+ - множество положитель- |
+ |
|
ных, вещественных чисел.
Символическую запись можно расшифровать так: функция f есть правило (необходимо число х на само себя), по которому каждому числу из множества действительных чисел ставится в соответствие число из множества положительных вещественных чисел, с нулём. Другими словами, 0 ставится в соответствие 0, числу 0,5 ставится число 0,25, числу 1 ставится число 1, числу (-1) ставится в соответствие 1 и т.д.
20

Если множество Х – произвольное множество, а У является числовым множеством, тогда отображение F: X→Y часто называют функционалом (дать полное определение функционала).
Пример. Пусть f F (F – множество интегрируемых функций на отрезке
[a,b]), тогда определённый интеграл I = ∫b f (x)dx - есть функционал на
a
множестве F. I = F → R, при заданных а и b, так как каждой функции f,
I сопоставляет число из R, например, I = ∫1 хdx = 0,5, функции у = х ставит-
0
ся в соответствие число 0,5. Само правило, по которому функции ставится в соответствие число, даётся формулой Ньютона – Лейбница:
∫b f (x)dx = F(b) − F(a).
a
Если Х и У являются произвольными множествами (например, множествами функций), тогда F = X → Y называют оператором. Заметим, что определение оператора мало чем отличается от отображения. Таким образом, в рассматриваемом частном случае оператор каждой функции f Х ставит в соответствие функцию ϕ(х) : ϕ У.
Пример. Пусть Х – множество дифференцируемых функций на от-
резке [a,b], тогда df (x) =ϕ(x) Y , т.е. оператор дифференцирования на dx
Х, каждой функции из Х ставит функцию ϕ У по следующему правилу:
lim |
f (x + ∆x) − f (x) |
=ϕ(x), |
x [a,b]. |
|
∆x |
||||
∆x→0 |
|
|
Например, dxd (x) =1, оператор дифференцирования ставит в соответ-
ствие функции f(x) = x постоянную функцию ϕ(х) =1. для любого х R;
d |
(x2 ) = 2х х2 2х; |
d |
|
|
|
1 |
|
|
|
|
1 |
|
|
||
(3 |
x) = |
|
3 x |
и т.д. |
|||||||||||
dx |
dx |
|
|
|
33 |
|
|
||||||||
33 x2 |
x2 |
||||||||||||||
21
Если элементами множества Х являются множества Аi, а У числовое множество, то F = X → Y отображение называется мерой (самостоятельно дать полное определение меры).
Пример. Пусть Х множество прямоугольников на плоскости со сторонами длины х и у, тогда каждому прямоугольнику множества Х можно сопоставить число х у, характеризующее площадь прямоугольника (количество места занимаемого на плоскости), т.е. мерой площади прямоугольника является функция двух переменных S = f(x,y) = х у. Так прямоугольнику со сторонами длины 1ед. и 2ед. ставится в соответствие число 2 ед2.
Таким образом, мерой площади прямоугольников со сторонами х и у является правило f : X → R0+ , где R0+ = R+ {0}, по которому каждому
множеству точек на плоскости, заключённых в прямоугольнике сопоставляется число, являющееся площадью прямоугольника.
Пусть X, Y, Z – не пустые числовые множества и задано отобра-
жение F: X × Y → Z (x, y) z z = F(x,y), т.е. отображение декартового произведения множеств Х и У на множество Z. В этом случае F называют функцией двух переменных (величин или аргументов х и у).
Если X R, Y R, Z R, то геометрическим образом декартова произведения X × Y, является вся плоскость либо её часть, следовательно, областью определения функции двух переменных является вся плоскость либо её часть. Другими словами, функция двух переменных отображает плоскость либо её часть на множество вещественных чисел (вещественную ось) либо его часть.
Пример. z = x2 + y2 , по значениям х и у находятся по указанному правилу число z, при этом х и у называются независимыми переменными или аргументами, а z – зависимой переменной или значением функции двух переменных.
22
Аналогично можно построить отображения трёх, четырёх и т.д. переменных. Таким образом, отображение F: X → Y , будет называться функцией нескольких переменных ( n переменных), если
|
n |
|
|
|
|
|
|
|
|
X = ∏Xi и обозначается в виде y = f (x1, x2 ,..., xn ) x y, |
|||||||||
|
i=1 |
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
x = (x1, x2,..., xn ) : |
xi X i , |
i =1,2,3,...,n. |
|
|
|||||
Примеры: |
|
|
|
|
|
|
|
||
|
y = |
n |
|
n |
|
|
|
n |
|
1). |
∑xi2 ; |
2). |
y = ∏(xi − xi−1 ); |
3). |
y = sin |
∑αi . |
|||
|
= |
= |
|
|
i=1 |
|
|||
|
|
i 1 |
|
i 1 |
|
|
|
||
Функция нескольких переменных (n переменных) отображает n – мерное пространство (либо его часть) на вещественную прямую (либо её часть).
Определение 3. Отображение F называется тождественным, если
F: X → Y x x x = F(x).
Другими словами тождественное отображение элементу х из множества Х ставит в соответствие тот же самый элемент х. Например, у = х, есть тождественное отображение R → R, так как для любого значения х даёт тоже значение, например, х = 1 и у = 1; х = -2 и у = -2; х = 0,25 и у = 0,25 и т. д.
Определение 4. Пусть X, Y, Z – не пустые числовые множества и заданы отображения f: X → Y Λ g: Y → Z, тогда отображение F: X → Z, обозначаемое F(x) = (g ° f)(x) = g(f(x)) = z называется композицией отображений f и g (или сложной функцией от х, приняты так же названия: суперпозиция двух функций и функция от функции).
23

Символически композиция отображений f и g записывается в виде:
F = g ° f.
Пусть Xi, i = 1, 2, 3,…,n и fi: Xi → Xi+1, тогда
f: X1 → Xn+1 f (x) = ( fn fn−1 fn−2 ... f2 f1 )(x) называется композицией n функций.
Пример. y = cos(x); z = ln|y|; g = z-1, тогда композицией трёх функций (или сложной функцией) будет:
u = ln cos1 x u = 1z = ln1y = ln cos1 x .
Определение 5. Отображение F: X → Y называется сюръекцией (или сюръективным), если ля любого у Y найдётся, хотя бы один, элемент х Х.
Для сюръективного отображения у каждого элемента множества Y имеется прообраз из множества Х, говорят, что это отображение на множество Y, в отличие от отображения во множество Y.
Определение 6. Отображение F: X → Y называется инъекцией (или инъективным), если для любых х1 и х2 из множества Х таких, что из х1 ≠ х2 следует, что F(x1) ≠ F(х2).
Инъективное отображение это такое отображение, при котором любым двум различным значениям из множества Х соответствуют два различных значения (образы) отображения во множество Y .
Определение 7. Отображение F: X → Y называется биекцией (или взаимно однозначным отображением), если оно одновременно сюръективно и инъективно.
Символически это определение можно записать так F: X → Y – биекция,
если y Y x X Λ х1 ≠ х2 y1 ≠ y2 .
Примеры инъекций, сюръекций и биекций можно найти в [1].
24

Определение 8. Пусть существуют отображения F: X → Y и
Ф: Y → X. Отображение Ф называется обратным к отображению F, если композиция (Ф ° F)(x) = IX – есть тождественное отображение множества Х на себя. Также F называется обратным к отображению Ф, если композиция (F ° Ф)(у) = IY – есть тождественное отображение множества Y на себя.
Когда отображение Ф есть обратное к F и одновременно F есть обратное отображение к Ф, то в этом случае говорят о взаимообратном отображении и обозначают Ф = F-1.
На практике, если задана функция y = f(x), обратную к ней функцию определяют, решая уравнение относительно аргумента х как функции значения y: y = f(x) x = f-1(y). Другими словами, если функция задана аналитически, то используя известные алгебраические операции переменную х выражают через переменную у.
Примеры:
1). Пусть y = 1x = f (x) : R \{0} → R \{0}, тогда обратная к ней будет
функция:
x = 1y = f −1 (y) : R \{0} → R \{0}.
2). Пусть y = 11+− xx = f (x) : R \{−1} → R \{−1}, тогда обратная к ней функция
будет x = 11+− yy = f −1 (y) : R \ {−1} → R \ {−1}.
Легко проверить, что это взаимообратные функции. Критерий, позволяющий судить о существовании обратного отображения, даёт следующая теорема [1].
Теорема. Отображение F: X → Y тогда и только тогда обратимо, когда оно биективно.
25
Определение 9. Графиком отображения F: X → Y называется множество упорядоченных пар чисел таких, что одно из них принадлежит множеству Х, а другое множеству Y и оба удовлетворяют соотноше-
нию y = F(x).
Символически это определение записывается в виде:
Г ={(x, y) : x X y Y : y = F(x)} X × Y.
Геометрическим образом графика функции одной переменной является линия на плоскости, например,
1) у = х 2) у = х2
3) у = х3 |
4) у = sinx |
Геометрическим образом графика функции двух переменных является поверхность в трёхмерном пространстве:
Г ={(x, y, z) : x X y Y z Z : z = F(x, y)} X × Y × Z.
Например,
26

1)x2 + y2 + z2 = R2 z = ±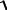
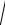 R2 − x2 − y2 , графиком этой функции является сфера:
R2 − x2 − y2 , графиком этой функции является сфера:
2)z = x2 + y2 , графиком этой функции является поверхность в трёхмерном пространстве, которая называется параболоидом вращения:
С помощью понятия отображения можно ввести понятие эквивалентности множеств и связанное с ним понятие мощности множества.
Определение 10. Множество Х эквивалентно множеству Y, если между ними можно установить взаимно однозначное соответствие (биекцию).
Говорят, что два множества равномощны (имеют одинаковую мощность), если они эквивалентны.
Для конечных множеств понятие мощности совпадает с количеством элементов этого множества. Для бесконечных множеств нельзя говорить о количестве элементов, поэтому это понятие и заменяют мощностью множеств. В связи с этим можно сказать, что мощность множества характеризует на сколько “богато” множество элементами. Для обозначе-
27
ния мощности множества вводят кардинальное число: cardR - кардинальное число множества R или мощность множества.
Все множества эквивалентные множеству натуральных чисел N имеют одно и то же кардинальное число и называются счётными множествами мощности а. Все множества эквивалентные множеству вещественных чисел так же имеют одинаковую мощность ( а следовательно, кардинальное число) и называются несчётными множествами мощности континуум с. Таким образом, для бесконечных множеств понятие мощности множества является обобщением понятия количества элементов для конечного множества.
§ 5. Бинарные отношения на множестве.
Определение 1. Пусть Е – некоторое множество, а множество А есть подмножество из множества Е × Е; говорят, что два элемента х,у Е связаны бинарным отношением, определяемом посредством множества А, если (х,у) А.
Иногда бинарное отношение обозначают каким – либо символом: хϕу, т.е. х и у находятся в бинарном отношении ϕ. В более конкретных случаях ϕ ; ϕ =; ϕ и т.д. х у; х = у: х у и т.д.
Примеры бинарных отношений:
1). Пусть Е = N – множество натуральных чисел, А Е × Е - множество пар натуральных чисел (p,q), для которых p + q – чётное число: pϕq p + q – чётное число.
2). Пусть Е – множество кругов на плоскости, тогда бинарное отношение ϕ между двумя кругами может быть установлено, скажем, так: радиус одного круга в два раза больше радиуса другого круга.
Замечание. Если задано бинарное отношение ϕ для пары элементов из Е, то ещё не означает, что отношение выполняется для любой пары.
28
Определение 2. Отношение ϕ называется рефлексивным, если хϕх справедливо для всех элементов из Е, т.е. всегда (х,х) А.
При этом говорят, что множество А содержит диагональ множества Е × Е. Если ϕ , тогда рефлексивность обозначается х х.
Определение 3. Отношение ϕ называется симметричным, если хϕу Λ уϕх, т.е. если (х,у) А, то и (у,х) А.
Например, х у у х.
Определение 4. Отношение ϕ называется транзитивным, если хϕу Λ уϕz хϕz, т.е. если (х,у) А Λ (y,z) А , то и (x,z) А. Например, х у z х z.
Определение 5. Отношение ϕ называется антисимметричным, если хϕу Λ уϕх х = у.
Определение 6. Отношение ϕ на множестве Е называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно:
1.хϕх, для х Е.
2.хϕу Λ уϕх, для любых пар (х,у) Е.
3.хϕу Λ уϕz хϕz, х,у,z Е.
Пример. Между двумя парами натуральных чисел (p,q) и (p’ , q’) уста-
навливается отношение ϕ: ( p,q)ϕ( p′,q′) p q′ = p′ q или отношение
r: ( p,q)ϕ( p′,q′) p + q′ = p′+ q. Легко проверить все условия определе-
ния и показать, что это есть отношения эквивалентности; первое служит для определения рациональных чисел, а второе – дя определения целых положительных чисел, здесь E = N × N.
Отношение эквивалентности, заданное на каком – либо множестве, позволяет разбить его на непересекающиеся классы элементов эквивалентных друг другу.
29
Каждый класс однозначно определяется любым своим элементом, так как, два элемента эквивалентные третьему, эквивалентны между собой (условие транзитивности). Условие рефлективности обеспечивает принадлежность любого элемента, какому – либо классу (например, классу, определяемому самим этим элементом).
Пример. На множестве натуральных чисел N введём отношение эквивалентности следующим образом: два числа p и q эквивалентны, если их модуль разности делится на 3 (без остатка). Легко убедиться, что это отношение эквивалентности (самостоятельно).
Возьмём число 1, тогда |1-1| делится на 3, поскольку 0 длится на любое число кроме себя. Таким образом, поместим 1 в класс I, и будем считать 1 представителем класса I. Далее возьмём число 2, поскольку |2-1| не делится на 3, то его в этот класс не вносим, тогда берём число 3, но |3-1|, так же не делится на 3, возьмём число 4, при этом |4 -1| = 3, то число 4 эквивалентно 1 и его помещаем в тот же класс I. Продолжая выбор чисел, убедимся, что в этот класс могут быть занесены все числа m = 3k + 1, таких что |m -1| = 3k (k = 0, 1, 2, …, …). Теперь из оставшихся чисел по элементу 2 также образуем класс II, в который войдут все чис-
ла m = 3k + 2 таких, что |m -2| = 3k (k = 0, 1, 2, …, …). Из оставшихся чи-
сел по элементу 3 образуется класс III, состоящий из элементов
m = 3k + 3 таких, что |m - 3| = 3k (k = 0, 1, 2, …, …). После чего все эле-
менты будут определены в три класса: I,II,III:
Класс I = {1, 4, 7, 10, 13, 16,…, 3k+1,…}. Класс II = {2, 5, 8, 11, 14, 17,…, 3k+2,…}. Класс III = {3, 6, 9, 12, 15, 18,…, 3k+3,…}.
Определение 7. Отношение ϕ на множестве Е называется отношением порядка, если оно рефлексивно, антисимметрично и транзитивно:
1.хϕх, для х Е.
2.хϕу Λ уϕх х = у, для любых пар (х,у) Е.
30
3. хϕу Λ уϕz хϕz, х,у,z Е.
Например, хϕу х ≤ у – есть отношение порядка. Легко проверить все свойства отношения порядка по определению:
1. х ≤ х.
2. х ≤ у Λ у ≤ х х = у.
3. х ≤ у Λ у ≤ z х ≤ z.
Определение 8. Множество, на котором задано отношение порядка, называется частично упорядоченным множеством.
Определение 9. Если для любых х,у Е определено х ≤ у V у ≤ х , то множество Е называется линейно упорядоченным множеством. Например, множество вещественных чисел есть линейно упорядоченное множество (показать по определению самостоятельно). Отношение порядка позволяет сравнивать элементы множества и приводит к таким понятиям как наибольший и наименьший элементы множества.
Определение 10. Пусть дано Е, элемент а Е называется наименьшим элементом множества Е, если х Е выполняется а ≤ х. Определение 11. Пусть дано Е, элемент b Е называется наибольшим элементом множества Е, если х Е выполняется х ≤ b.
Примеры:
1). Е = {1, 2, 3, …, 10}, в этом множестве существует наименьший элемент 1, и наибольший элемент 10.
2). Е = (0,1], в этом множестве нет наименьшего элемента, но есть наибольший элемент 1.
3). Е = [0,1), в этом множестве нет наибольшего элемента, но есть наименьший элемент 0.
31
4). Е = (0,1), в этом множестве отсутствуют наибольший и наименьший элементы.
Определение 12. Пусть А Е. Элемент с Е называется верхней гранью множества А (нижней гранью), если для х А, выполняется
c ≥ x (c ≤ x) .
У множества может быть бесконечно много верхних и нижних граней. Примеры:
1). А = [0,1] R. У множества А имеется бесконечно много как нижних, так и верхних граней.
2). Множество отрицательных вещественных чисел R- R. У этого множества бесконечно много верхних граней и нет ни одной нижней грани. 3). Множество положительных вещественных чисел R+ R. У этого множества бесконечно много нижних граней и нет ни одной верхней грани.
4). Множество всех действительных чисел R, у этого множества нет ни верхних, ни нижних граней – множество вещественных чисел неограниченное множество.
Определение 13. Множество, имеющее хотя бы одну верхнюю (нижнюю) грань, называется ограниченным сверху (снизу).
Определение 14. Множество, ограниченное сверху и снизу называется ограниченным множеством.
В качестве примеров можно взять выше приведённые примеры. Определение 15. Наименьшая верхняя грань множества А назы-
вается точной верхней гранью множества А и обозначается supA (читается супремум множества А).
Пример. Пусть А = [0;1], тогда supA = 1.
32
Определение 16. Наибольшая верхняя грань множества А называется точной нижней гранью множества А и обозначается infA (читается инфинум множества А).
Пример. Пусть А = [0;1], тогда infA = 0.
Теорема. Всякое не пустое множество, ограниченное сверху (снизу) имеет точную верхнюю грань (точную нижнюю грань). Доказательство см. в [7],[8].
В заключение параграфа отметим, что бинарные отношения на множестве могут быть заданы с помощью отображений.
Пусть дано f: E → F, определим бинарное отношение ϕ в Е следую-
щим образом: хϕу f(x) = f(y), x,y E, f(x),f(y) F.
Проверим, что это есть отношение эквивалентности:
1.Рефлексивность: хϕх f(x) = f(х).
2.Симметричность: хϕу уϕх f(x) = f(у) f(у) = f(х).
3.Транзитивность:
xϕy yϕz xϕz f (x) = f (y) f (y) = f (z) f (x) = f (z).
При доказательстве используются элементарные свойства функции.
33
ЛИ Т Е Р А Т У Р А
1.Вольвачёв Р.Т. Элементы математической логики и теории множеств.
Минск. 1986.
2.Никольская И.Л. Математическая логика. М.: 1981. 127 с.
3.Каазик Ю.Я. Математический словарь. Таллин. “ ВАЛГУС” 1985. 296 c.
4.Кириллов А.А., Гвишиани А.Д. Теоремы и задачи функционального анализа. М.: “Наука”. 1979. 384 с.
5.Акилов Т.П. Дятлов В.Н. Основы математического анализа. Новоси-
бирск. 1980.
6.Колмогоров А.Н. Фомин С.В. Элементы теории функций и функционального анализа. М.: “Наука”. 1976. 544 с.
7.Кудрявцев Л.Д. Курс математического анализа. В 3-х т. Том 1. М.:
“Высшая школа” 1988. 712 c.
8.Шипачёв В.С. Высшая математика. М.:Высшая школа. 1996. 479 с.
9.Дёгтев А.Н. Алгебра и логика. Тюмень: “Тюм.Г.У.” 2000. 88 c.
34
(Сборник задач по курсу математического анализа. Г.Н.Берман)
№ 269
Вычислить предел функции в точке х = 0:
|
|
3 |
−3x +1 |
|
||
|
|
x |
|
|
||
|
|
|
|
|
||
lim |
|
x − 4 |
+1 . |
|||
x→0 |
|
|
|
|||
РЕШЕНИЕ
Так как знаменатель дроби при x = 0 не равен нулю, то находим предел в точке x = 0, подстановкой значения аргумента:
|
|
|
|
|
|
|
x |
3 |
−3x +1 |
|
|
1 |
|
3 |
|
|||
|
|
|
|
|
|
|
|
|
= − |
+1 = |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
lim |
|
|
x − 4 |
+1 |
4 |
4 |
||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|||||||
|
|
3 |
− 3x +1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
|
|
x |
|
|
|
= |
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: lim |
|
x − 4 |
+1 |
4 |
|
|
|
|
|
|
|
|||||||
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
№277 Вычислить предел функции в точке х = 0:
|
|
1 |
|
3 |
|
|
lim |
|
− |
|
|
. |
|
1− x |
1− x |
3 |
||||
x→1 |
|
|
|
|
||
РЕШЕНИЕ
Так как знаменатель дроби стремится к нулю при x → 0, то имеем неопределённость типа: ∞ - ∞. Для нахождения предела преобразуем данную дробь.
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1+ x + x2 −3 |
|
|
|
(x −1)(x + 2) |
|
|
|
|
− (x + 2) |
|
|||
lim |
|
|
|
− |
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
= lim |
|
|
|
= lim |
|
|
|
|
= −1. |
||||
|
|
− x |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
x→1 |
1 |
|
1 |
− x |
|
|
|
|
|
x→1 |
|
(1 |
− x)(1+ x + x |
|
) |
x→1 |
(1− x)(1+ x + x |
|
) |
x→1 |
1 |
+ x + x |
|
|
|||||||
Ответ: lim |
|
1 |
|
− |
|
|
3 |
|
|
|
= −1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1− x |
1 |
− x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
№ 282 Вычислить предел функции в точке х = ∞:
lim |
|
x4 −5x |
|
|
x |
2 |
−3x +1 . |
||
x→∞ |
|
|||
РЕШЕНИЕ
Функция при x→ ∞ является бесконечно большой последовательность. Для нахождения предела надо числитель и знаменатель поделить на x с большей степенью.
|
|
|
1− |
|
5 |
|
|
|
|
||
lim |
|
|
x3 |
|
= ∞, |
||||||
|
|
|
|
|
|||||||
|
1 |
3 |
1 |
|
|||||||
x→∞ |
|
|
|||||||||
|
|
|
− |
|
|
+ |
|
|
|
||
|
|
x2 |
x3 |
|
x4 |
|
|
||||
так как при x → ∞ числитель стремится к 1, а знаменатель к бесконечно малой величине, отсюда следует, что предел стремится к ∞.
Ответ:
lim |
|
x4 −5x |
|
= ∞. |
||
x |
2 |
−3x |
+1 |
|||
x→∞ |
|
|
||||
№286
РЕШЕНИЕ
Вычислить предел функции в точке х = ∞:
|
x |
3 |
|
|
x |
2 |
|
|
|
|
|
|
− |
|
|
|
|||
|
2 |
|
|
|
|
|
|||
lim |
2x |
−1 |
2x +1 |
. |
|||||
x→∞ |
|
|
|
||||||
В данном случае имеем неопределённость типа: ∞ - ∞. Для нахождения предела преобразуем данную разность в дробно – рациональную функцию Для нахождения предела преобразуем данную дробь, поделив числитель и знаменатель на x с большей степенью.
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
lim |
|
|
x3 + x2 |
|
= lim |
|
|
1+ x |
|
|
|
, |
|||
4x |
3 |
+ 2x |
2 |
− 2x −1 |
4 + |
2 |
− |
2 |
− |
1 |
|
||||
x→∞ |
|
|
x→∞ |
|
|
||||||||||
|
|
x |
x2 |
x3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

при x→∞ знаменатель стремится к 4, а числитель к 1, отсюда следует, что отношение стремится к 14 .
Ответ:
|
|
x |
3 |
|
|
x |
2 |
|
|
|
1 |
. |
|
|
|
|
|
− |
|
|
|
= |
|||||
|
|
2 |
|
|
|
|
|
|
|||||
lim |
2x |
−1 |
2x +1 |
|
4 |
||||||||
x→∞ |
|
|
|
|
|
|
|||||||
№ 316 Вычислить предел функции в точке х = 0:
lim sinαx .
x→0 sin βx
РЕШЕНИЕ По первому замечательному пределу
lim |
sin(αx) |
|
= lim α x |
= |
α . |
||||
sin(βx) |
|||||||||
x→0 |
|
x→0 |
β x |
|
β |
||||
Ответ: |
|
|
|
|
|
|
|
|
|
sin(αx) |
|
|
α |
|
|
|
|
||
lim |
|
= |
|
. |
|
|
|
||
|
|
|
|
|
|
||||
x→0 sin(βx) |
|
|
β |
|
|
|
|
||
№317 Вычислить предел функции в точке х = 0:
lim tg2xx .
x→0 sin 5
По первому замечательному пределу
lim |
tg2x |
= lim |
sin 2x |
|
|
= limsin 2x |
lim |
1 |
= |
2 |
1 = |
2 . |
||
|
sin 5x cos 2x |
cos 2x |
5 |
|||||||||||
x→0 sin 5x |
x→0 |
x→0 sin 5x |
x→0 |
|
|
5 |
||||||||
Ответ: lim |
tg2x |
= |
2 . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
x→0 sin 5x |
5 |
|
|
|
|
|
|
|
|
||||

|
№324 |
|
Вычислить предел функции в точке х = 0: |
lim1 |
+ sin x − cos x . |
x→0 1 |
−sin x − cos x |
Подставляем по формуле 2sin 2x = 1- cos(x).
Находим предел по первому замечательному пределу.
|
1+ sin x − |
2sin |
x |
|
1+ x − |
x |
|
2 + x |
|
||||
lim |
2 |
|
= lim |
2 |
|
= lim |
= −1 |
||||||
1−sin x − 2sin |
x |
|
1− x − |
x |
|
− 2 + x |
|||||||
x→0 |
|
x→0 |
|
x→0 |
|
||||||||
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||
Ответ: lim1 |
+ sin x − cos x |
= −1. |
|
|
|
|
|
||||||
|
x→0 1 |
−sin x − cos x |
|
|
|
|
|
|
|
||||
№334 Вычислить предел функции в точке х = α :
|
y −α |
|
πy |
|
lim sin |
|
tg |
|
|
2 |
|
|||
y→α |
|
2α |
||
Делаем замену µ = y −α , тогда:
|
|
µ |
|
|
π(µ +α) |
|
|
µ |
|
π |
|
πµ |
|
|
|
|
µ |
|
πµ |
|
sin µ cos πµ |
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
2α |
|
|||||||||||||
lim sin |
|
|
tg |
|
= lim sin |
|
tg( |
|
+ |
|
) |
= lim |
− sin |
|
ctg |
|
= −lim |
= |
|||||||
2 |
2α |
2 |
2 |
2α |
2 |
|
πµ |
||||||||||||||||||
µ→0 |
|
|
|
|
µ→0 |
|
|
|
|
µ→0 |
|
|
|
2α |
µ→0 |
sin |
|
||||||||
|
|
|
|
µ |
|
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
2α |
|
|
|
sin |
|
|
|
πµ |
|
|
1 = −α . |
|
|
|
|
|
|
|
|
|
|
|
||||||
− lim |
|
2 |
|
limcos |
= −lim |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
πµ |
2α |
πµ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
µ→0 |
sin |
µ→0 |
µ→0 |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2∂ |
|
|
|
2α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
y −α |
|
πy |
|
Ответ: lim sin |
|
tg |
|
||
2 |
2α |
||||
y→α |
|
|
|||
= − α ..
π

Образец решения задач при отработке.
Электронный вариант выполнил студент 471 группы Черных Евгений.
Берман Г.Н. Сборник задач по математическому анализу. 1998 г.
№ 47 9). Найти область определения функции:
y =1− 
 1− x2 .
1− x2 .
Решение: используя свойства арифметического корня, получим
1− x2 ≥ 0 x2 ≤1 −1≤ x ≤1.
Ответ: D(y) = [−1;1].
11). Найти область определения функции:
y = 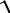
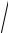 x2 −4x+3 .
x2 −4x+3 .
Решение: используя свойства арифметического корня, получим x2 − 4x + 3 ≥ 0, x2 − 4x + 3 = 0
x1 =1, x2 = 3,
тогда решениенеравенства иметвид: x (−∞;1] [3;+∞).
Ответ: D(y) = (−∞;1] [3;+∞) .
№ 48 12). Найти область определения функции:
|
|
|
|
|
|
1 |
|
|
y = x |
2 |
−3x + 2 + |
|
. |
||||
|
|
|
|
|||||
|
3 + 2x − x2 |
|||||||
Решение: используя свойства арифметического корня, получим
1

|
2 |
−3x + 2 ≥ 0 |
|
2 |
−3x + 2 ≥ 0 |
||
x |
|
x |
|
||||
|
|
|
|
|
|
|
|
|
+ 2x − x |
2 |
≥ 0 |
|
2 |
−2x −3 ≤ 0 |
|
3 |
|
x |
|
||||
решениемдвухнеравенств является :
[(−∞;1) (2;∞)] (−1;3) (−1;1) (2;3).
Ответ: D(y) = (−1;1) (2;3)..
13) Найти область определения функции:
y = 
 (x2 + x +1)−3 .
(x2 + x +1)−3 .
Решение: поскольку
x2 + x +1 > 0, для х R,
то решением является множество вещественных чисел.
Ответ: D(y) = (−∞;∞).
№ 306. Найти предел функции:
|
|
|
|
|
y = |
|
x + a |
− |
|
|
x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
при |
|
x →∞. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Решение: |
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
) ( |
|
|
|
|
|
) |
|
||||||||||||||
lim( |
|
|
|
|
|
)= lim |
|
|
|
|
− |
|
|
|
|
|
|
+ |
|
|
||||||||||||||||
|
|
− |
|
|
x + a |
|
x |
x + a |
x |
= |
||||||||||||||||||||||||||
x + a |
x |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x + a + |
|
x |
|||||||||||||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|||||||||||||||||||
= lim |
|
|
x + a − x |
= lim |
|
|
|
|
a |
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x + a + x |
|
x + a + x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x→∞ |
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Чтобы раскрыть неопределённость типа: - ∞, умножили на сопряжённое число, при делёнии любого конечного числа на бесконечность даёт ноль, поэтому предел равен нулю.
Ответ: lim(
 x + a −
x + a − 
 x )= 0.
x )= 0.
x→∞
2
№ 307. Найти предел функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = x2 +1 − x2 −1, |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
при |
|
x →∞. |
|
|
|
|
|
|
|
|
||||||
Решение: |
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
) ( |
|
|
|
|
)= |
||||||
lim( |
|
|
|
|
|
|
)= lim |
|
|
|
|
|
|
|
+ |
|
|||||||||||
|
|
|
|
|
|
|
|
x2 +1 − x2 |
−1 |
x2 |
+1 |
x2 −1 |
|||||||||||||||
x2 +1 − |
x2 −1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
x2 |
+1 + x2 |
−1 |
|||||||||
= lim |
2 |
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x→∞ |
|
|
x2 +1 + |
|
x2 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Применено умножение числителя и знаменателя на сопряжённое выражение числителю.
Ответ: lim(
 x2 +1 −
x2 +1 − 
 x2 −1)= 0.
x2 −1)= 0.
x→∞
№ 320. Найти предел функции:
y = |
2x − arcsin x |
, |
|
2x + arctgx |
|
при |
x → 0. |
|
Решение:
lim |
2x − arcsin x |
= lim |
2x − x |
= lim |
х |
= |
1 . |
|
2x + arctgx |
2x + x |
3х |
||||||
x→0 |
x→0 |
x→0 |
|
3 |
Использован первый замечательный предел.
Ответ:lim |
2x − arcsin x |
= |
1 . |
x→0 |
2x + arctgx |
|
3 |
3
№ 324. Найти предел функции:
y= 1+ sin x − cos x , 1−sin x − cos x
|
|
|
|
|
|
|
|
|
|
при x → 0. |
|
|
|
|
|
|
|
||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1+sin x −cos x = lim |
|
|
sin x + 2sin |
2 |
|
x |
|
|
|
|||||||||||||
lim |
|
|
|
2 |
|
|
= |
||||||||||||||||
|
|
|
|
|
2 x |
|
|||||||||||||||||
x→0 |
1−sin x −cos x |
|
x→0 |
−sin x + 2sin |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x + |
x2 |
|
|
1+ |
|
x |
|
|
2 + x |
|
|
|
|
|
|
|
|||||
= lim |
|
2 |
|
|
= lim |
|
2 |
|
= lim |
=1. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
x |
|
2 − x |
|
|
|||||||||||
x→0 |
− x + |
|
x2 |
|
x→0 |
1− |
|
|
x→0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Использован первый замечательный предел.
Ответ:lim 1+sin x −cos x =1. x→0 1−sin x −cos x
4
Практическое занятие №1
1. Организационные вопросы:
1). Аудиторная нагрузка:
Лекции 2 часа в неделю, практика 4 часа в неделю и самостоятельная работа 7 часов в неделю. Рассматриваемые вопросы на лекциях и на практических занятиях, составляют единый курс математического анализа и многие вопросы могут не пересекаться с вопросами, рассматриваемыми на лекциях с вопросами, рассматриваемыми на практике: результаты, полученные на лекциях будут использоваться на практических занятиях в предположении, что они уже усвоены студентами и наоборот результаты практических занятиях будут использоваться на лекциях. Поэтому ни в коем случае нельзя подразделять математику и в частности математический анализ на теорию и практику. Материал, изложенный на лекциях и практических занятиях в обязательном порядке должен обрабатываться дома, в соответствие с экзаменационными вопросами и в соответствии с логической последовательностью. Отсутствие студента на практическом занятии влечёт решение 6 задач, с оформлением решения на компьютере.
2). Контрольные мероприятия в семестре:
Самостоятельные работы по каждой теме, объявляются преподавателем заранее, контрольные работы раз в месяц и того 4 контрольные работы (по каждой самостоятельной работе и контрольной работе выставляется оценка в пятибалльной системе). Средняя арифметическая оценка по самостоятельным и контрольным работам будет выставляться на экзамене третьей оценкой по решению практических заданий. Студент, получивший положительную оценку по практическим занятиям, получает автоматически зачёт в зачётную книжку, студент, не получивший зачёта не допускается к экзамену. В конце семестра в экзаменационную сессию проводится экзамен по предмету, студенты, не сдавшие экзамен, имеют возможность ещё раз пересдать экзамен преподавателю в начале каникул (если даже студент не явился на экзамен), третья пересдача комиссии. После чего студент, не сдавший экзамен, отчисляется.
3). Литература (основная на первый семестр):
1.Шипачёв В.С. «Высшая математика» любого года издания.
2.Ильин В.А., Позняк Э.Г. «Основы математического анализа» Части 1 и 2 любого года издания.
3.Кудрявцев Л.Д. «Курс математического анализа» Том 1 и 2 любого года издания.
4.Фихтингольц Г.М. «Курс дифференциального и интегрального исчисления». Тома 1.2,3. Любого года издания.
5.Берман Г.Н. «Сборник задач по курсу математический анализ» (любого года издания сверяя номера задач по изданию 1971 г.).
1

2. Числа. Вещественные числа, операции над вещественными числами и их свойства.
Число – основное математическое понятие, являющееся количественной мерой (или мерой количества) чего-либо: предметов, отношений и т.п. Это понятие позволяющее ответить на вопросы: сколько?, на сколько?, во сколько? и т.д.
Понятие числа восходит от натуральных чисел, являющихся мерой количества предметов. При использовании арабского написания цифр, числа пишутся виде: 1,2,3,…,n,…,. Множество всех натуральных чисел (а их бесконечно много) записывают виде: N = {n: 1, 2, 3,…,m,m + 1,…,…,∞}. Построение множеств от множества натуральных чисел до множества комплексных чисел будет дано в лекциях. Сейчас запишем обозначения множеств, изученных в школе и интуитивные понятия которых у каждого есть. Множество всех целых чисел записывают виде:
Z = {-∞…, -n, - (n-1), …, -2, -1, 0, 1, 2, …, n, n+1, … , + ∞}.
Множество всех рациональных чисел записывают виде:
|
m |
|
Q = q = |
n |
: m Z n N . Множество всех вещественных чисел запи- |
|
|
сывают R.
На этих множествах вводят операции над числами, такие как сложение (+); вычитание (-); умножение ( ); деление (: = / ); возведение в степень
1
(хк); извлечение корней (m х = x m ). Эти операции изучаются в школе. Изучаются также законы, которым подчиняются данные операции: перестановочный закон = коммутативность операции; сочетательный закон = ассоциативность операции; распределительный закон = дистрибутивность одной операции относительно другой. Символически эти свойства операций записываются так
х = x m ). Эти операции изучаются в школе. Изучаются также законы, которым подчиняются данные операции: перестановочный закон = коммутативность операции; сочетательный закон = ассоциативность операции; распределительный закон = дистрибутивность одной операции относительно другой. Символически эти свойства операций записываются так
1.Коммутативность операции Т: х Т у = у Т х.
2.Ассоциативность операции Т: а Т (b T c) = (a T b) T c.
3.Дистрибутивность операции Т относительно операции Е:
р Т (е Е к) = (р Е е) Т (р Е к).
Самостоятельно дома вспомнить все свойства введённых выше операций на множестве вещественных чисел.
3. Модуль вещественного числа и его свойства.
Определение. Модулем вещественного числа (абсолютной величиной вещественного числа) х, обозначаемого | x | называется само число х, если оно положительно или равно 0, либо –х, если это число отрицательно:
|
|
x,если |
х ≥ 0, |
x |
|
||
= |
|
|
|
|
− х,если |
х < 0. |
|
|
|
|
|
Примеры: 1). |-7| = -(-7) = 7; 2). |13| = 13; 3). |π| = π .
2

Свойства модуля вещественного числа:
1.| x | ≥ 0, для х R – следует из определения.
2.| -x | = | x | - чётность модуля. Следует из определения.
3.| x | = а > 0 x = ±a. Следует из определения.
4.x ≤ a −a ≤ x ≤ a.
5.x ≥ a xx≤≥−aa a > 0.
6.− x ≤ x ≤ x.
7.| с x | = | с | | x |.
8.x ± y ≤ x + y .
9.x − y ≥ 
 x − y
x − y
 .
.
10.| х у | = | х | | у |.
11.xα = x α
12. xy = xy , y ≠ 0.
4. Геометрическая интерпретация модуля вещественного числа, расстояние между числами.
Геометрическая интерпретация модуля вещественного числа:
Модуль вещественного числа – расстояние этого числа от элемента 0 на вещественной прямой. Поэтому модуль вещественного числа обладает свойствами расстояния:
1). x − y = 0 x = y.
2). |
|
|
x − y |
|
|
= |
|
|
|
y − x |
|
симметричность. |
|||||||
|
|
|
|
|
|
||||||||||||||
3). |
|
|
x − y |
|
≤ |
|
x − z |
|
+ |
|
z − y |
|
неравенство треугольника. |
||||||
|
|
|
|
|
|
|
|||||||||||||
Доказательство: x − y = x − z + z − y ≤ x − z + z − y .
5.Уравнения и неравенства, содержащие неизвестную величину под знаком модуля. Метод интервалов.
Определение 1. Равенством называется математическое выражение, содержащее знак равенства: =.
Например, a = b; ϕ(x) = f(x); 4 = 3; -5 = (-1) 5; 2+2=4.
Определение 2. Неравенством называется математическое выражение, содержащее один из знаков: ≤, ≥, <, >, ≠ .
Например, a < b; ϕ(x) ≥ f(x); 4 > 3; -5 < (-1) 5; 2 + 2 ≠ 4.
3

Определение 3. Тождеством называется математическое выражение, содержащее знак тождественного равенства:≡(это выражение при любых значениях переменных, входящих в него верно).
Например, sin2x + cos2x ≡ 1; a2 – b2 ≡(a-b)(a+b); (a + b)2 = a2 +2ab + b2.
Определение 4. Уравнением называется математическое равенство, содержащее, по крайней мере, одну переменную величину, при некоторых значениях которой равенство обращается в тождество, при других значениях становится ложным равенством.
Например, | x | = 1 (это равенство становится тождеством при х = -1 и при х = 1, а для других значений это равенство неверно); х2 + у2 = 1 это уравнение содержит две переменные х и у, лежащих на единичной окружности (все точки с соответствующими координатами, а их бесконечно много, обращают равенство в тождество, а другие значения координат приводят к ложному равенству.
Рассмотрим решение уравнений и неравенств, содержащих неизвестную величину под знаком модуля.
Часто приходится решать уравнения вида:
n
∑αk fk (x) = 0 .
k=1
Для того, чтобы решить это уравнение необходимо раскрыть модули по определению, т.е. определить при каких значениях переменной каждая функция fk(x) > 0 и при каких значениях она отрицательна, что приводит к разбиению вещественной оси на интервалы, в каждом из которых известен знак функции fk(x), поэтому такой метод решения и носит название: метод интервалов.
Пример 1. Решить уравнение х−4 = х.
Решение: Поскольку под знаком модуля находятся линейные функции, то достаточно найти точки пересечения графиков этих функций с осью ОХ, т.е. решить уравнения х = 0 и х – 4 = 0, откуда две точки х1 = 0; х2 = 4 разбивают всю вещественную ось на три интервала:
|
|
0 |
4 |
|
1.х (−∞,0]: -х + 4 = -х, откуда 4 = 0 ложное равенство, следовательно х1 .
2.х (0,4] : -х + 4 = х, откуда х = 2 (0,4], следовательно х2 = 2.
3.х (4,+∞) : х – 4 = х, откуда -4 = 0 ложное равенство, следовательно, х3 .
Ответ: х = 2. Что подтверждается проверкой.
4

Пример 2. Решить уравнение х + х−4 = х+7. Применяем метод интервалов:
-7 0 4
1. х (−∞,−7] : -х –х + 4 = -х - 7, откуда х = 11 (−∞,−7], следовательно х1
.
2.х (−7,0]: -х –х + 4 = х + 7, откуда х = -1 (−7,0] , следовательно х2 = -1.
3.х (0,4] : х –х + 4 = х + 7, откуда х = -3 (0,4], следовательно х3 .
4.х (4,+∞) : х + х - 4 = х + 7, откуда х = 11 (4,+∞) , следовательно х4 = 11.
Ответ: х1 = -1, х2 = 11.
Пример 3. Решить неравенство х−2 ≤ 3 − х −7. Решение: Применим метод интервалов.
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
1. |
х (−∞,2]: -х + 2 ≤ 3 – х - 7, откуда 2 ≤ -7 |
– ложное неравенство, следова- |
||||
тельно, х (−∞,2] , следовательно х1 . |
|
|
|
|
||
2. |
х (2,3]: х – 2 ≤ -х + 3 – 7, откуда 2х ≤ -2 и х ≤ -1, тогда х (2,3] , следова- |
|||||
тельно, х2 . |
|
|
|
|
||
3. |
х (3,+∞) : х – 2 ≤ -3 + х – 7 и -2 ≤ -10 – ложное неравенство, следовательно, |
|||||
х3 .
Ответ: х (нет решений).
Пример 4. Решить неравенство х + 5 −2х > 3x +6. Решение: Применяем метод интервалов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2,5 |
||
-2 |
|||||
1. х (−∞,−2] : -х + 5 - 2х > -3x – 6, откуда 5 > -6, что верно, следовательно,
х1 (−∞,−2].
2. х (−2,0]: -х + 5 - 2х > 3x + 6, откуда -1 > 6х, тогда х < -1/6 и
|
−∞, |
−1 |
|
x2 |
|
1 |
|
x |
6 |
(−2,0] |
−2,− |
6 |
. |
||
|
|
|
|
|
|
5

3. х (0;2,5]: х + 5 - 2х > 3x + 6, откуда -1 > 4х, тогда х < -1/4 и x −∞, −41 (0;2,5] = x3 .
4. х (2,5;+∞) : х - 5 + 2х > 3x + 6, откуда -5 > 6, следовательно, х4 .
Ответ: |
|
−∞;− |
1 |
|
x |
6 |
. |
||
|
|
|
|
6. Домашнее задание.
1.Выучить все свойства модуля вещественного числа. По определению модуля дать доказательство всех свойств модуля вещественного числа (необходимо к экзамену).
2.Изучить все свойства арифметических операций над вещественными числами.
3.Решить следующие уравнения и неравенства:
1). |
|
|
|
х |
|
− |
|
|
3х−4 |
|
|
= |
|
|
|
7 − х |
|
|
−12. |
2). |
|
|
|
|
|
х |
|
|
+ |
|
|
|
х−4 |
|
+ |
|
|
|
х+7 |
|
+ |
|
1 |
|
−7х |
|
= 36. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3). |
|
|
|
|
|
2 − х |
|
−11 |
|
+ 3 |
|
|
|
= х. |
4). |
|
3х−2 |
|
|
≤ |
|
13 − х |
|
+7. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5). |
|
|
|
х |
|
+ |
|
2х−5 |
|
> |
|
3x +7 |
|
. |
6). 3 |
|
|
х |
|
− |
|
5 + 2х |
|
≥ |
|
3x +6 |
|
|
−56. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7). |
|
|
|
х+12 |
|
|
|
≤1. |
8). |
|
х+14 |
|
−20 + |
|
5 − х |
|
< |
|
x +6 |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 −8х |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
−1 |
|
+ x |
|
|
|
|
|
|
|
|
|
х −1. |
|||||||||||||||||||||||||||||||||||||||||||
9). |
|
|
|
|
|
х + 3 |
|
+1 |
|
− 3 |
|
< 42. |
|
|
|
|
|
|
> |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
10) . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. К следующему занятию иметь каждому распечатки программы, по крайней мере, на первый семестр и экзаменационные вопросы. Распечатку методички по элементам математической логики и теории множеств.
6
Практическое занятие №2
1. Проверка домашнего задания (частично):
Решить следующие уравнения и неравенства:
1). |
|
|
|
х |
|
− |
|
|
3х−4 |
|
|
= |
|
|
|
7 − х |
|
|
−12. |
2). |
|
|
|
|
|
х |
|
|
+ |
|
|
|
х−4 |
|
+ |
|
|
|
х+7 |
|
+ |
|
1 |
|
−7х |
|
= 36. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3). |
|
|
|
|
|
2 − х |
|
−11 |
|
+ 3 |
|
|
|
= х. |
4). |
|
3х−2 |
|
|
≤ |
|
13 − х |
|
+7. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5). |
|
|
|
х |
|
+ |
|
2х−5 |
|
> |
|
3x +7 |
|
. |
6). 3 |
|
|
х |
|
− |
|
5 + 2х |
|
≥ |
|
3x +6 |
|
|
−56. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7). |
|
|
|
х+12 |
|
|
|
≤1. |
8). |
|
х+14 |
|
−20 + |
|
5 − х |
|
< |
|
x +6 |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 −8х |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
−1 |
|
+ x |
|
|
|
|
|
|
|
|
|
х −1. |
|||||||||||||||||||||||||||||||||||||||||||
9). |
|
|
|
|
|
х + 3 |
|
+1 |
|
− 3 |
|
< 42. |
|
|
|
|
|
|
> |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
10) . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Закрепление материала по теме уравнения и неравенства с неизвестными под знаком модуля (линейные функции):
Пример 1. Решить уравнение х−4 + х+3 − 6 −3х = х + 5 − х − х−3.
Решение: Приведём данное уравнение к эквивалентному уравнению, используя свойства модуля:
х−4 + х+3 = х + х−5 + х−3.
Поскольку под знаком модуля находятся линейные функции, то достаточно найти точки пересечения графиков этих функций с осью ОХ, т.е. решить уравнения х = 0 и х – 4 = 0, х + 3 = 0, х – 3 = 0, х – 5 = 0, откуда пять точек – нулей линейных функций х1 = -3; х2 = 0; х3 = 3; х4 = 4; х5 = 5; разбивают всю вещественную ось на шесть интервалов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
|
0 |
3 |
4 |
5 |
|||
1. х (−∞,−3]: -х + 4 – х - 3 = -х –х + 5 – х + 3 , откуда х = 7 (−∞,−3] , следова-
тельно х1 .
2. х (−3,0] : -х + 4 + х + 3 = -х –х + 5 – х + 3 , откуда х = (1/3) (−3,0], следо-
вательно х2 .
3. х (0,3] : -х + 4 + х + 3 = х –х + 5 – х + 3 , откуда х = 1 (0,3], следовательно
х3 = 1.
4.х (3,4]: -х + 4 + х + 3 = х –х + 5 + х - 3 , откуда х = 5 (3,4], следовательно
х4 .
5.х (4,5]: х - 4 + х + 3 = х –х + 5 + х - 3 , откуда х = 3 (4,5] , следовательно
х5 .
6.х (5,+∞) : х - 4 + х + 3 = х + х - 5 + х - 3 , откуда х = 7 (5,+∞) , следователь-
но х6 = 7.
Ответ: х1 = 1; х2 = 7. Что подтверждается проверкой.
1

Пример 2. Решить уравнение 

 х − 4 −11 + 3 = х.
х − 4 −11 + 3 = х.
В силу свойств модуля: х ≥ 0 и тогда 
 х − 4 −11 = х − 3. Применяем метод интервалов:
х − 4 −11 = х − 3. Применяем метод интервалов:
4 1. х (0,4] , поскольку х ≥ 0 : х + 7 = х − 3. , откуда 7 = -3 – ложное равенство,
следовательно х1 .
2. х (4,+∞) : х −15 = х − 3, решаем также методом интервалов:
4 15
1). При х (4,15]:-х + 15 = х – 3 х = 9, следовательно х2 = 9.
2). При х (15,+∞) : х + 15 = х = -3, откуда 15 = -3 – ложное равенство, следовательно, х3 .
Ответ: х = 9.
Пример 3. Решить неравенство х−2 ≤ 
 3х+ 2 −1. Решение: Применим метод интервалов.
3х+ 2 −1. Решение: Применим метод интервалов.
|
|
2 |
-2/3 |
||
1. х (−∞,−2/3] : -х + 2 ≤ 3| х + 1| , откуда при х (−∞,−1] :-х + 2 ≤ -3х – 3
х≤ -2,5, следовательно, х (−∞,−2,5], и х1 (−∞,−2,5] ; при х (−1,−2/3] : -х + 2 ≤ 3х + 3 х ≥ -1/4 (−1,−2/3], следовательно, х1 (−∞,−2,5] .
2. |
х (−2/3;2]: -х + 2 ≤ 3| х + 1|, откуда при х [−2/3;2], следует, что х2 = -2/3 и |
х ≥ -1/4 (−2/3;2] х (−1/ 4;2] следовательно, х2 (−1/ 4;2]. |
|
3. |
х (2,+∞) : х – 2 ≤ 3х +3 и -2,5 ≤ х, следовательно, х3 (2,+∞) . |
Ответ: x (−∞,−2,5] {−2/3} (−1/ 4;+∞).
2

3.Уравнения и неравенства с неизвестными под знаком модуля (квадратичные функции). Метод интервалов:
Пример 1. Решить уравнение: х2 + 2x = x + 2x −5 . Применим метод интервалов:
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
0 |
2,5 |
|
1. |
|
х (−∞,−2] : х2 + 2х = -х - 2x + 5, откуда х2 + 5х - 5 = 0, тогда |
|||||||||||||||||
|
|
|
|
= −5 ±3 |
|
x1 = −5 +3 |
|
|
|
x2 = −5 +3 |
|
≈ 0,85. следовательно, |
|||||||
|
|
x1,2 |
5 |
5 |
|
≈ −5,85; |
5 |
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
= − |
5 +3 |
|
|
(−∞,−2]. |
|
|
|
|
|
|
|||||||
х |
|
5 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
х (−2,0]: -х2 - 2х = -х - 2x + 5, тогда х < -1/6 и |
|
|
|||||||||||||||
x |
|
|
|
−1 |
|
|
|
2,− |
1 |
|
|
|
|
||||||
−∞, |
6 |
(−2,0] x2 − |
6 |
. |
|
|
|
||||||||||||
3. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
х (0;2,5]: х + 5 - 2х > 3x + 6, откуда -1 > 4х, тогда х < -1/4 и |
||||||||||||||||||
x |
|
|
|
−1 |
|
|
|
|
|
. |
|
|
|
|
|||||
−∞, |
4 |
(0;2,5] = x3 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. |
|
х (2,5;+∞) : х - 5 + 2х > 3x + 6, откуда -5 > 6, следовательно, х4 . |
|||||||||||||||||
Ответ: |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
x −∞;− |
6 |
. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 2. Решить неравенство: х2 + 2x +3 ≤ x + x2 −9 .
Применим метод интервалов, поскольку х2 + 2х + 3 > 0 при любых х R, то неравенство можно переписать виде: х2 + 2x +3 ≤ x + x2 −9
-3 0 3
1. х (−∞,−3]: х2 + 2х + 3 ≤ -х + 2x - 9, откуда х2 + х + 12 ≤ 0 – ложное неравенство, тогда х1 .
3

2. х (−3,0] : х2 + 2х + 3 ≤ -х - 2x + 9, откуда х2 + 5х - 6 ≤ 0, по теореме Виета
находим корни уравнения х2 + 5х - 6 = 0: х1 = -6; х2 = 1, решения неравенства лежат в отрезке х [−6,1], следовательно, х2 [−3,0].
3. х (0,3] : х2 + 2х + 3 ≤ х - 2x + 9, откуда х2 + 3х - 6 ≤ 0, найдём корни уравнения х2 + 3х - 6 = 0:
x1,2 |
= |
−3 ± |
33 |
|
x1 = − |
3 + |
|
33 |
|
≈ −4,37; |
x2 |
= |
−3 + |
33 |
|
≈1,37, следовательно, ре- |
|||||||
2 |
|
|
|
2 |
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 + |
|
≤ х ≤ |
−3 + |
|
. |
||||||||||||||||
шения неравенства лежат меду корнямих1 ≤ х ≤ х2 |
− |
33 |
33 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
30, −3 +2
 33 .
33 .
4.х (3,+∞) : х2 + 2х + 3 ≤ х + 2x - 9, откуда х2 - х + 12 ≤ 0– ложное неравен-
ство, тогда х4 .
|
|
−3 + |
|
|
|
Ответ: |
33 |
||||
х −3, |
|
|
|
. |
|
2 |
|
|
|||
|
|
|
|
|
4. Домашнее задание.
1. Решить следующие уравнения и неравенства:
1). |
|
|
|
|
х |
|
− |
|
3х2 −4х+1 |
|
= |
|
|
|
7 − х |
|
−12. |
2). |
|
|
|
|
|
х2 −4 |
|
|
+ |
|
|
х−4 |
|
− |
|
х+7 |
|
= 36. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5). |
|
3) . |
|
|
|
х2 + 5х − 6 |
|
|
|
= 3 − х2. |
4). |
|
3х2 −2х−3 |
|
|
≤ |
|
13 − х |
|
+7. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
х2 −8х+15 |
|
+ |
|
2х−5 |
|
> |
|
x +7 |
|
. |
6). 3 |
|
|
|
|
х |
|
− |
|
5 + 2х |
|
≥ |
|
3x2 −13 |
|
−56. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7). |
|
|
|
|
|
х+12 |
|
≤ |
|
1−4х |
|
. |
|
|
8). |
|
х+14 |
|
−20 + |
|
5 − х2 |
|
< |
|
36x + 23. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 −8х |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 −1. |
|||||||||||||||||||||
9). |
|
|
|
|
|
х2 +3 |
|
+1 |
|
−3х |
|
< 42. |
|
|
10) . |
|
|
−9 |
|
+ 4x |
|
> |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Подготовка к самостоятельной работе на 60 минут.
3.Подготовить по методичке отображения множеств и элементарные функции, их свойства, графики из школьного материала.
4
Практическое занятие №3
1. Проверка домашнего задания (частично):
Решить следующие уравнения и неравенства:
1). |
|
|
|
|
х |
|
− |
|
3х2 −4х+1 |
|
= |
|
|
|
7 − х |
|
−12. |
2). |
|
|
|
|
|
х2 −4 |
|
|
+ |
|
|
х−4 |
|
− |
|
х+7 |
|
= 36. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5). |
|
3) . |
|
|
|
х2 + 5х − 6 |
|
|
|
= 3 − х2. |
4). |
|
3х2 −2х−3 |
|
|
≤ |
|
13 − х |
|
+7. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
х2 −8х+15 |
|
+ |
|
2х−5 |
|
> |
|
x +7 |
|
. |
6). 3 |
|
|
х |
|
− |
|
5 + 2х |
|
≥ |
|
3x2 −13 |
|
−56. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7). |
|
|
|
|
|
х+12 |
|
≤ |
|
1−4х |
|
. |
|
|
8). |
|
х+14 |
|
−20 + |
|
5 − х2 |
|
< |
|
36x + 23. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 −8х |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 −1. |
|||||||||||||||||||||
9). |
|
|
|
|
|
х2 +3 |
|
+1 |
|
−3х |
|
< 42. |
10). |
|
|
|
−9 |
|
+ 4x |
|
> |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Закрепление материала по теме уравнения и неравенства с неизвестным под знаком модуля (квадратичные функции):
Пример 1. Решить уравнение
Решение:
Применим метод интервалов.
х2 + 4х+3 = х −12х.
|
|
|
-3 |
|
|
|
|
|
-1 |
0 |
|||||
1. |
х (−∞,−3] (−1,0]: х2 + 4х + 3 = -х - 12х, откуда х2 + 17х + 3 = 0, следова- |
||||||||||||||
тельно х1 . |
= -х - 12х, откуда х2 - 9х - 3 = 0, откуда |
||||||||||||||
2. |
х (−3,−1] : |
-х2 - 4х - 3 |
|||||||||||||
|
|
9 ± |
|
|
|
9 − |
|
|
|
x2 = |
9 + |
|
|
≈ 9,32 следовательно х2 . |
|
|
x1,2 = |
93 |
|
x1 = |
93 |
|
≈ −0,32; |
93 |
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
2 |
х2 + 4х + 3 |
|
|
|
2 |
|
|
|
||||||
3. |
х (0,+∞) : |
= х - 12х, откуда х2 + 15х + 3 = 0, следовательно, |
|||||||||||||
х3 .
Ответ: х .
1
Пример 2. Решить неравенство: х2 + 1− х2 ≤ х−1 + 2. Применяем метод интервалов для эквивалентного неравенства
х2 + х2 −1 ≤ х−1 + 2.
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
|
≤ х ≤ |
−1+ |
|
|
|
, следовательно |
|
|
|
|
||||||||||||||||||||||||||
1. |
х (−∞,−1] : |
|
2х2 + x −4 |
≤ 0 − |
33 |
33 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
х − |
1+ |
|
|
|
;−1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. х (−1,1]: |
|
|
-х2 - х + 3 ≥ 1 – х2 , откуда х ≤ 2, следовательно, |
х2 (−1,1]. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− |
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
|
||||||
3. |
х (1,+∞) : |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
, следовательно, |
17 |
|||||||||||||||||||||
|
|
|
2х |
|
− x −2 ≤ 0 |
|
|
|
|
|
|
≤ х ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
х3 1, |
|
|
|
. |
||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1+ |
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
х |
|
33 |
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
− |
|
|
|
|
|
|
, |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 3. Решить уравнение: |
|
х2 + x |
|
= |
|
x |
|
− х |
|
+ |
|
x −5 |
|
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Применим метод интервалов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
-1 |
0 |
5 |
1.х (−∞,−1] : х2 + х = -2х - x + 5, откуда х2 + 4х - 5 = 0, тогда
х1 = -5, х2 = 1 следовательно, х1 = −5 (−∞,−1].
2.х (−1,0]: -х2 - х = -х - x + 5, тогда х2 = -5 – ложное равенство, следова-
тельно х2 . |
|
|
|
|
|
|
|
|
||||
3. |
х (0;5]: х2 + х = -x + 5, откуда х2 + 2х – 5 = 0, тогда |
|||||||||||
x1 = −1− |
|
≈ −3,45; |
|
x2 = −1+ |
|
≈1,45, следовательно, x3 = −1+ |
|
|
||||
6 |
6 |
|||||||||||
6. |
||||||||||||
4. |
х (5;+∞) : х2 - 5 = 0, откуда х1,2 |
= ± |
|
, следовательно, х4 . |
||||||||
5 |
||||||||||||
Ответ: x1 = −5, х2 = |
|
−1. |
|
|
|
|
|
|
||||
6 |
|
|
|
|
|
|
||||||
2

3.Алгебраическая форма комплексного числа и операции над комплексными числами
Комплексные числа возникают при решении простейшего уравнения
х2 +1 = 0, откуда x1,2 = ±i , где i = 
 −1 . Алгебраическая форма комплексного
−1 . Алгебраическая форма комплексного
числа имеет вид z = x + y∙i. Геометрический образ комплексного числа и множества комплексных чисел.
Операции над комплексными числами в алгебраической форме. Операция сопряжения комплексного числа и её свойства:
z = x + y∙i; z* = x - y∙i.
1. (z*)* = z; 2. (z1 + z2)* = z1* + z2* ; 3. (a∙z)* = a∙z*; 4. x* = x; 5. (z1 z2 )* = z1* z2* ;
6. |
|
z1 |
* |
|
z* |
; 7 z∙z |
* |
= |z|, где |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||||||||
|
|
= |
1 |
z |
= |
x |
+ y |
. |
|||||||
|
|
|
|
|
|||||||||||
|
|
|
* |
|
|
|
|||||||||
|
z2 |
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
Операция деления комплексных чисел сводится к операции умножения с использованием операции сопряжения:
Пусть z1 = x1 + y1∙i; z2 = x2 + y2∙I, тогда z = |
z1 |
= |
x1 + y1 i |
= |
(x1 + y1 i)(x2 − y2 i) |
. |
z2 |
x2 + y2 i |
|
||||
|
|
|
x2 + y2 |
|||
4.Домашнее задание.
1.Все домашние задания, которые были заданы, решить.
2.Подготовка к самостоятельной работе на 60 минут.
3.Материал по комплексным числам разобрать и рассмотреть примеры на операции над комплексными числами.
4.Подготовить по методичке отображения множеств и элементарные функции, их свойства, графики из школьного материала.
3

Самостоятельная работа № 1.
Вариант № 1
1. Решить уравнение: x + x −7 − х+8 = 3.
2.Решить уравнение: x − x2 − 2x + 3 = x + 3.
3.Решить неравенство: х−3 ≥ x −7 + 4 − х .
4.Решить неравенство: 
 x2 −4х+ 4 −3x ≤ x +1 .
x2 −4х+ 4 −3x ≤ x +1 .
Самостоятельная работа № 1.
Вариант № 2
1.Решить уравнение: 3x + 2 − 7x −1 = 2х− х.
2.Решить уравнение: x2 + x − 5 − 2x − 5 = 4 − x .
3.Решить неравенство: х−3 > 7x −1 − x + 2х+1 .
4.Решить неравенство: 
 x2 −16 + 3x ≤ x −18.
x2 −16 + 3x ≤ x −18.
Самостоятельная работа № 1.
Вариант № 3
1.Решить уравнение: x +5х− 2 = x −7.
2.Решить уравнение: x − x2 + 2x + 3 = x − 3.
3.Решить неравенство: 5х+ 2 < 7 −3x − x
4.Решить неравенство: 
 x2 − 25 − x ≤ x −10 .
x2 − 25 − x ≤ x −10 .
Самостоятельная работа № 1.
Вариант № 4
1. Решить уравнение: 4x −1 − 3 − x = х.
2. Решить уравнение: 
 x + 24 −3x2 = 3.
x + 24 −3x2 = 3.
3.Решить неравенство: 5х−2 < 2 −7x + x .
4.Решить неравенство: 
 x2 − 4x + 2 + x ≤ 7 − 2x .
x2 − 4x + 2 + x ≤ 7 − 2x .
Самостоятельная работа № 1.
Вариант № 5
1.Решить уравнение: x −5 = 5 − х+ 2 х.
2.Решить уравнение: x − x2 + 2x + 3 = x2 + 3x − 24 .
3.Решить неравенство: х+12 ≤ 4 − x + x − х.
4.Решить неравенство: 
 x2 − 9 + 3x ≤ x − 6 .
x2 − 9 + 3x ≤ x − 6 .
Самостоятельная работа № 1.
Вариант № 6
1. Решить уравнение: x − 4 − 2 − х = 3х+ х.
2.Решить уравнение: x2 + x + x − 6 = x + 3.
3.Решить неравенство: х + 2 < x − 3 − 2х .
4.Решить неравенство: 
 x2 −1 + x ≤ 3x − 4 .
x2 −1 + x ≤ 3x − 4 .
Самостоятельная работа № 1.
Вариант № 7
1. Решить уравнение: 3x + 2 = х−7 − х.
2.Решить уравнение: x2 −2x + 3x −6 = x +3.
3.Решить неравенство: 
 х + 2 − 4х <1.
х + 2 − 4х <1.
4.Решить неравенство: 
 x2 −9 +3x ≤ 3x + 4 .
x2 −9 +3x ≤ 3x + 4 .
Самостоятельная работа № 1.
Вариант № 8
1. Решить уравнение: 2x −1 = 3 − х − х.
2.Решить уравнение: x2 − x −5 − x −5 = 4 − x .
3.Решить неравенство: x + 5 − x − 7 < x .
4.Решить неравенство: 
 x2 −1 + 2x ≤ x −8.
x2 −1 + 2x ≤ x −8.

Самостоятельная работа № 1.
Вариант № 9
1. Решить уравнение: х −3 2 − x = х− 4 + х.
2.Решить уравнение: x2 − x + x − 2 = x − 3.
3.Решить неравенство: x − 2 ≥ х− 2 + х.
4.Решить неравенство: 
 x2 − 9 + x ≤ x − 9 .
x2 − 9 + x ≤ x − 9 .
Самостоятельная работа № 1.
Вариант № 10
1. |
Решить уравнение: |
|
х+ 7 |
|
+ 4 |
|
2 − x |
|
= |
|
4х−1. |
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
x + 24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2. |
Решить уравнение: |
|
|
|
|
|
|
−3 |
= 3x . |
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
3. |
Решить неравенство: |
|
x −7 |
|
> |
|
х−3 |
|
+ |
|
|
|
2 +3х |
|
. |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
+ x ≥ |
|
5 − 2x |
|
. |
||||||||||||||||||||||||
4. |
Решить неравенство: |
|
|
x2 − 6x + 8 |
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
Самостоятельная работа № 1.
Вариант № 11
1. |
Решить уравнение: |
|
х− 4 |
|
− |
|
x |
|
= |
|
2х+1. |
|||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2. |
Решить уравнение: |
|
x − x2 |
|
+ |
|
x − 2 |
|
|
= x2 + 3x − 4. |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Решить неравенство: |
|
|
x + 2 |
|
> |
|
х |
|
− |
|
х−3 |
|
|
+ |
|
2х+3. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
+ 6x ≥ |
|
x − 6 |
|
. |
||||||||||||||||||||||||||||
4. |
Решить неравенство: |
|
|
|
x2 − 4 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Самостоятельная работа № 1. |
||||||||||||||||||||
|
Вариант № 12 |
||||||||||||||||||||
1. |
Решить уравнение: |
|
х+5 |
|
− |
|
x −7 |
|
+ |
|
х |
|
= 4. |
||||||||
|
|
|
|
|
|
||||||||||||||||
2. |
Решить уравнение: |
|
x − x2 |
|
− |
|
x − 2 |
|
= x2 − 3x + 4. |
||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Решить неравенство: x −11 ≥ х+ 2 − х−3.
4.Решить неравенство: 
 x2 − 4 − x ≥ x +1 .
x2 − 4 − x ≥ x +1 .

Самостоятельная работа № 1.
Вариант № 13
1. Решить уравнение: х+5 + x −7 = 2 х.
2.Решить уравнение: x2 −5x −5 − x − 7 = 4 +16x .
3.Решить неравенство: x −3 > х + 7.
4.Решить неравенство: 
 x2 −1 + 2 ≤ x −8.
x2 −1 + 2 ≤ x −8.
Самостоятельная работа № 1.
Вариант № 14
1.Решить уравнение: х− 2 − 5 − x = 4.
2.Решить уравнение: x2 − x + 5x − 2 = 24x − 3.
3. |
Решить неравенство: |
|
x − 2 |
|
≤ |
|
х−7 |
|
+ |
|
х+1. |
||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
− 6 ≤ |
|
x − 9 |
|
. |
||||||||
4. |
Решить неравенство: |
|
|
x2 − 9 |
|||||||||||||
|
|
|
|
||||||||||||||
Самостоятельная работа № 1.
Вариант № 15
1. |
Решить уравнение: |
|
|
х−7 |
|
|
− |
|
x −3 |
|
|
=10 + |
|
х |
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2. |
Решить уравнение: |
|
|
|
x −4 |
|
|
|
−3х |
|
|
|
= 3x . |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
3. |
Решить неравенство: |
|
|
|
x |
|
≥ |
|
х− 4 |
|
− |
|
х−3. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
− 7 ≥ |
|
5 − 2x |
|
. |
|||||||||||||||||||||||
4. |
Решить неравенство: |
|
|
|
|
x2 − 6x + 8 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Самостоятельная работа № 1.
Вариант № 16
1. |
Решить уравнение: |
|
|
х−7 |
|
− |
|
|
x |
|
= |
|
х+8 |
|
− 4. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
2. |
Решить уравнение: |
|
1+ x − x2 |
|
+ |
|
x +12 |
|
= x2 −3x −12 . |
||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
3. |
Решить неравенство: |
|
|
|
x +3 |
|
≤ |
|
х− 2 |
|
− |
|
х |
|
+5. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
+ 6x ≥ |
|
4 − 6х |
|
. |
||||||||||||||||||||||||||
4. |
Решить неравенство: |
|
|
|
|
x2 − 4 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||

Самостоятельная работа № 1.
Вариант № 17
1. |
Решить уравнение: |
|
|
|
|
х− |
|
2 − х |
|
|
|
= 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x − x2 |
|
|
+ |
|
|
|
|
|
|
|
x −15 |
|
|
|
|
|
|
|
|
|
|
|
|
= x2 − 3x + 4 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. |
Решить уравнение: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Решить неравенство: |
|
|
|
|
|
x |
|
− |
|
|
|
|
|
2 −3х |
|
< |
|
|
|
|
|
|
|
|
|
|
|
х+5 |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−12 ≥ |
|
|
|
|
3x + 4 |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
Решить неравенство: |
|
|
|
|
|
|
|
|
|
x2 − 4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Самостоятельная работа № 1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант № 18 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
х+ 7 |
|
|
|
|
|
− |
|
|
|
|
2 − х |
|
= |
|
х |
|
|
|
|
|
− 24. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. |
Решить уравнение: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 + x |
|
− |
|
|
|
x − 2 |
|
|
|
= 3x + 4 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. |
Решить уравнение: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Решить уравнение: |
|
|
|
|
|
|
x |
|
|
− 4х + 2 |
|
|
|
<1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 5x ≤ |
|
3x +14 |
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
Решить неравенство: |
|
|
|
|
|
|
|
|
|
x2 −1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Самостоятельная работа № 1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант № 19 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. |
Решить уравнение: |
|
|
|
|
х+ 7 |
|
− |
|
15 − х |
|
|
= |
|
|
|
|
|
х |
|
+ 24. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x2 −2x |
|
|
|
− |
|
x −2 |
|
|
|
|
= 2x + 4 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. |
Решить уравнение: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. |
Решить уравнение: |
|
|
|
|
|
|
x |
|
|
+ 4х + 2 |
|
|
≥1. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
Решить неравенство: |
|
|
|
|
|
|
|
|
|
x2 −1 −5x ≤ |
|
|
x + 4 |
|
. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Самостоятельная работа № 1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант № 20 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. |
Решить уравнение: |
|
|
|
|
х−17 |
|
− |
|
5 − х |
|
= 7 |
|
х |
|
− 24. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x2 −2x + 2 |
|
|
|
− |
|
x −2 |
|
|
|
= 2x +1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. |
Решить уравнение: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. |
Решить уравнение: |
|
|
|
|
|
x |
|
|
− 4х − 2 |
|
≥ 7 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
Решить неравенство: |
|
|
|
|
|
|
|
|
|
x2 −1 +5 ≤ |
|
x + 4 |
|
− х. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
Самостоятельная работа № 1. |
|||||||||||||||||
|
Вариант № 21 |
|||||||||||||||||
1. |
Решить уравнение: |
|
|
х |
|
|
|
− |
|
1− х |
|
= |
|
х |
|
− 4х. |
||
|
|
|
|
|
|
|
||||||||||||
2. |
Решить равнение: |
|
1− |
|
x + 24 |
|
= 3x +11. |
|||||||||||
|
|
|
||||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Решить неравенство: 
 x − 4х − 2 ≥ 7 + х .
x − 4х − 2 ≥ 7 + х .
4.Решить неравенство: 
 x2 − 6x + 8 + 3x ≥ 1− 2x .
x2 − 6x + 8 + 3x ≥ 1− 2x .
Самостоятельная работа № 1.
Вариант № 22
1.Решить уравнение: х−1 + 1− х = х +1.
2.Решить равнение: x − x2 − 5x − 2 = x2 + 3x − 7 .
3.Решить неравенство: 
 x + 4 − 4х − 2 ≥ 1+ х .
x + 4 − 4х − 2 ≥ 1+ х .
4.Решить неравенство: 
 x2 −6x +8 −3x ≥ 1−2x .
x2 −6x +8 −3x ≥ 1−2x .
Самостоятельная работа № 1.
Вариант № 23
1. |
Решить уравнение: |
|
х−3 |
|
+ |
|
1− 2х |
|
= |
|
х+3 |
|
+1. |
||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
x −3x2 |
|
+ |
|
2x −3 |
|
= x2 −3x −4 . |
||||||||||
2. |
Решить уравнение: |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Решить неравенство: 
 x − 4 + 4х − 2 ≥ 1+ 3х .
x − 4 + 4х − 2 ≥ 1+ 3х .
4.Решить неравенство: 
 x2 −4 −2 ≥ 3x + 4 .
x2 −4 −2 ≥ 3x + 4 .
Самостоятельная работа № 1.
Вариант № 24
1. |
Решить уравнение: |
|
х−3 |
|
− |
|
3 − 2х |
|
= |
|
х+3 |
|
−1. |
||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
2x +3x2 |
|
− |
|
x −3 |
|
= x2 −5x + 4 . |
||||||||||
2. |
Решить уравнение: |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Решить неравенство: 
 x + 4х + 2 ≥ 1−3х .
x + 4х + 2 ≥ 1−3х .
4.Решить неравенство: 
 x2 −4 + 2 ≥ x + 4 .
x2 −4 + 2 ≥ x + 4 .

Самостоятельная работа № 1.
Вариант № 25
1. |
Решить уравнение: |
|
х+3 |
|
+ |
|
|
|
3 − 2х |
|
= |
|
х−5 |
|
−16. |
||||
|
|
|
|
|
|
||||||||||||||
|
|
|
2x −3x2 |
|
+ |
|
x − 2 |
|
= x2 +5x + 4 . |
||||||||||
2. |
Решить уравнение: |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Решить неравенство: 
 x −5 + 4х ≥ 5 −3х .
x −5 + 4х ≥ 5 −3х .
4.Решить неравенство: 
 x2 −9 ≥ x + 4 −3 .
x2 −9 ≥ x + 4 −3 .
Самостоятельная работа № 1.
Вариант № 26
1. Решить уравнение: 4х−3 − 3 + 4х = х−3 −1.
2.Решить уравнение: 1+ 2x +3x2 − x −1 = x2 − x − 4 .
3.Решить неравенство: 
 x + 4х + 2 ≤ 1−3х .
x + 4х + 2 ≤ 1−3х .
4.Решить неравенство: 
 x2 − 4х+ 4 + 2 ≥ x2 − 4 .
x2 − 4х+ 4 + 2 ≥ x2 − 4 .
Самостоятельная работа № 1.
Вариант № 27
1. |
Решить уравнение: |
3 |
|
х |
|
− |
|
3 − 2х |
|
= |
|
х+3 |
|
−18. |
|||||||
|
|
|
|
|
|
||||||||||||||||
2. |
Решить уравнение: |
|
2x + x2 |
|
+ |
|
x −3 |
|
= x2 − 4x + 4 . |
||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Решить неравенство: 5 − x
 ≥ 1−3х − х .
≥ 1−3х − х .
4.Решить неравенство: 
 x2 − 4х +12 ≥ x + 4 .
x2 − 4х +12 ≥ x + 4 .
Самостоятельная работа № 1.
Вариант № 28
1. Решить уравнение: х−3 + 3 − 2х = х−7 +1.
2.Решить уравнение: 2x + x2 − x +3 = x2 − x + 4 .
3.Решить неравенство: 3 x + х − 2 ≥ 1+ 3х .
4.Решить неравенство: 
 x2 − 2х −8 ≥ x + 4 −16 .
x2 − 2х −8 ≥ x + 4 −16 .
Самостоятельная работа № 2 Вариант № 1
1. Вычислить:
[(1− i)2 + (1+ i)−2 ]3 (4 − 3i)* 12 − 5i
2. Записать в тригонометрической форме комплексные числа:
1). z = 4 – 3i; 2). z = – 3i; 3). z = -1.
3. Извлечь корень кубический на множестве комплексных чисел:
1). z = 
 3 − i.
3 − i.
Сделать проверку.
Самостоятельная работа № 2 Вариант № 2
1. Вычислить:
[(3 + i)2 + (1+ 5i)2 ]−3 (4 + 3i)* 2 − 
 5 i
5 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 – 3i; 2). z = 2i; 3). z = -3. 3. Вычислить:
|
2 −5i |
|
i |
27 |
|
−2 |
|
|
|
−2 |
|
|
+1 . |
||
2 +5i |
|
||||||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 3
1. Вычислить:
[(1− i)3 − (1+ i)2 ]2 (1− 2i)* 2 − 
 14 i
14 i
2. Записать в тригонометрической форме комплексные числа:
1). z = -1 + i; 2). z = 1+7 i; 3). z = -2.
3. Извлечь корень кубический на множестве комплексных чисел:
1). z = 
 3 i.
3 i.
Сделать проверку.
Самостоятельная работа № 2 Вариант № 4
1. Вычислить:
[(2 −3i)2 + (1−5i)2 ]−3 (2 + 3i)* 2
 11 −
11 − 
 5 i
5 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 – 3i; 2). z = -5i; 3). z = 3. 3. Вычислить:
|
2 −i |
|
i |
77 |
|
−2 |
|
|
|
−4 |
|
|
+1 . |
||
2 +i |
|
||||||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 5
1. Вычислить:
[(1+ i)3 + (1−i)3 ]2 (3 −8i)* 12 − 2
 13 i
13 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 +13i; 2). z = -5i; 3). z = 11. 3. Вычислить:
|
1−5i |
−2 |
i |
121 |
|
−2 |
|
|
1+3i |
|
|
−1 . |
|||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 6
1. Вычислить:
[(1− i)3 − (1+ i)3 ]−2 (1+12i)* 

 2 −
2 − 
 14 i
14 i
2. Записать в тригонометрической форме комплексные числа:
1). z = -1 + i; 2). z = 1+ i; 3). z = -1.
3. Извлечь корень кубический на множестве комплексных чисел:
1). z = 
 3.
3.
Сделать проверку.
Самостоятельная работа № 2 Вариант № 7
1. Вычислить:
[(2 −3i)2 + (1−i)2 ]3 (3 −9i)* 2
 19 −
19 − 
 5 i .
5 i .
2. Записать в тригонометрической форме комплексные числа:
1). z = 7 – i; 2). z = 1-5i; 3). z = 3i. 3. Вычислить:
|
1−6i |
−3 |
i |
257 |
|
2 |
|
|
6 +i |
|
|
+1. |
|||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 8
1. Вычислить:
[(2 −3i)2 + (1−i)3 ]−2 (−1+ 3i)* 4
 11 − 2
11 − 2
 5 i
5 i
2. Записать в тригонометрической форме комплексные числа:
1). z = – 3i; 2). z = 7 - 5i; 3). z = -1. 3. Вычислить:
1−3i −4 i164  3 +i
3 +i
1. Вычислить:
2 +i .
Самостоятельная работа № 2 Вариант № 9
|
(1+i)3 |
|
|
2 |
|
2 |
* |
|
|
|
+ (1 |
−i) |
(−8i) |
|
12 −9 i |
||||||
|
|
|
|
|
||||||
2 −i |
|
|
||||||||
|
|
|
|
|
|
|
|
|
2. Записать в тригонометрической форме комплексные числа:
1). z = -4 + i; 2). z = -i; 3). z = 1. 3. Вычислить:
|
1−i |
− i |
131 |
|
−2 |
|
|
|
|
|
−1 . |
||
1+ 2i |
|
|||||
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 10
1. Вычислить:
[(1− i)3 + (1+ i)3 ]2 (1− 2i)* 

 27 −
27 − 
 33 i
33 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 - 13 i; 2). z = 11; 3). z = -1 + 3i.
3. Извлечь корень кубический на множестве комплексных чисел:
1). z = −1.
Сделать проверку.
Самостоятельная работа № 2 Вариант № 11
1. Вычислить:
[(2 −i)2 + (1−i)2 ]−3 (7 −9i)* 2
 30 −
30 − 
 5 i .
5 i .
2. Записать в тригонометрической форме комплексные числа:
1). z = 5 – i; 2). z = 1+6i; 3). z = -3i. 3. Вычислить:
|
1−i |
|
i |
57 |
|
2 |
|
|
|
−3 |
|
|
+1 . |
||
6 +3i |
|
||||||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 12
1. Вычислить:
(2 −3i)2 + (13−−5ii)2 3 (1−13i)* 

 7 −
7 − 
 2 i
2 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 3i; 2). z = -5i; 3). z = -4 + 3i. 3. Вычислить:
|
1−2i |
− i |
777 |
|
−2 |
|
|
2 +i |
|
|
+1 . |
||
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 13
1. Вычислить:
[(1+ i)3 + (1−i)3 ]3 (1−i)* 3 − 4
 10 i
10 i
2. Записать в тригонометрической форме комплексные числа:
1). z = -13 + 3i; 2). z = -i; 3). z = 1. 3. Вычислить:
|
(1−i)2 |
|
12 |
−2 |
|
|
|
|
−i |
|
|
−1 . |
|
|
|
|||||
|
1+3i |
|
|
|||
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 14
1. Вычислить:
[(1− i)−2 − (1+ i)2 ]3 (1−11i)* 

 22 −
22 − 
 14 i
14 i
2. Записать в тригонометрической форме комплексные числа:
1). z = -1 + 6i; 2). z = 6+ i; 3). z = -4.
3. Извлечь корень кубический на множестве комплексных чисел:
1). z = 
 3 +
3 + 
 22 i.
22 i.
Сделать проверку.
Самостоятельная работа № 2 Вариант № 15
1. Вычислить:
|
(2 −3i) |
2 |
2 |
|
|
|
|
|
|
||
(6 −9i)* |
19 − 6 i |
. |
|||||||||
|
|
+1 |
|||||||||
6 − 7i |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
2. Записать в тригонометрической форме комплексные числа:
1). z = 7 + i; 2). z = 1-7i; 3). z = 4i. 3. Вычислить:
|
1−26i |
−6 |
i |
254 |
|
2 |
|
|
26 +i |
|
|
−i . |
|||
|
|
|
|
|
|
|
|

Самостоятельная работа № 2 Вариант № 16
1. Вычислить:
[(2 −i)2 + (4 −5i)2 ]−1 (6 −11i)* 2
 23 − 2
23 − 2
 2 i
2 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 – 8i; 2). z = 9i; 3). z = -21. 3. Вычислить:
|
2 −3i |
|
i |
97 |
|
−2 |
|
|
|
−16 |
|
|
−1 . |
||
3 + 2i |
|
||||||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 17
1. Вычислить:
[3(1+ i)3 + 2(1−i)3 ] (3 −15i)* 12 −5 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 + 3i; 2). z = 2 -5i; 3). z = -1/2. 3. Вычислить:
|
1− |
|
|
|
i |
|
|
−2 |
|
|
|
|
5 |
|
163 |
|
|
||||
|
|
|
|
|
|
−5 i |
|
|
−2 . |
|
|
|
|
|
|
|
|||||
|
|
5 +i |
|
|
||||||
|
|
|
|
|
|
|
||||
Самостоятельная работа № 2 Вариант № 18
1. Вычислить:
[(1− i)3 + 2(1+ i)3 ]−2 (1− 2i)* 

 26 −
26 − 
 10 i
10 i
2. Записать в тригонометрической форме комплексные числа:
1). z = -1 - i; 2). z = 1+ i; 3). z = i -1.
3. Извлечь корень кубический на множестве комплексных чисел:
1). z = 
 3 − i.
3 − i.
Сделать проверку.
Самостоятельная работа № 2 Вариант № 19
1. Вычислить:
[5(2 −i)2 + (5 −i)2 ]2 (3 +11i)* 2
 39 − 2
39 − 2
 10 i .
10 i .
2. Записать в тригонометрической форме комплексные числа:
1). z = – i; 2). z = 11-5i; 3). z = i. 3. Вычислить:
|
1−i |
−3 |
i |
59 |
|
−2 |
|
|
|
|
|
+1. |
|||
6 +5i |
|
||||||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 20
1. Вычислить:
[2 −3i + (1−5i)2 ]3 (4 + 3i)* 2
 15 − 2 i
15 − 2 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 – 11i; 2). z = -i; 3). z = 5. 3. Вычислить:
|
1−i |
|
i |
625 |
|
−2 |
|
|
|
−4 |
|
|
−1 . |
||
2 +3i |
|
||||||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 21
1. Вычислить:
[(1+ i)3 − 2(1+ i)2 ]3 (1−8i)* 11− 2 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 + 14i; 2). z = 1 -5i; 3). z = 1. 3. Вычислить:
|
1+5i |
−3 |
i |
1212 |
|
2 |
|
|
1+3i |
|
|
−1 . |
|||
|
|
|
|
|
|
|
|

Самостоятельная работа № 2 Вариант № 22
1. Вычислить: |
|
|
|
|
|
|
|
|
|
|
|
[(1− i)3 − (1+ i)3 ]−2 |
|
|
* |
|
|
|
|
|
|
|
(1 |
+12i) |
|
|
2 − 14 i |
|||||
|
1−12i |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2. Записать в тригонометрической форме комплексные числа:
1). z = -1 + 4i; 2). z = -5 + i; 3). z = -13.
3. Извлечь корень кубический на множестве комплексных чисел:
1). z = 7 − 
 42 i.
42 i.
Сделать проверку.
|
Самостоятельная работа № 2 |
|||||||
|
|
|
|
Вариант № 23 |
||||
1. Вычислить: |
|
|
|
|
|
|
|
|
[(2 −3i)2 + (1−i)2 ]3 |
|
|
|
|
i |
|
. |
|
(3 −9i)* |
2 |
29 |
− |
5 |
|
|||
1+3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Записать в тригонометрической форме комплексные числа:
1). z = 7 – 11i; 2). z = 1 - i; 3). z = -3i. 3. Вычислить:

 (16−+ii)2 −3 i25 −2 −1 .
(16−+ii)2 −3 i25 −2 −1 .
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Вариант № 24 |
||||||
1. Вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
[(2 −3i) |
2 |
|
2 |
3 |
|
1 |
|
3 |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
+ (5 −5i) |
+ |
2 15 − 2 10 i |
||||||||||||||||
|
|
] |
|
2 |
4 |
i |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 – 15i; 2). z = -7i; 3). z = -2. 3. Вычислить:
2 −3i |
|
|
77 |
|
−2 |
|
|
|
|
−4 |
i |
|
|
+1 . |
|
3 + 2i |
|
||||||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 25
1. Вычислить:
[3(1+i)3 + 2(1−i)3 ]−2 (1− 4i)* 9 − 
 19 i
19 i
2. Записать в тригонометрической форме комплексные числа:
1). z = 1 + 3i; 2). z = 4 - 5i; 3). z = -1. 3. Вычислить:
|
3 −5i |
−2 |
i |
219 |
|
2 |
|
|
5 +3i |
|
|
−1 . |
|||
|
|
|
|
|
|
|
|
Самостоятельная работа № 2 Вариант № 26
1. Вычислить:
[4(1+ i)2 − (1+ i)3 ]2 (1+ i)* 

 22 −
22 − 
 42 i
42 i
2. Записать в тригонометрической форме комплексные числа:
1). z = -1 -3 i; 2). z = -1+4i; 3). z = 1.
3. Извлечь корень кубический на множестве комплексных чисел:
1). z =1+ i.
Сделать проверку.
|
Самостоятельная работа № 2 |
|||||||
|
|
|
Вариант № 27 |
|||||
1. Вычислить: |
|
|
|
|
|
|
|
|
[(2 −3i)2 + (1−i)2 ]3 |
|
|
|
|
i |
|
. |
|
(5 − 25i)* |
2 |
|
− |
|
|
|||
39 |
13 |
|||||||
1+5i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Записать в тригонометрической форме комплексные числа:
1). z = 3 – i; 2). z = 1 - 3i; 3). z = i. 3. Вычислить:
|
4 −6i |
−3 |
i |
256 |
|
2 |
|
|
3 + 2i |
|
|
+1 . |
|||
|
|
|
|
|
|
|
|

Самостоятельная работа №3 Вариант №1
1. Найти аn по первым элементам последовательности:
1; 32 ; 53; 74 ;...
и вычислить предел этой последовательности.
2. Пользуясь определением предела, доказать, что
lim |
n2 + n |
= −1 и найти номер последовательности при ε = 0,01. |
|||||||||||
1− n2 |
|||||||||||||
n→∞ |
|
|
|
|
|
|
|
|
|
|
|||
3. Последовательность задана рекуррентным соотношением: |
|||||||||||||
a =1, |
a |
n+1 |
= 4a |
n |
+ 3n−1, записать общую формулу n – го элемента |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|||
последовательности и найти её предел. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
||
|
|
|
|
|
n |
2 |
− 4n |
||||||
|
|
|
|
|
|
|
+ n |
||||||
4. Найти предел последовательности: |
|
|
|
|
|
|
. |
||||||
|
|
1− 2n |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Самостоятельная работа №3 Вариант №2
1.Найти аn по первым элементам последовательности:
−2;1;6;13;...
и вычислить предел этой последовательности.
2. Пользуясь определением предела, доказать что
lim |
n2 + n + 2 |
|
|
= |
1 |
|
и найти номер последовательности при ε = 0,0001. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
n→∞ |
|
2 n2 + 5 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||
3. Последовательность задана рекуррентным соотношением: |
|||||||||||||||||||
a =1, |
|
a |
n+1 |
= a |
n |
+ 3n , записать общую формулу n – го элемента |
|||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
последовательности и найти её предел. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
n |
3 |
− 4n + n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. Найти предел последовательности: |
|
|
|
|
|
|
. |
||||||||||||
|
|
n − 2n2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Самостоятельная работа №3 Вариант №3
1. Найти аn по первым элементам последовательности:
73 ;104 ;135 ;...
ивычислить предел этой последовательности.
2. Пользуясь определением предела, доказать что
lim |
n2 + |
n |
+ 2 |
|
= |
1 |
|
и найти номер последовательности при ε = 0,01. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
n→∞ |
|
2 n2 + 5n |
|
2 |
|
|
|
|
|||||||
3. Последовательность задана рекуррентным соотношением: |
|||||||||||||||
a =1, |
|
a |
n+1 |
= 2a |
n |
+ 5n , записать общую формулу n – го элемента |
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
последовательности и найти её предел. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + n − n |
2 |
4. Найти предел последовательности: |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 2n2 |
|
|
|
|
Самостоятельная работа №3 |
||||||
|
|
|
Вариант №4 |
||||||
1. |
Найти аn по первым элементам последовательности: |
||||||||
4 ; |
7 |
;10 |
;... |
|
|
|
|
|
|
5 |
6 |
7 |
|
|
|
|
|
|
|
и вычислить предел этой последовательности. |
|||||||||
2. |
Пользуясь определением предела, доказать что |
||||||||
|
|
lim cosn = 0 и найти номер последовательности при ε = 0,01. |
|||||||
|
|
n→∞ |
n |
||||||
3. |
Последовательность задана рекуррентным соотношением: |
||||||||
a1 |
=1, |
a2 = 2, an+2 = 4an+1 + 5an , записать общую формулу n – го элемента |
|||||||
последовательности и найти её предел. |
|||||||||
4. |
Найти предел последовательности: lim |
|
( |
|
− |
|
). |
||
n |
n +1 |
n |
|||||||
|
|
|
n→∞ |
||||||

Самостоятельная работа №3 Вариант №5
1. Найти аn по первым элементам последовательности:
42 ; 76 ; 1024 ;...
ивычислить предел этой последовательности.
2.Пользуясь определением предела, доказать что
lim |
|
1 |
|
= 0 и найти номер последовательности при ε = 0,0001. |
|||||
|
+ 2n +1 |
||||||||
n→∞ n3 |
|
|
|
|
|
|
|||
3. Последовательность задана рекуррентным соотношением: |
|||||||||
a1 = −1, |
a2 = 0, an+2 = 5an+1 + 6an , записать общую формулу n – го элемента |
||||||||
последовательности и найти её предел. |
|
|
|
|
|||||
|
|
|
|
|
2 + n |
2 |
|
n2 |
|
|
|
|
|
|
|
|
|
||
4. Найти предел последовательности: |
|
|
|
|
.. |
||||
3n − n2 |
|
||||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №3 Вариант №6
1. Найти аn по первым элементам последовательности:
16 ;1201 ; 50402 ;...
ивычислить предел этой последовательности.
2.Пользуясь определением предела, доказать что
lim n |
|
n +1 |
=1 и найти номер последовательности при ε = 0,0001. |
|||||||
n→∞ |
n3 +1 |
|
|
|
|
|
|
|
||
3. Последовательность задана рекуррентным соотношением: |
||||||||||
a = 4, |
a |
n+1 |
= a |
n |
+ 4n , записать общую формулу n – го элемента |
|||||
1 |
|
|
|
|
|
|
|
|
||
последовательности и найти её предел. |
|
|
||||||||
|
|
|
|
|
|
|
|
2 + 7n + n |
2 |
|
4. Найти предел последовательности: |
|
.. |
||||||||
|
|
|
|
|
|
|
|
9 + n + 2n2 |
|
|
Самостоятельная работа №3 Вариант №7
1. Найти аn по первым элементам последовательности:
16 ;1201 ; 50402 ;...
ивычислить предел этой последовательности.
2.Пользуясь определением предела, доказать что
|
lim sin |
n |
= 0 и найти номер последовательности при ε = 0,01. |
|||
|
n→∞ |
n |
|
|
|
|
|
|
|
|
|
|
|
3. |
Последовательность задана рекуррентным соотношением: |
|||||
|
a1 =1, a2 |
=1, an+2 = 3an+1 − 2an , записать общую формулу n – го элемента |
||||
|
последовательности и найти её предел. |
|||||
|
Найти предел последовательности: lim n2 (n − |
|
). |
|||
4. |
n2 +1 |
|||||
|
|
|
|
n→∞ |
||
Самостоятельная работа №3 Вариант №8
1. Найти аn по первым элементам последовательности:
12 ; 53 ;105 ;...
ивычислить предел этой последовательности.
2.Пользуясь определением предела, доказать что
lim |
1−3n2 + 4n |
= − |
3 |
и найти номер последовательности при ε = 0,0001. |
||||
2n2 −3n + 7 |
2 |
|||||||
n→∞ |
|
|
|
|
|
|||
3. Последовательность задана рекуррентным соотношением: |
||||||||
a1 = 2, |
a2 = 3, |
an+2 |
= 5an+1 − 6an , записать общую формулу n – го элемента |
|||||
последовательности и найти её предел. |
|
|
||||||
|
|
|
|
|
2 |
+ n |
n |
|
|
|
|
|
|
|
|||
4. Найти предел последовательности: |
3 |
|
. |
|||||
|
|
|
|
|
− n |
|
||
|
|
|
|
|
|
|
|
|

Самостоятельная работа №3 Вариант №9
1. Найти аn по первым элементам последовательности:
3;9;19;...
ивычислить предел этой последовательности.
2.Пользуясь определением предела, доказать что
|
lim sin |
|
n |
= 0 и найти номер последовательности при ε = 0,0001. |
||||||||||||
|
n→∞ n + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. |
Последовательность задана рекуррентным соотношением: |
|||||||||||||||
|
a = −2, |
a |
n |
+1 |
= a |
n |
− 2n , записать общую формулу n – го элемента |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
последовательности и найти её предел. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||||
4. |
Найти предел последовательности: |
|
|
|
|
|
|
|
.. |
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
n +1 + |
n |
||||||
Самостоятельная работа №3 Вариант №10
1.Найти аn по первым элементам последовательности:
−13;− 42 ;− 91 ;...
ивычислить предел этой последовательности.
2.Пользуясь определением предела, доказать что
|
lim |
(−1)n |
= 0 и найти номер последовательности при ε = 0,0001. |
|||||
|
|
|||||||
|
n→∞ |
2n |
||||||
3. |
Последовательность задана рекуррентным соотношением: |
|||||||
|
a1 = −1, |
a2 =1, an+2 = 3an+1 + 2an , записать общую формулу n – го элемента |
||||||
|
последовательности и найти её предел. |
|||||||
|
Найти предел последовательности: lim n( |
|
− |
|
). |
|||
4. |
n2 −1 |
n2 +1 |
||||||
|
|
|
|
n→∞ |
||||

Самостоятельная работа №3 Вариант №11
1. Найти аn по первым элементам последовательности:
24 ;− 54 ;− 86 ;...
ивычислить предел этой последовательности.
2.Пользуясь определением предела, доказать что
lim n |
|
n |
+ 2n +1 = − 1 и найти номер последовательности при ε = 0,0001. |
|||
|
|
|||||
n→∞ |
7n n + 4 |
7 |
|
|
||
3. Последовательность задана рекуррентным соотношением: |
||||||
a1 =1, |
a2 = 3, |
an+2 =12an+1 −11an , записать общую формулу n – го элемента |
||||
последовательности и найти её предел. |
|
|||||
|
|
|
|
|
−3 + n |
n |
|
|
|
|
|
|
|
4. Найти предел последовательности: |
|
. |
||||
|
|
|
|
|
3 + n |
|
|
|
|
|
|
|
|
Самостоятельная работа №3 Вариант №12
1. Найти аn по первым элементам последовательности:
32 ; 95 ; 1027 ;...
ивычислить предел этой последовательности.
2.Пользуясь определением предела, доказать что
3−n
lim 2 2
n→∞
= 0 и найти номер последовательности при ε = 0,0001.
3. Последовательность задана рекуррентным соотношением:
a1 = 3, an+1 = an − 2n+1, записать общую формулу n – го элемента последовательности и найти её предел.
4. Найти предел последовательности: {
 5n + 3 −
5n + 3 − 
 n − 4}.
n − 4}.

Самостоятельная работа №3 Вариант №13
1. Пользуясь определением предела, доказать что
|
lim |
(−1)n |
= 0 и найти номер последовательности при ε = 0,0001. |
||||||
|
|
|
|||||||
|
n→∞ n + 2n |
|
|
|
|
|
|
||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||
|
a1 = −1, |
a2 |
= 2, |
an+2 = 3an+1 + 2an , записать общую формулу n – го элемента |
|||||
|
последовательности и найти её предел. |
||||||||
|
Найти предел последовательности: lim n( |
|
− |
|
). |
||||
3. |
n2 + 4n −3 |
n2 − n +1 |
|||||||
|
|
|
|
|
n→∞ |
||||
|
|
|
|
|
Самостоятельная работа №3 |
||||
|
|
|
|
|
Вариант №14 |
||||
1. |
Пользуясь определением предела, доказать что |
||||||||
|
lim |
10n2 |
=10 и найти номер последовательности при ε = 0,0001. |
||||||
|
|
+1 |
|||||||
|
n→∞ n2 |
|
|
|
|
|
|
||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||
|
a1 =1, |
|
a2 = 3, |
an+2 = 6an+1 +15an , записать общую формулу n – го элемента |
|||||
|
последовательности и найти её предел. |
||||||||
1+
3. Найти предел последовательности: 3 +
|
|
|
|
|
|
|
n |
||
n |
||||
|
|
|||
|
|
|
. |
|
|
||||
|
|
|
|
|
n |
|
|||
|
|
|
|
|
Самостоятельная работа №3 Вариант №15
1. Пользуясь определением предела, доказать что
|
1 |
|
|
и найти номер последовательности при ε = 0,0001. |
||||||||
limsin |
|
= 0 |
||||||||||
|
||||||||||||
n→∞ |
n2 |
|
|
|
|
|
|
|
|
|
||
2. Последовательность задана рекуррентным соотношением: |
||||||||||||
a =1, |
a |
n+1 |
= 3a |
n |
− 2n+1, записать общую формулу n – го элемента |
|||||||
1 |
|
|
|
|
|
|
|
|
|
|||
последовательности и найти её предел. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
− ln n |
3 |
|
||
|
|
|
|
|
|
ln(n +1) |
|
|
||||
3. Найти предел последовательности: |
|
|
|
|
|
. |
||||||
|
n |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|

Самостоятельная работа №3 Вариант №16
1. Пользуясь определением предела, доказать что
|
|
|
1 |
|
и найти номер последовательности при ε |
= 0,0001. |
||||
|
lim cos |
|
=1 |
|||||||
|
n→∞ |
n |
|
|
|
|
|
|
|
|
2. |
Последовательность задана рекуррентным соотношением: |
|
|
|||||||
|
a1 =1, |
a2 |
= 4, |
an+2 = 9an+1 +10an , записать общую формулу n – го элемента |
||||||
|
последовательности и найти её предел. |
|
|
|||||||
|
Найти предел последовательности: lim n( |
|
− |
|
|
). |
||||
3. |
n2 + 4n + 3 |
n2 |
+ n +1 |
|||||||
|
|
|
|
|
n→∞ |
|
|
|||
Самостоятельная работа №3 Вариант №17
1. Пользуясь определением предела, доказать что
lim(0,88)n |
= 0 и найти номер последовательности при ε = 0,0001. |
||||
n→∞ |
|
|
|
|
|
2. Последовательность задана рекуррентным соотношением: |
|||||
a1 =1, a2 =1, |
an+2 = 2an+1 +15an , |
записать общую формулу n – го элемента |
|||
последовательности и найти её предел. |
|
||||
|
|
|
1+ n |
n |
|
|
|
|
|
||
3. Найти предел последовательности: |
|
|
|
. |
|
|
|||||
|
|
|
1+ 2n |
|
|
|
|
|
|
|
|
Самостоятельная работа №3 Вариант №18
1. Пользуясь определением предела, доказать что
|
|
|
3 |
|
|
|
|
||
|
limtg |
|
|
|
|
= 0 и найти номер последовательности при ε = 0,0001. |
|||
|
|
|
|
||||||
|
n→∞ |
n |
|
|
|
|
|||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||
|
a = 4, |
|
a |
n+1 |
= 3a |
n |
+ 2n+1, записать общую формулу n – го элемента |
||
|
1 |
|
|
|
|
|
|||
|
последовательности и найти её предел. |
||||||||
3. |
Найти предел последовательности: {n(ln(n + 2) − ln n)}. |
||||||||

|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
Вариант №19 |
|
|
|
|
|
|
1. |
Пользуясь определением предела, доказать что |
||||||||||||||||
|
|
|
2n + 5 |
|
= ln 2 и найти номер последовательности при ε = 0,0001. |
||||||||||||
|
lim ln |
n +1 |
|
||||||||||||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||||||||||
|
a1 =1, |
a2 |
= 3, |
|
|
an+2 = 8an+1 + 9an , записать общую формулу n – го элемента |
|||||||||||
|
последовательности и найти её предел. |
|
|
|
|
|
|
||||||||||
|
Найти предел последовательности: lim n( |
|
− |
|
). |
||||||||||||
3. |
n2 − n + 2 |
n2 + 2n − 4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
Вариант №20 |
|
|
|
|
|
|
1. |
Пользуясь определением предела, доказать что |
||||||||||||||||
|
lim |
|
n −1 |
|
|
|
= 0 и найти номер последовательности при ε = 0,0001. |
||||||||||
|
|
|
+ n +1 |
||||||||||||||
|
n→∞ n2 |
|
|
|
|
|
|
|
|
||||||||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||||||||||
|
a1 =1, |
a2 |
=1, |
|
an+2 = 3an+1 + 40an , записать общую формулу n – го элемента |
||||||||||||
|
последовательности и найти её предел. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||
3. |
|
|
|
|
|
|
|
|
|
|
4 + n |
|
|
||||
Найти предел последовательности: |
|
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n − 2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
Вариант №21 |
|
|
|
|
|
|
1. |
Пользуясь определением предела, доказать что |
||||||||||||||||
|
lim |
2n + 3n |
= 0 и найти номер последовательности при ε = 0,0001. |
||||||||||||||
|
|
||||||||||||||||
|
n→∞ |
6n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||||||||||
|
a = 0, |
a |
n+1 |
= 3a |
n |
− 4n+1, записать общую формулу n – го элемента |
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
последовательности и найти её предел. |
|
|
|
|
|
|
||||||||||
3. |
Найти предел последовательности: {n(ln(n + 3) − ln(n − 2))}. |
||||||||||||||||
Самостоятельная работа №3 Вариант №22
1. Пользуясь определением предела, доказать что
|
|
|
n + 5 |
|
= 4 и найти номер последовательности при ε = 0,0001. |
||||||
|
lim nln |
|
|||||||||
|
n→∞ |
|
n +1 |
|
|
|
|
|
|
||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||||
|
a1 =1, |
a2 =1, |
|
|
|
an+2 = 2an+1 + 5an , записать общую формулу n – го элемента |
|||||
|
последовательности и найти её предел. |
|
|
||||||||
|
Найти предел последовательности: lim n( |
|
− |
|
). |
||||||
3. |
n2 − 2n + 2 |
n2 − 2n − 4 |
|||||||||
|
|
|
|
|
|
|
n→∞ |
|
|
||
|
|
|
|
|
|
|
Самостоятельная работа №3 |
|
|
||
|
|
|
|
|
|
|
Вариант №23 |
|
|
||
1. |
Пользуясь определением предела, доказать что |
|
|
||||||||
|
lim |
|
n |
|
|
|
=1 и найти номер последовательности при ε = 0,0001. |
||||
|
|
|
|
|
|
||||||
|
n→∞ |
|
n 2 +1 |
|
|
|
|
|
|||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||||
|
a1 =1, |
a2 = −1, |
an+2 = an+1 +8an , записать общую формулу n – го элемента |
||||||||
|
последовательности и найти её предел. |
|
|
||||||||
4 + n 2n
3. Найти предел последовательности: n −3
.
Самостоятельная работа №3 Вариант №24
1. Пользуясь определением предела, доказать что
|
lim |
1 |
+ 2 |
6n |
= 2 и найти номер последовательности при ε = 0,0001. |
||
|
|
2 + 6n |
|||||
|
n→∞ |
|
|
|
|
||
2. |
Последовательность задана рекуррентным соотношением: |
||||||
|
a = −2, a |
n+1 |
= 5a |
n |
−3n+1, записать общую формулу n – го элемента |
||
|
1 |
|
|
|
|
||
|
последовательности и найти её предел. |
||||||
3. |
Найти предел последовательности: {2n(ln(n + 3) − ln(n + 2))}. |
||||||

Самостоятельная работа №3 Вариант №25
4. Пользуясь определением предела, доказать что
|
lim |
ln n2 |
|
= 0 и найти номер последовательности при ε = 0,0001. |
|||||||||||||||||||||
|
|
|
n |
|
|||||||||||||||||||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5. |
Последовательность задана рекуррентным соотношением: |
||||||||||||||||||||||||
|
a1 =1, |
|
|
|
a2 |
|
= 2, |
|
an+2 = 4an+1 + 21an , записать общую формулу n – го элемента |
||||||||||||||||
|
последовательности и найти её предел. |
|
|
|
|
|
|
||||||||||||||||||
|
Найти предел последовательности: lim n( |
|
|
|
− |
|
). |
||||||||||||||||||
6. |
|
n2 |
+ 2 |
n2 − 4 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №26 |
|
|
|
|
|
|
|
1. |
Пользуясь определением предела, доказать что |
||||||||||||||||||||||||
|
|
|
|
|
( |
|
|
+ |
|
|
|
)=1 и найти номер последовательности при ε = 0,0001. |
|||||||||||||
|
lim |
|
|
n |
n |
n +1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
n→∞ |
|
|
|
|
|
4n 2 |
+ 1 |
|
|
|
|
|
|
|
|
|
||||||||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||||||||||||||||||
|
a1 = −1, |
|
a2 = −1, |
|
|
an+2 = 6an+1 −8an , записать общую формулу n – го элемента |
|||||||||||||||||||
|
последовательности и найти её предел. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 6 + n |
2n |
|||||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Найти предел последовательности: |
n + |
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №27 |
|
|
|
|
|
|
|
1. |
Пользуясь определением предела, доказать что |
||||||||||||||||||||||||
|
lim |
|
|
1 |
|
|
= 0 и найти номер последовательности при ε = 0,0001. |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
n→∞ ln2 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. |
Последовательность задана рекуррентным соотношением: |
||||||||||||||||||||||||
|
a = −1, |
|
a |
n |
+1 |
= 7a |
n |
−3n , записать общую формулу n – го элемента |
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
последовательности и найти её предел. |
|
|
|
|
|
|
||||||||||||||||||
3. |
Найти предел последовательности: {n(ln(2n + 3) − ln(21n + 5))}. |
||||||||||||||||||||||||
Самостоятельная работа №4 Вариант №1
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|||||||
1. |
lim |
|
(x3 −1)2 |
, |
2. |
lim |
2х2 + 5х − 3 |
. |
3. |
lim |
cos3x − cos x |
||||
|
(1 − x)2 |
|
|
||||||||||||
|
x→1 |
|
|
|
х→−3 |
х + 3 |
|
n→0 |
x2 |
||||||
|
|
tgx −sin x |
|
|
e4x −1 |
|
|
|
|
|
2x + 3 |
2x−1 |
|||
4. |
lim |
5. |
lim |
, |
|
6. |
|
x+2 |
|||||||
|
x |
3 |
, |
tgx |
|
lim |
5x − 7 |
|
|||||||
|
х→0 |
|
|
|
|
х→0 |
|
|
|
x→∞ |
|
||||
Самостоятельная работа №4 Вариант №2
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|||||||
|
|
x3 −1 |
|
|
|
|
|
|
|
− 5 |
. |
|
lim |
sin x −tgx |
|
1. |
lim |
|
, |
2. |
lim |
|
2х + 7 |
3. |
|||||||
|
|
|
|
|
|
|
x3 |
||||||||
|
|
3 − х |
|||||||||||||
|
x→1 1 − х2 |
|
|
х→9 |
|
х→0 |
|||||||||
|
lim |
2arcsin x |
|
lim |
e−x −1 |
|
|
|
2x + 3 |
|
|
4. |
3x |
, 5. |
sin x |
, |
6. |
lim |
|
|
|||
2x − 7 |
|||||||||||
|
х→0 |
|
х→0 |
|
|
x→∞ |
|
2x−1
2
Самостоятельная работа №4 Вариант №3
Вычислить пределы функций: |
|
|
|
|
|
|
|
|||||||
|
|
x3 +1 |
|
|
|
|
|
−1 |
|
|
|
lim |
sin3 mx −sin3 nx |
|
1. |
lim |
, |
2. |
lim |
|
х |
|
. |
3. |
|||||
1 − х2 |
|
|
|
|
|
x3 |
||||||||
3 − |
|
8 + х |
||||||||||||
|
x→−1 |
|
|
х→1 |
|
|
|
|
х→0 |
|||||
|
lim |
2arcsin x − arctgx |
|
lim |
3x −1 |
|
|
2x + 3 |
|
||
4. |
|
|
|
, 5. |
|
, 6. |
lim |
|
|
||
3x |
2 |
+ 2x |
sin 2x |
2x + 7 |
|||||||
|
х→0 |
|
|
х→0 |
|
x→∞ |
|
||||
Самостоятельная работа №4 Вариант №4
Вычислить пределы функций:
6x+3 5
1. |
lim |
|
x3 −1 |
|
, |
2. |
lim |
|
2х |
− x |
. |
3. |
lim |
sin x |
|
|
|
||
|
|
|
|
|
|
cos x −1 |
|
|
|||||||||||
3 1 − х2 |
|
|
|||||||||||||||||
|
x→1 |
|
|
|
х→2 |
|
x − 2 |
|
|
х→0 |
|
|
|||||||
|
lim |
2arcsin x + arcsin 3x |
, 5. lim |
10x −1 |
|
|
x − 3 |
|
|||||||||||
4. |
|
|
|
|
x |
|
sin 3x |
, |
6. |
lim |
|
|
|
||||||
|
|
|
|
|
|
7 |
|||||||||||||
|
х→0 |
|
|
|
|
|
|
|
x→0 |
|
|
x→∞ x − |
|
||||||
2x−1 4
.

Самостоятельная работа №4 Вариант №5
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
3 |
|
|
|
3 |
|
−1 |
|
|
cos3x + cos x − 2 |
||
|
|
|
|
|
lim |
х |
, 3. |
lim |
|||||||||
1. |
lim |
|
|
|
− |
|
|
, 2. |
|
|
|
|
x2 |
||||
1 |
− х |
1 − х3 |
|
|
|
|
|||||||||||
4 |
х −1 |
||||||||||||||||
|
x→1 |
|
|
|
х→−3 |
|
х→0 |
||||||||||
|
lim tg |
2 |
x −sin |
2 |
x |
|
lim e |
x |
−1+ sin x |
|
x + 3 |
x |
|
4. |
|
|
, 5. |
|
, 6. |
lim |
|
|
|||||
|
|
|
|
||||||||||
х→0 |
|
x4 |
|
|
х→0 |
|
tgx |
x→∞ x −1 |
|
||||
Самостоятельная работа №4 Вариант №6
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+cos3x |
|
|
||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1. |
lim |
x |
− 5x − 6 |
, |
|
2. |
lim |
|
x |
− |
|
|
|
х |
|
, |
|
3. |
|
lim |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
2 |
6x |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
6 − х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
х −1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
x→6 |
|
|
|
|
|
|
|
х→1 |
|
|
|
|
|
|
|
х→π |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
5arcsin x − arcsin 2x |
|
|
|
|
|
|
|
|
lim |
23x |
|
−1 |
|
|
|
|
|
x +1 |
|
|
х |
|
|
|||||||||||||||||||||||||
4. |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
5. |
|
|
|
|
|
|
|
|
|
, |
6. |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
sin 3x |
|
2x + 3 |
|
|
|
||||||||||||||||||||||||||||||
|
х→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х→0 |
|
|
|
x→∞ |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Вычислить пределы функций: |
( |
|
|
|
−1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
8x3 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
sin4 mx −sin4 nx |
|
|||||||||||||||||||||||||||
|
lim |
|
|
|
lim |
|
х |
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1. |
x→1 |
1 − 4х2 , 2. |
х→1 |
(3 − |
|
8 + х)(х |
−1) |
|
3. |
|
х→0 |
|
|
x4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
2arcsin x + arctgx |
|
|
lim 3 |
3x |
−1−sin x |
|
|
|
2x − 3 |
x |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
lim |
2x |
− 5 |
|
|||||||||||||||||||||||||||||||||||||||||
4. |
х→0 |
|
|
|
|
|
3x2 + 6x |
, |
5. |
х→0 |
|
|
|
|
sin 2x |
|
, |
|
6. x→∞ |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 3x |
|
|
|
|||||||||||||||||
|
|
|
|
|
x3 |
|
−1 |
|
|
|
|
|
|
|
|
|
|
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1. |
lim |
|
|
|
|
, |
|
|
2. |
lim |
|
4х |
, |
|
|
|
|
3. |
|
lim |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 − 3 |
|
|
|
|
|
|
x − 4 |
|
|
|
|
|
|
cos x −1 |
|
|
||||||||||||||||||||||||||||||||||
|
х2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
x→1 |
|
|
|
|
|
х→4 |
|
|
|
|
|
|
|
|
|
|
|
|
х→0 |
|
|
||||||||||||||||||||||||||||
|
|
arctgx + arcsin 3x |
|
|
|
|
|
|
|
|
3x |
−1+ tgx |
|
|
|
4x |
− 3 |
|
2x−1 |
|
|
|||||||||||||||||||||||||||||
|
lim |
|
|
lim |
|
|
|
4 |
|
|
||||||||||||||||||||||||||||||||||||||||
4. |
|
|
|
|
|
|
4x |
|
, |
5. |
|
|
|
|
sin 3x |
|
, 6. |
|
lim |
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4x − 7 |
|
|
|||||||||||||||||||||||||||||||||||
|
х→0 |
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
||||||||||||||||||||||||

Самостоятельная работа №4 Вариант №9
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 − |
1 |
3 |
|
|
|
|
3 |
|
|
|
|
− |
|
|
|
|
|
sin2 x −tg 2 x |
|||||||
|
|
|
|
|
1 |
− |
х |
|
|
|
|
|
|||||||||||||||
1. |
lim |
x |
|
|
|
2. |
lim |
|
|
|
|
1 |
, |
3. |
lim |
|
|
|
|
4 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
, |
|
|
|
4 1− х −1 |
|
x→π (x −π) |
|||||||||||||||||
|
x→1 1 − х |
|
|
|
x→−1 |
|
|
|
|||||||||||||||||||
|
lim ln(1+ sin x) |
|
|
|
|
|
2 |
x |
−1 |
|
|
|
|
x − 4 |
|
2x |
|
||||||||||
|
|
|
lim |
|
|
|
|
|
|
lim |
|
|
|
|
|
||||||||||||
4. |
, |
5. |
|
|
|
|
|
, |
6. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
ln(1+ 2x) |
|
|
|
|
||||||||||||||||||||||
|
x→0 |
sin 4x |
|
|
x→0 |
|
|
x→∞ x −3 |
|
|
|
||||||||||||||||
Самостоятельная работа №4 Вариант №10
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−cos 4x |
|
|||||||||||||||||||
|
|
|
2x2 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1. |
lim |
, |
|
|
2. |
lim |
|
|
x − 3 |
|
9 − х |
, |
3. |
lim |
|
|||||||||||||||||||||||||||||
|
х − 0,5 |
|
|
|
|
|
|
3x −18 |
|
|
|
tg6x |
|
|
||||||||||||||||||||||||||||||
|
x→2 |
|
|
|
|
|
х→6 |
|
|
|
|
х→0 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
sin−2 x |
|
|
|
|
|
|
33x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 − 2х х |
|
|||||||||||||||
4. |
lim(cos x) |
|
|
, |
5. lim |
sin 3x |
, |
|
|
|
|
|
|
|
|
6. |
lim |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
х→0 |
|
|
|
|
|
|
|
|
х→0 |
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
2x − 53 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
Самостоятельная работа №4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
8x3 −1 |
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хsin x + cos x −1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х3 |
|
|
−1 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
2 |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
lim |
|
|
|
|
|
|
|||||||
1. |
x→12 |
1 |
− 4х |
|
|
, 2. |
х→1 (3 − |
|
|
8 + х)(х − |
1) |
|
3. |
|
х→0 |
|
ln(1+ x) − e2x +1 |
|||||||||||||||||||||||||||
|
|
arcsin x + arctgx |
|
|
|
|
|
|
|
|
|
|
5x −3 |
11x |
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
4. |
lim |
|
|
|
|
|
|
|
|
, |
|
|
|
5. |
lim |
|
|
|
|
|
|
|
|
|
|
, |
|
6. |
lim x(e x |
−1) . |
||||||||||||||
|
|
|
3x |
|
|
|
|
|
|
5x + 7 |
|
|
||||||||||||||||||||||||||||||||
|
х→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х→0 |
|
|
|
|
|
|
|
x→∞ |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
Самостоятельная работа №4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x3 |
− 5x + 6 |
|
|
|
|
|
|
|
|
|
х − |
|
|
|
|
|
sin4 3x |
|
|
|
|||||||||||||||||||||
1. |
lim |
|
, |
lim |
|
|
2 |
, |
|
|
3. |
lim |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(cos x −1)2 |
|
|
||||||||||||||||||||||||||||||||
x→3 |
|
x2 |
− 8x +15 |
2. х→4 |
x − 4 |
|
|
|
|
|
|
|
|
х→0 |
|
|
|
|||||||||||||||||||||||||||
4. |
lim |
3tgx |
− 2tgx |
, |
|
5. lim |
|
|
x3 |
|
, |
6. |
|
|
lim |
|
ln(x |
+1) −ln x |
|
. |
||||||||||||||||||||||||
|
arcsin x |
|
|
sin 3x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
х→0 |
|
|
|
|
х→0 |
|
|
|
|
|
|
|
|
|
|
x→∞ ln(x −4) −ln(x + 4) |
|
||||||||||||||||||||||||||

Самостоятельная работа №4 Вариант №13
Вычислить пределы функций:
1. |
lim |
x2 |
− 2 |
2x |
|
, 2. |
lim |
3 |
х +1 |
−1 |
|
, |
3. |
lim |
|||
|
|
|
|
|
(x +1) |
3 |
−1 |
||||||||||
|
2x − 2 |
||||||||||||||||
|
x→2 |
|
|
|
х→0 |
|
|
|
|
х→1 |
|||||||
ctg πx2
1− x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
+9 |
|
x2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
a |
x |
− a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||
|
lim(sin 3x)tg |
x |
|
5. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
4. |
|
, |
|
|
|
, |
|
|
|
|
|
|
|
6. |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
х→ |
π |
|
|
|
|
|
|
|
|
|
|
a(x −1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−6 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
х→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Вычислить пределы функций: |
Вариант №14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgx −sin x |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1. |
lim |
4x |
+ 6x − 4 |
, |
|
|
|
2. |
|
lim |
|
|
|
x − x |
, |
|
|
|
|
3. |
lim |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin |
3 |
2x |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
2х −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
1− 3 |
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
x→0,5 |
|
|
|
|
|
|
|
|
|
|
|
х→1 |
|
|
|
|
|
|
|
|
|
|
х→0 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
arcsin x − arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ х |
|
х |
|||||||||||||||||
|
lim |
|
|
|
|
|
|
|
ln(1+ e |
x |
) −ln(e |
x |
−1) |
|
|
|
|
|
3 |
|
||||||||||||||||||||||||||||||||||||||
4. |
|
|
|
|
|
|
|
|
|
|
|
, 5. |
lim |
|
|
|
, |
6. |
lim |
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
− 51 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 4) |
|
|
|||||||||||||||||||||||||||||||
|
х→0 |
|
|
|
|
|
|
|
|
|
|
|
х→∞ ln(2 + ex ) −ln(ex |
|
|
|
|
x→∞ x |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Вычислить пределы функций: |
Вариант №15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
x3 |
−1 |
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хsin x + cos x −1 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
3 |
x2 |
− 23 |
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. |
lim |
1− |
х |
2 |
|
, 2. |
lim |
|
x |
2 |
|
− 2x +1 |
|
|
|
. |
|
3. |
lim |
|
ln(1 |
− x) + e |
2x |
−1 |
|
|
|
|||||||||||||||||||||||||||||||
|
x→1 |
|
|
|
|
х→1 |
|
|
|
|
|
|
|
|
|
х→0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
arcsin3 x + arctg2 x |
|
|
|
|
|
|
|
|
x −3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−x |
|
|
|
|
lim(ln(ex |
− e−x ) − ln x). |
|||||||||||||||||||||||||||||||||||||||||
4. |
lim |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
, |
|
|
5. |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
, 6. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
||||||||||||||||||||||||||||||||||||
|
х→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х→0 x + |
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Самостоятельная работа №4 Вариант №16
Вычислить пределы функций: |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
− 5x + 6 |
|
|
|
|
|
х − |
|
|
|
|
|
sin4 3x |
|
|
||||
1. |
lim |
|
, |
|
lim |
|
2 |
|
, |
3. |
lim |
|
|
|||||||||
|
|
|
|
|
|
|
|
(cos x −1)2 |
|
|||||||||||||
|
x2 |
− 8x +15 |
|
x − 4 |
|
|
|
|||||||||||||||
x→3 |
|
|
2. х→4 |
|
|
х→0 |
|
|
||||||||||||||
4. |
lim |
3tgx − 2tgx |
, |
|
5. |
lim |
|
x3 |
, |
|
6. |
lim |
ln(x +1) −ln x |
. |
||||||||
|
arcsin x |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
−4) −ln(x + 4) |
||||||||||||||
|
х→0 |
|
|
|
|
х→0 sin 3x |
|
|
|
|
x→∞ ln(x |
|
||||||||||

Самостоятельная работа №4 Вариант №17
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
th(x −1) |
|
|
|||||||||||
|
|
3 |
|
− 4 |
|
|
|
|
lim |
(x +1)100 −1 |
|
|
lim |
|
|
||||||||
1. |
lim |
x |
x |
|
, |
2. |
, |
3. |
|
||||||||||||||
|
|
x2 −1 |
|
|
1− x |
|
|||||||||||||||||
|
x→1 |
|
|
|
|
|
х→0 |
|
|
x |
|
|
|
х→1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
ax |
|
bx |
|
|
2 |
− 2x +3 |
x |
||||
|
|
(sin 5x) |
|
|
|
|
e |
|
− e |
|
|
|
|
x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4. |
lim |
|
|
x |
2 |
|
, |
5. |
lim |
|
|
x |
, |
6. |
lim |
2 |
−3x + 2 |
|
|||||
|
х→0 |
|
|
|
|
|
|
|
х→0 |
|
|
|
|
x→∞ |
x |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Самостоятельная работа №4 Вариант №18
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
x −sin x |
|
||||||||||||
|
|
x4 |
− 3x + 2 |
|
|
|
|
|
|
|
− 3 |
|
|
|
|||||||||||||
1. |
lim |
, |
|
2. |
lim |
1− x |
, |
3. |
lim |
||||||||||||||||||
|
|
|
x +sin 3x |
||||||||||||||||||||||||
x5 |
− 4х + 3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 + 3 |
|
|
x |
|||||||||||||||||||||||
|
x→0,5 |
|
|
|
х→1 |
|
|
|
|
х→0 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln(1+ e |
x |
) |
|
|
|
|
|
1 |
|
|
|||||
|
|
x arctg2x |
|
|
|
|
|
|
|
|
|
|
x2 |
|
|||||||||||||
|
lim |
|
|
|
lim |
|
|
|
|
lim(cos x) . |
|||||||||||||||||
4. |
|
|
|
|
|
, |
|
5. |
|
|
x |
|
, |
|
6. |
||||||||||||
|
arcsin |
2 |
x |
|
|
|
|
|
|||||||||||||||||||
|
х→0 |
|
|
|
|
|
х→−∞ |
|
|
|
|
|
|
|
|
x→0 |
|
|
|
||||||||
Самостоятельная работа №4 Вариант №19
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
4 |
|
|
− 2 |
|
|
|
|
|
|
lim(x + 3 |
|
|
|
). , |
|
|
|
|
|||||||||||||||||
|
lim |
x |
|
|
|
|
|
|
|
|
lim x sin 1 |
|||||||||||||||||||||||||||
1. |
|
|
|
, |
|
|
|
|
2. |
1− x3 |
|
3. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
x − 4 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x→16 |
|
|
|
|
|
|
|
|
|
х→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х→∞ |
|
|
|
x |
||||||||
|
lim 1− 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
sin 3x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
lim |
ln |
|
|
1+ x |
|
|
|
lim |
1 − chx |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
4. |
х→ |
π |
|
|
|
|
3x |
|
|
|
|
|
, |
5. |
x |
|
|
1− x , |
|
6. |
|
x . |
||||||||||||||||
6 |
|
tg |
|
−1 |
х→0 |
|
|
|
|
|
x→∞ |
|
||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №4 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №20 |
|
|
|
|
|
|
|
|
|
|||||||||||
Вычислить пределы функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x3 |
|
|
|||||
|
|
|
|
|
− |
|
|
х |
2 |
+ |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
||||||
1. |
lim |
1 |
|
|
1 , |
|
2. |
lim |
1 |
− |
х |
1 |
, |
3. |
lim |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
sin |
3 |
x |
||||||||||||||||
|
x→−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х→0 |
|
|
|
|
|
|
|
|
|
|
х→0 |
|
|||||||||
4. |
lim sin x −sin a , |
|
5. |
lim shx |
, |
|
|
|
|
|
6. |
lim lg(10x +1) . |
||||||||||||||||||||||||||
|
х→a |
|
|
|
x − a |
|
|
|
|
|
|
|
х→0 |
|
x |
|
|
|
|
|
|
|
|
x→∞ |
|
|
x |
|
|
|||||||||

Самостоятельная работа №4 Вариант №21
Вычислить пределы функций: |
|
|
|
lim cos x −cos a |
|||||||||||
|
|
3 |
|
− 4 |
|
|
, |
|
lim |
(x +1)1000 −1 |
|
|
|||
1. |
lim |
x |
x |
2. |
, |
3. |
|||||||||
|
|
|
|
|
|
||||||||||
|
x→1 |
|
x3 −1 |
|
х→0 |
x |
|
|
х→a |
x − a |
|||||
4. |
lim |
8sin2 x +1 |
|
lim chx −1 |
|
6. |
lim ln cos x |
||||||||
х→−π |
|
6x +π , |
|
5. х→0 |
x2 , |
|
x→0 |
x2 |
|||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №4 Вариант №22
Вычислить пределы функций:
1. |
lim |
x4 −120x − 25 |
, 2. |
lim |
|
9 − x |
− 3 |
. |
3. |
|||
x3 − 24х − 5 |
|
|
|
|
|
|||||||
2 |
− 3 x + 8 |
|||||||||||
|
x→5 |
|
х→0 |
|
|
|||||||
|
|
|
π |
|
|
|
|
||
|
|
sin x − |
6 |
|
|
lim thx |
|
||
|
lim |
|
|
|
|
|
|||
4. |
1− 4sin2 |
x , |
5. |
6. |
|||||
х→π |
х→0 x , |
||||||||
|
6 |
|
|
|
|
|
|
|
|
lim x −sin 2x
х→0 x +sin 5x
2
lim(cos2 x)x2 .
x→0
Самостоятельная работа №4 Вариант №23
Вычислить пределы функций:
|
3 |
|
x |
− 2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
πx |
|||||
|
|
|
|
|
|
|
1− x −1 |
|
|
|
|
|
||||||||||||||||
1. |
lim |
|
|
|
|
|
|
|
, |
|
2. |
lim |
|
, |
|
3. |
lim(1− x) tg |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2x − 4 |
|
|
|
|
|
2 |
|||||||||||||||||||||
|
x→8 |
|
|
|
|
х→0 |
|
|
|
|
2x |
|
|
|
|
|
х→1 |
|
||||||||||
|
lim cos5x |
− |
|
|
|
lim |
1 |
ln |
|
|
1 |
+ x 3 |
|
|
lim |
1 − shx . |
|
|||||||||||
4. |
x |
2cos 2x |
, |
5. |
x |
|
|
1 |
|
|
, |
6. |
|
|||||||||||||||
|
х→0 |
|
|
|
|
|
|
|
|
|
х→0 |
|
|
|
|
− x |
|
|
x→∞ |
x |
|
|||||||
Самостоятельная работа №4 Вариант №24
Вычислить пределы функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− x2 |
|
lim |
1 |
− |
|
х2 + |
1 |
|
|
lim |
10 |
1− х3 −1 |
, 3. |
lim |
|||||||||
1. |
|
|
|
x |
|
, |
2. |
|
|
|
|
|
|
|
|
|
sinπx |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
x |
||||||||||||||
|
x→0 |
|
|
|
|
|
|
|
х→0 |
|
|
|
|
х→1 |
||||||||
4. |
lim |
sin2 |
x −sin2 a |
, 5. |
lim |
sh3 x |
, |
|
|
|
|
6. |
lim ln(30x +1) . |
|||||||||
|
x |
2 |
− a |
2 |
|
|
x |
2 |
|
|
|
|
||||||||||
|
х→a |
|
|
|
|
|
|
х→0 |
|
|
|
|
|
|
|
|
x→∞ |
3x |
||||

Самостоятельная работа №4 Вариант №25
Вычислить пределы функций:
1. |
lim |
33 |
1+ x |
− 44 |
1+ x |
+1 |
, 2. |
lim |
(x +1)1000 −1 |
, |
|||
|
|
|
|
|
|
|
x +1 |
|
|||||
|
2 − 2 1+ x + х |
||||||||||||
|
x→0 |
|
|
х→−1 |
|
||||||||
4. |
lim |
8sin2 x − 2 |
5. |
lim ch2x −1 |
6. |
lim |
|
х→−π |
6x +π , |
х→0 |
x2 , |
x→0 |
|||
|
6 |
|
|
|
|
|
|
3. |
lim |
cos2 x −cos2 a |
|
x2 − a2 |
|||
|
х→a |
ln(ln x)
2x − 2e .
Самостоятельная работа №4 Вариант №26
Вычислить пределы функций:
|
|
x |
α |
− x |
β |
|
|
|
|
|
|
|
|
|
|
x |
2 |
− 2sin 2x |
||
|
lim |
|
lim |
|
9 − x − 3 |
|
. |
|
lim |
|||||||||||
|
|
|
|
|
|
|||||||||||||||
1. |
|
|
, 2. |
|
|
3. |
|
|||||||||||||
|
|
|
|
x |
2 |
+sin 5x |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
5 |
х −1 |
|
|
|||||||||||||||||
|
x→1 |
|
х→1 |
3 − 3 x + 28 |
|
х→0 |
|
|||||||||||||
|
|
|
π |
|
|
|
|
|
||
|
|
sin x − |
6 |
|
|
lim ln(thx +1) |
|
|||
|
lim |
|
|
|
|
|
||||
4. |
1− 4sin2 |
x , |
5. |
, |
||||||
х→π |
х→0 |
x |
||||||||
|
6 |
|
|
|
|
|
|
|
|
|
Самостоятельная работа №4 Вариант №27
Вычислить пределы функций:
2
6. limx (cos 2x)x2 .
→0
|
|
3 |
|
x |
− 2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πx |
|
|||
|
|
|
|
|
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1. |
lim |
|
|
|
|
|
|
, |
2. |
lim |
|
, |
|
3. |
lim(1 |
− x) tg |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2x |
− 4 |
2x − 2 |
|
|
2 |
|
||||||||||||||||||||||
|
x→+∞ |
|
|
х→1 |
|
|
|
х→1 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2cos5x −3cos 2x |
|
|
|
|
1 |
|
|
|
|
1+ x2 |
3 |
|
|
1 − shx |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
lim |
|
|
|
|
|
|
2 |
|
, |
5. lim |
|
|
2 ln |
|
2 |
6. |
lim |
|
|
. |
||||||||
|
|
|
|
|
x |
|
x |
|
1− x |
, |
|
x |
|||||||||||||||||
|
х→0 |
|
|
|
|
|
|
|
|
х→0 |
|
|
|
|
|
|
|
|
x→∞ |
|
|
||||||||
Самостоятельная работа №4 Вариант №28
Вычислить пределы функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
1− х2 +1 |
|
|
10 |
1− х3 −1 |
, |
|
lim |
||||||||
1. |
lim |
|
|
, |
2. |
lim |
|
|
|
|
|
|
3. |
|
|||
x2 |
|
|
|
|
|
|
sin2 πx |
||||||||||
x x |
|||||||||||||||||
|
x→0 |
|
|
х→0 |
|
|
х→0 |
||||||||||
|
|
х3 |
cos x |
−sin x |
|
|
|
sh3 x |
|
|
|
|
|
|
||
|
lim |
|
|
lim |
|
lim ln(30 |
x |
+1) . |
||||||||
4. |
|
|
|
, |
5. |
|
2 , |
6. |
||||||||
|
x |
5 |
x |
|||||||||||||
|
|
|||||||||||||||
|
х→0 |
|
|
|
|
|
х→0 |
|
|
x→∞ |
3 |
x |
||||

Самостоятельная работа №1
Вариант №1.
1. Исследовать функцию на экстремум:
z= 2xy −3x2 −2y 2 +10.
2.Исследовать функцию на условный экстремум:
z = 2x + 2y
при условии, что: y + x = 6.
Самостоятельная работа №1
Вариант №2.
1. Исследовать функцию на экстремум:
z= xy + x2 + y2 + х− у +1.
2.Исследовать функцию на условный экстремум:
z = 1x + 1y
при условии, что: x12 + y12 = а12 .
Самостоятельная работа №1
Вариант №3.
1. Исследовать функцию на экстремум:
z= 3xy + x2 + y2 + 2х+ у + 3.
2.Исследовать функцию на условный экстремум:
z = ху
при условии, что:
х2 + н2 = 2а2 .

Самостоятельная работа №1
Вариант №4.
1. Исследовать функцию на экстремум:
z= x2 y2 (6 + x + y).
2.Исследовать функцию на условный экстремум: z = 7x2 + y2 −12x + 4y
при условии, что:
y + x − 2 = 0
Самостоятельная работа №1
Вариант №5.
1. Исследовать функцию на экстремум:
z= 1x + 1y + 2x + 2y.
2.Исследовать функцию на условный экстремум:
z = x2 + y2
при условии, что:
ах + ву =1.
Самостоятельная работа №1
Вариант №6.
1. Исследовать функцию на экстремум:
z= 4xy − x2 − y2 − х− у + 3.
2.Исследовать функцию на условный экстремум:
z = 1x + 1y + х+ у
при условии, что:
1x + 1y = ху.

Самостоятельная работа №1
Вариант №7.
1. Исследовать функцию на экстремум:
z= 3xy + x2 + y2 + 2х+ у + 3.
2.Исследовать функцию на условный экстремум:
z = х2 у2
при условии, что:
х2 + у2 = 2а2 .
Самостоятельная работа №1
Вариант №8.
1. Исследовать функцию на экстремум:
z= х
 1+ у + y
1+ у + y
 1+ х.
1+ х.
2.Исследовать функцию на условный экстремум:
z = 6 −4x −3y
при условии, что:
х2 + у2 =1.
Самостоятельная работа №1
Вариант №9.
1. Исследовать функцию на экстремум:
z = 4xy + x4 + y4 − 2х2 − 2у2.
2. Исследовать функцию на условный экстремум:
z = ху
при условии, что:
х + у =1.
Самостоятельная работа №1
Вариант №10.
1. Исследовать функцию на экстремум:
z= xy + x2 + y2 − 2х− у + 3.
2.Исследовать функцию на условный экстремум:
z = х+ 2у
при условии, что:
х2 + у2 = 5.
Самостоятельная работа №1
Вариант №11.
1. Исследовать функцию на экстремум:
z= ху + 2x −3y.
2.Исследовать функцию на условный экстремум:
z = х4 + у4 − 36xy
при условии, что:
х2 + у2 =1.
Самостоятельная работа №1
Вариант №12.
1. Исследовать функцию на экстремум:
z= х4 + у4 − 36xy .
2.Исследовать функцию на условный экстремум:
z = ху
при условии, что:
х3 + у3 = 2ху.
Самостоятельная работа №1
Вариант №13.
1. Исследовать функцию на экстремум:
z= y4 + x2 − 2хy2 − у5.
2.Исследовать функцию на условный экстремум:
z = ху
при условии, что:
х2 + у2 = 8.
Самостоятельная работа №1
Вариант №14.
1. Исследовать функцию на экстремум: u = ху + zx + yz.
2. Исследовать функцию на условный экстремум:
z = х3 + у3
при условии, что:
х+ у = 2.
Самостоятельная работа №1
Вариант №15.
1. Исследовать функцию на экстремум: u = х+ у + z − x2 − y2 − z2 ..
2. Исследовать функцию на условный экстремум:
z = ху
при условии, что:
х3 + у3 = ху4 .
Самостоятельная работа №1
Вариант №16.
1. Исследовать функцию на экстремум:
z= y4 + x2 − 2хy2 − у3.
2.Исследовать функцию на условный экстремум:
z = х2 у2
при условии, что:
х2 + у2 = 2ху.
Самостоятельная работа №1
Вариант №17.
1. Исследовать функцию на экстремум:
u= 2ху − zx + 2yz.
2.Исследовать функцию на условный экстремум:
z = х3 + у3
при условии, что:
3х+ у = 2.
Самостоятельная работа №1
Вариант №18.
1. Исследовать функцию на экстремум:
u= хуz − x2 − y2 − z2 ..
2.Исследовать функцию на условный экстремум:
z = х2 у2
при условии, что:
х+ у = ху.
Самостоятельная работа №1
Вариант №19.
1. Исследовать функцию на экстремум:
z= y2 + x2 − 2хy − у3 + х3.
2.Исследовать функцию на условный экстремум:
z = х2 у2
при условии, что:
3х2 + 2у2 = ху.
Самостоятельная работа №1
Вариант №20.
1. Исследовать функцию на экстремум:
u= 2ху − 4zx + yz.
2.Исследовать функцию на условный экстремум:
z = х3 + у3 − ху
при условии, что:
3х+ у = 2.
Самостоятельная работа №1
Вариант №21.
1. Исследовать функцию на экстремум:
u= хуz + x2 + y2 + z2 ..
2.Исследовать функцию на условный экстремум:
z = х2 + у2
при условии, что:
х+ у = ху.
Самостоятельная работа №1
Вариант №22.
1. Исследовать функцию на экстремум:
z = y2 + x2 + хy − 2у3 + х3.
2. Исследовать функцию на условный экстремум:
z = ху
при условии, что:
х2 + у2 = ху.
Самостоятельная работа №1
Вариант №23.
1. Исследовать функцию на экстремум:
u= 2ху − 4zx + yz.
2.Исследовать функцию на условный экстремум:
z = х3 + у3 − ху
при условии, что:
х+ у =1.
Самостоятельная работа №1
Вариант №24.
1. Исследовать функцию на экстремум:
u= хуz + x2 + y2 + z2 .
2.Исследовать функцию на условный экстремум:
z = х2 + у2
при условии, что:
х+ у = ху.

Самостоятельная работа №1
Вариант №25.
1. Исследовать функцию на экстремум:
z= y2 − x2 − 2хy−3у3 + х3.
2.Исследовать функцию на условный экстремум:
z = х3 у2
при условии, что:
3х3 + 2у2 = х2 у.
Самостоятельная работа №1
Вариант №26.
1. Исследовать функцию на экстремум:
u= 2ху− 4zx + 
 yz.
yz.
2.Исследовать функцию на условный экстремум:
z = х3 + у3 − ху
при условии, что:
х+ у = 2.
Самостоятельная работа №1
Вариант №27.
1. Исследовать функцию на экстремум:
u= −хуz + x2 + y2 + z2 .
2.Исследовать функцию на условный экстремум:
z = х2 + у2
при условии, что:
х+ у =1у.

Вариант №22
Исследовать функцию на условный экстремум.
z = 1x − 1y + x + y
при условии, что: y - x = 6
Решение: Cоставим функцию Лагранжа
ψ = |
1 + |
|
1 |
|
|
+ x + y +λy −λx −6λ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Исследуем её на условный экстремум. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂ψ |
= 0; |
|
|
|
|
|
∂ψ |
|
= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∂ψ |
|
= − |
1 |
|
|
|
+1− |
λ; |
∂ψ |
|
= − |
1 |
|
|
+1+λ; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
∂x |
|
|
|
|
x2 |
∂y |
y 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
=1− |
|
λ, |
|
|
|
|
x = ± |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
=1+ |
|
λ, |
|
y = ± |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y − x |
1+λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
y − x = 6; |
|
|
|
|
|
|
|
|
|
= 6; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
I) ( |
|
1 |
|
|
|
|
|
; |
|
|
|
|
1 |
|
|
); |
|
( − |
1 |
|
|
|
|
|
|
|
;− |
|
1 |
|
|
): |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
1− λ |
|
|
|
|
1+ λ |
|
|
|
|
1− λ |
1+ λ |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
D(f): 1- λ ≥ 0; 1+λ ≥ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
λ |
|
≤ 1; |
|
|
λ ≥ -1;значит ; |
|
| λ| ≤ 1; |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
− |
|
|
|
1 |
|
|
|
|
|
= 6; |
|
|
|
|
|
|
|
|
|
|
− |
|
1 |
|
|
|
+ |
|
1 |
|
= 6; |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1−λ |
|
|
|
|
|
|
|
|
1+λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−λ |
|
1+λ |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
0 < λ <1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 < λ < 0; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
= 6 1−λ2 ; |
|
|
|
|
|
− |
|
= 6 1−λ2 ; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1+λ |
1−λ |
|
|
|
|
1−λ |
1+λ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1+λ +1−λ −2
 1−λ2 = 36(1−λ2 ); 2 −2
1−λ2 = 36(1−λ2 ); 2 −2
 1−λ2 = 36(1−λ2 ); 1−
1−λ2 = 36(1−λ2 ); 1− 
 1−λ2 =18(1−λ2 );
1−λ2 =18(1−λ2 );
Произведём замену переменной: ; 
 1−λ2 = t ≥ 0.
1−λ2 = t ≥ 0.
18t2 + t −1 = 0; |
|
|
|
|
|
|
||
|
= −1+ |
|
|
|
|
= −1− |
|
|
t |
1+ 72 |
> 0 |
t |
2 |
73 |
< 0; |
||
1 |
36 |
|
|
36 |
|
|
||
|
|
|
|
|
|
|||
t2 - посторонний корень т.к.t ≥ 0;
1−λ2 = 
 73 −1; 36
73 −1; 36
|
|
|
|
|
|
|
|
|
|
|
362 −( |
|
|
−1)2 |
|
|
|
|
|
|
|
|
|
|
= ± |
1222 −2 |
|
|
≈ ±0,96 D( f ) |
|||
λ = ± |
73 |
73 |
||||||||
1,2 |
36 |
2 |
|
|
36 |
|
|
|
||
|
|
|
|
|
|
|||||
1) λ = 
 1222 −2
1222 −2
 73 ; 36
73 ; 36
для точки M1:
x = |
|
6 |
|
|
|
|
≈ 5,29; y = |
|
6 |
|
|
|
|
≈ 0,71; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
36 + |
|
|
|
|
|||||||
36 − 1222 − 2 |
|
|
362 −( |
|
−1)2 |
|||||||||||
|
|
73 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
73 |
|
|
|
||||||
Посторонние корни т. к. y - x = 0,71 – 5,29 = -4,58≠6
для точки M2:
x = − |
|
|
6 |
|
|
|
|
≈ −5,29; y = − |
|
6 |
|
|
|
|
≈ −0,71; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
36 − |
1222 −2 |
|
|
|
|
|
|
36 + 1222 −2 |
|
|
|
|
|
|
73 |
|
|
|
|
|
73 |
|
|
|
|
||||||
Посторонние корни т. к. y - x = -0,71 +5,29 = 4,58≠6;

2) λ = − 
 1222 −2
1222 −2
 73 36
73 36
для точки M3:
x = |
|
6 |
|
|
|
|
≈ 0,71; y = |
|
|
6 |
|
|
|
|
≈ 5,29; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
36 + 1222 −2 |
|
|
|
|
|
|
36 − |
1222 −2 |
|
|
|
|
|
|
|
|
73 |
|
|
|
73 |
|
|
|
|
||||||
Посторонние корни т. к. y - x = 5,29-0,71 = 4,58≠6; для точки M4:
x = − |
|
6 |
|
|
|
|
≈ −0.71; y = − |
|
|
6 |
|
|
|
|
≈ −5,29; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
36 + 1222 −2 |
|
|
|
|
|
|
36 − |
1222 −2 |
|
|
|
|
|
|
|
|
73 |
73 |
|
|
|
|
|||||||||
|
|
|
|
|
Посторонние корни т. к. |
|
y - x = – 5,29+0,71 = -4,58≠6 |
|||||||||||||||||||||||||||||||||||||||||
II) ( − |
|
1 |
|
|
|
; |
|
1 |
|
|
|
|
); ( |
1 |
|
|
;− |
|
1 |
|
|
|
): |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1− λ |
|
1+ |
|
λ |
|
1− λ |
|
|
1+ λ |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
D(f): 1- λ ≥ 0; 1+λ ≥ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
λ ≤ 1; λ ≥ -1; значит; |
| λ| ≤ 1; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
+ |
|
|
|
|
1 |
|
= 6; |
|
|
|
− |
|
|
|
|
|
1 |
|
|
|
|
|
− |
|
1 |
|
= 6; |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1+ λ |
|
1−λ |
|
|
|
1+ λ |
|
|
1−λ |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
+ |
|
|
|
|
|
|
|
= 6 1−λ2 ; |
|
|
|
+ |
|
= −6 1−λ2 ; |
||||||||||||||||||||||||||||||
1−λ |
1+ λ |
|
1−λ |
1+ λ |
||||||||||||||||||||||||||||||||||||||||||||
1−λ +1+ λ + 2
 1−λ2 = 36(1−λ2 ); 2 + 2
1−λ2 = 36(1−λ2 ); 2 + 2
 1−λ2 = 36(1−λ2 ); 1+
1−λ2 = 36(1−λ2 ); 1+ 
 1−λ2 =18(1−λ2 );
1−λ2 =18(1−λ2 );
Произведём замену переменной: 
 1− λ2 = t, t ≥ 0;
1− λ2 = t, t ≥ 0;
18t 2 |
−t −1 = 0; |
|
|
|
|
|
|
|
1+ |
|
|
|
1− |
|
|
t1 = |
1+72 |
> 0 t2 |
= |
73 |
< 0; |
||
|
36 |
|
|
36 |
|
||
t2 - посторонний корень т.к.t ≥ 0;

|
|
|
|
|
1+ |
|
73 |
|
|
|
|
|
|
|
|
1−λ2 |
= |
; |
|
|
|
|
|
||||||
|
|
|
|
|
36 |
|
|
|
|
|
|
|
||
|
|
|
|
|
362 |
−( |
|
|
+1)2 |
|
||||
λ |
= ± |
|
|
|
73 |
≈ ±0,96 D( f ) |
||||||||
1,2 |
|
|
|
|
362 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
|
1222 + 2 |
|
|
|
; |
|
|||||||
1) λ = |
73 |
|
||||||||||||
|
|
|
|
|
|
362 |
|
|
|
|
|
|
|
|
для точки M5:
x = − |
|
|
6 |
|
|
|
|
≈ −5,29; y = |
|
6 |
|
|
|
|
≈ 0,71; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
36 − |
1222 + 2 |
|
|
|
|
|
|
36 + 1222 + 2 |
|
|
|
|
|
||
73 |
|
|
|
|
|
73 |
|
|
|
|
|||||||
y - x = 0,71 + 5,29 = 6,00 ≈6;
|
∂2ψ |
∂2ψ |
|
2 |
0 |
|
−0,0135 |
0 |
|
|||
|
|
|
|
|||||||||
∆ = |
∂x2 |
∂x∂y |
= |
x3 |
= |
= −0,0755 < 0, |
||||||
2 |
||||||||||||
|
∂2ψ |
∂2ψ |
|
0 |
|
0 |
5,59 |
|
||||
|
|
|
|
|
|
y3 |
|
|
|
|
||
|
∂y∂x |
∂y 2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
значит точка М5 не является точкой экстремума функции. для точки M6:
x = |
|
6 |
|
|
|
|
≈ 5,29; y = − |
|
|
6 |
|
|
|
|
≈ −0,71; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
36 − 1222 + 2 |
|
36 + |
1222 + 2 |
|
|
|
|
|
|||||||
|
|
73 |
73 |
|
|
|
|
||||||||||
Посторонние корни т. к. y - x = -0,71 -5,29 = -6,00≠6;
2) λ = − 1222 + 2 |
73 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
362 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
для точки M7: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x = − |
|
|
6 |
|
|
|
|
≈ −0,71; y = |
|
6 |
|
|
|
|
≈ 5,29; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
36 + |
1222 + 2 |
|
|
|
|
|
|
36 − 1222 + 2 |
|
|
|
|
|
|||||
73 |
|
|
|
|
|
73 |
|
|
|
|
||||||||

y - x = 5,29+0,71 = 6,00 ≈ 6;
∂2ψ
∆= ∂x2
∂2ψ
∂y∂x
∂2ψ |
|
2 |
0 |
|
−5,59 |
0 |
|
||
|
|
|
|||||||
∂x∂y |
= |
x3 |
= |
= −0,0755 < 0, |
|||||
2 |
|||||||||
∂2ψ |
|
0 |
|
0 |
0,0135 |
|
|||
∂y 2 |
|
|
y3 |
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
значит точка М7 не является точкой экстремума функции. для точки M8:
x = |
|
6 |
|
|
|
|
≈ 0.71; y = − |
|
6 |
|
|
|
|
≈ −5,29; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
36 − |
|
|
|
|
|||||
|
36 + |
362 −( |
|
+1)2 |
|
|
362 −( |
|
+1)2 |
|||||||
|
|
73 |
|
|
|
|
73 |
|
|
|
||||||
Посторонние корни т. к. y - x = 0,71 – 5,29 = -4,58≠6
Ответ: Функция не содержит точек экстремума.
Вариант №12.
Исследовать функцию на условный экстремум.
z = 7x2 + y2 −12x + 4y
при условии:
y + x − 2 = 0
Решение:
Составим функцию Лагранжа:
ψ = 7x 2 + y 2 −12x + 4y +λy +λx −2λ
Исследуем её на условный экстремум:

∂ψ |
= 0; |
∂ψ = 0; |
|
|
|
|
|
|
|
|
|
|
|||
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
||
∂ψ |
= 14x −12 |
+ λ; |
∂ψ |
|
= 2 y + |
4 + λ; |
|
||||||||
∂x |
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
∂2ψ = 14; ∂2ψ |
= 2; |
∂2ψ |
= 0; |
∂2ψ |
|
= |
0; |
||||||||
∂x∂y |
∂y∂x |
||||||||||||||
∂x2 |
|
∂y 2 |
|
|
|
|
|||||||||
x = |
12 − λ ; y = − 4 + λ |
; |
|
|
|
|
|
|
|
||||||
|
14 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
12 − λ − |
λ + 4 |
− 2 = 0; |
|
|
|
|
|
|
|
|
|
||||
14 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
12 − λ − 7λ − 28 −14 = 0; |
|
|
|
|
|
||||||||||
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
− 8λ − 30 = 0; λ = − 30 |
8 |
= −15 |
4 |
; |
|
|
|
||||||||
|
12 +15 4 |
|
|
|
|
|
|
|
|
|
|||||
x = |
= |
63 ; y = |
15 −16 |
= − |
1 |
; |
|||||||||
14 |
|
8 |
|
8 |
|||||||||||
|
|
56 |
|
|
|
|
|
|
|
|
|||||
Составим определитель:
∂2ψ |
∂2ψ |
|
14 |
0 |
|
|
∂x2 |
∂x∂y |
= |
= 28 > 0 , значит точка М(63/56;-1/8) является точкой |
|||
2 |
|
2 |
|
0 |
2 |
|
∂ ψ |
∂ ψ |
|
|
|||
∂y∂x |
|
∂y2 |
|
|
|
|
экстремума,
т.к.∂2ψ (63 / 56;−1/ 8) > 0, то точка М(63/56;-1/8) является точкой минимума
∂x2
Ответ: М(63/56;-1/8) - точка минимума.
Вариант №22
Найти экстремум функции:
z = x2 y2 (6 + x + y);
Решение:
z = 6x2 y2 + x3 y2 + x2 y3 ; |
|
|
|
|
|
|
|
|
|
||||||||||||
∂z =12xy2 + 3x2 y2 + 2xy3 ; |
|
∂z |
=12x2 y + 3x2 y2 + 2x3 y; |
||||||||||||||||||
|
∂y |
||||||||||||||||||||
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 z |
=12y2 + 6xy2 + 2y3 ; |
|
|
∂2 z |
=12x2 + 6x2 y + 2x3 ; |
||||||||||||||||
∂x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y2 |
|
|
|
|
|
|
∂2 z |
|
= |
∂2 z |
|
|
= 24xy + 6x |
2 |
y |
+ 6xy |
2 |
|
|
|
||||||||
∂x∂y |
∂y∂x |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
2 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
2 |
(12 + 3x + 2y)= 0, |
||
12xy |
|
+ 3x |
|
|
y |
|
+ 2xy |
|
= |
|
0, |
|
xy |
|
|||||||
12x2 y |
+ 3x2 y2 + 2x3 y = 0; |
|
|
|
yx2 |
(12 + 3y + 2x)= 0; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим три случая: |
|
|
|
|
|
|
|
|
|
|
|
1) x = ξ , (причём ξ→0; ξ ≠ 0); y Є R: |
|
∆ = |
|
2y2 + 2y3 |
0 |
|
= 0 |
||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
0 |
0 |
|
|
2) x Є R; y = 0: |
∆ = |
|
0 |
0 |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
2x2 + 2x3 |
|
|
|
|
|
|
|
На осях нет точек экстремума.
3)12 + 3x + 2y = 0,12 + 3y + 2x = 0;
Сложив, получим:
3(x − y)+ 2(y − x)= 0
(x − y)(3 − 2)= 0
x = y,
значит 12+5x = 0
x = − |
12 |
; |
y = − |
|
12 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 z |
= |
123 |
− |
6 |
12 |
3 |
|
2 |
123 |
= − |
123 |
×3 |
; |
|
|
|
|
|
|
||||||||||
∂x2 |
|
52 |
53 |
− |
|
53 |
53 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∂2 z |
= − |
3*123 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∂y2 |
|
53 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∂2 z |
|
|
|
|
|
|
∂ |
2 z |
|
|
123 |
|
|
123 |
|
123 |
|
×2 |
|
|
1 |
|
2 ×12 |
3 |
|||||
|
|
|
= |
|
|
|
|
= 2 |
|
|
|
− |
|
= |
|
|
|
|
1 |
− |
|
|
= − |
|
; |
||||
∂x∂y |
|
∂y∂x |
|
52 |
|
53 |
|
5 |
2 |
6 |
53 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
M(-12/5;-12/5)-исследуемая точка.

|
− |
3×123 |
− |
2×123 |
|
|
123 |
|
3 |
2 |
|
12 |
|
3 |
|
∆ = |
125 |
125 |
|
= |
|
|
|||||||||
|
|
|
125 |
|
2 |
3 |
|
= 5 |
5 |
|
> 0, значит точка М-точка |
||||
|
− |
2×123 |
− |
3×123 |
|
|
|
|
|
|
|
||||
|
125 |
125 |
|
|
|
|
|
|
|
|
|
|
|
||
экстремума функции.
∂2 z < 0, то точка М-точка максимума функции.
∂x2
Ответ: М(-12/5;-12/5)-точка максимума функции.
Вариант №20
Найти экстремум функции:
z = 1x + 1y + 2x + 2y;
Решение: Необходимые условия:
∂∂xz = 0; ∂∂yz = 0
∂z = − |
1 |
|
+ 2; |
|
|
|
∂z |
|
= − |
1 |
+ 2; |
|
|
|
|
|
|
|
|||||||||||||||
x 2 |
|
|
|
∂y |
|
y 2 |
|
|
|
|
|
|
|
||||||||||||||||||||
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∂2 z |
= |
|
|
2 |
; |
|
|
∂2 z |
|
= |
|
2 |
|
; |
|
|
|
|
|
|
|
|
|||||||||||
∂x 2 |
|
|
x 3 |
|
|
∂y 2 |
|
|
y 3 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∂2 z |
|
= |
|
∂2 z |
|
= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∂x∂y |
|
∂y∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∂z |
|
|
|
|
|
|
− |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
= |
0; |
|
+ |
|
2 = 0, |
|
|
|
x1,2 |
= ± |
|
|
|
|
, |
||||||||||||||||||
|
∂x |
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∂z |
|
|
0; |
|
|
1 |
|
|
|
|
2 |
= 0; |
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
|
= |
− |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∂y |
|
|
|
|
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
y1,2 |
= ± |
2 |
|
; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) M1 |
|
1 |
|
|
1 |
|
|
|
|||
|
|
|
; |
|
|
: |
|||||
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
∂2 z |
|
|||
|
|
|
|
|
|
|
|
||||
|
∆ |
1 |
= |
∂x 2 |
|
||||||
|
|
|
|
|
|
∂2 z |
|
||||
|
|
|
|
|
|
|
∂y∂x |
|
|||
2) M2 |
|
|
|
1 |
|
1 |
|
|
|
||
|
− |
|
|
; |
|
|
|
|
: |
||
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
∂2 z |
|
|
|||
|
|
|
|
|
|
|
|
||||
|
∆ |
2 |
= |
∂x2 |
|
|
|||||
|
|
|
|
|
∂2 z |
|
|
||||
|
|
|
|
|
|
∂y∂x |
|
|
|||
∂2 z
∂x∂y ∂2 z
∂y 2
∂2 z
∂x∂y ∂2 z
∂y 2
= |
4 |
2 |
0 |
|
= 32, значит точка М1-точка минимума. |
|
0 |
4 |
2 |
|
|
= |
−4 |
2 |
0 |
|
= −32, значит точка М2. не является точкой |
|
0 |
|
4 |
2 |
|
экстремума.
3) M3 |
|
1 |
|
|
|
1 |
|
|
|
|
|||
|
|
|
;− |
|
|
|
: |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
∂2 z |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
∆ |
3 |
= |
∂x2 |
|
|
|||||||
|
|
|
|
|
|
∂2 z |
|
|
|||||
|
|
|
|
|
|
|
∂y∂x |
|
|
||||
∂2 z
∂x∂y ∂2 z
∂y 2
= |
4 |
2 |
0 |
|
= −32, значит точка М3 не является точкой |
|
0 |
−4 |
2 |
|
|
экстремума.
4) M4 |
|
|
1 |
|
|
1 |
|
|
|
||
|
− |
|
|
|
;− |
|
|
|
|
: |
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
∂2 z |
∆ |
4 |
= |
∂x2 |
|
|
∂2 z |
|
|
|
|
∂y∂x |
Ответ:
∂2 z
∂x∂y ∂2 z
∂y 2
= |
−4 |
2 |
0 |
|
= 32, значит точка М4-точка максимума. |
|
0 |
|
−4 |
2 |
|

точка максимума: M4 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|||||
|
− |
|
|
|
|
;− |
|
|
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
точки минимума: M1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
; |
|
|
|
|
|
|
|
; |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

§ 4. Условный экстремум
I. Понятие условного экстремума. В § 6 гл. 13 мы занимались отысканием локальных экстремумов функции, аргументы которой не связаны никакими дополнительными условиями. Вместе с тем в математике и в ее приложениях часто встречается задача об отыскании экстремумов функции, аргументы которой удовлетворяют дополнительным условиям связи. Экстремумы такого рода мы будем называть условными, чтобы отличить их от (безусловных) экстремумов, изученных в § 6 гл. 13. Приведем пример задачи об отыскании условного экстремума. Пусть требуется найти экстремум функции и = х2 + г/2 при условии, что аргументы этой функции удовлетворяют условию связи
х + У—1=0. Таким образом, экстремумы функции и = х2 + уг ищутся не на
Рис. 14.6.
всей плоскости Оху, а лишь на прямой х +у—1=0. Для решения поставленной задачи
подставим в выражение функции и = х2+у2 значение у, определяемое из условия связи х + у—1 =0. Таким путем мы сведем поставленную задачу к задаче об отыскании безусловного экстремума функции и = 2х2 — 2х+ 1.
Последний экстремум находится без труда: поскольку и '=4(х—1/2), и(2) = 4, то функция и
=2х2—2х+1 имеет минимум и =1/2 при х =1/2. Таким образом, функция и = х2 + уг с
условием связи х+у—1=0 имеет условный минимум и =1/2 в точке (1/2, 1/2). Отметим, что безусловный минимум функции и = х2+у2 достигается в точке (0, 0) и равен и = 0. Впрочем, даже из наглядных соображений (рис. 14.6) очевидно, что минимум функции и
=х2+у2 (графиком которой служит параболоид вращения) на всей плоскости Оху не совпадает с ее минимумом на прямой х + у—1=0.
Переходим к общей постановке задачи об отыскании условного экстремума. Пусть требуется найти экстремум функции т+п переменных
и=f(х1,…, хn, у1,…, уm )
(14.40)
при наличии т условий связи
F1 |
(x1, |
..., хп, у1,…, уm )=0 |
|
|
|
|
|
F2 |
(x1,..., |
хп, |
у1,…, |
уm |
)=0 |
} |
|
(14.41) |
|
|
|
|
|
||
………………………… |
|
|
|
|
|||
Fm(x1 |
,..., хп, y1,..., уm ) =0 |
|
|
|
|
||
Прежде всего уточним само понятие условного экстремума функции (14.40) при наличии связей (14.41). Будем говорить, что функция (14.40) при наличии связей (14.41) имеет условный максимум (минимум) в точке М0(х01, ..... х0п, у01, ..., y0m). координаты которой удовлетворяют условиям связи (14.41), если найдется такая окрестность точки Мо, в пределах которой значение функции (14.40) в точке Мо является наибольшим (наименьшим) среди ее значений во всех точках, координаты которых удовлетворяют условиям связи (14.41).
Для нахождения условного экстремума функции (14.40) при наличии связей (14.41) предположим, что функции, стоящие в левых частях равенств (14.41), дифференцируемы
1
в некоторой окрестности рассматриваемой точки Мо, причем в самой точке Мо частные производные указанных функций по y1, ..., ут непрерывны, а якобиан
D ( F1, …, Fm )/D( y1,..., уm ) |
(14.42) |
отличен от нуля.
В таком случае в силу теоремы 14.2 для достаточно малых положительных чисел ех, е2,
..., eт найдется такая окрестность точки М'0(х01,..., х0n) пространства переменных (х1,..., хп), что всюду в пределах этой окрестности определены т функций
y1=φ1(x1,…,xn), |
|
y2=φ2(x1,…,xn), } |
(14.43) |
……………….
ym=φm(x1,…,xn),
удовлетворяющих условиям |у1—у1|<e1, ..., |уm—уm|<еm и являющихся при наличии этих условий единственным и дифференцируемым решением системы уравнений (14.41). Подставляя найденные функции (14.43) в (14.40), мы сведем вопрос о существовании условного экстремума в точке Мо у функции (14.40) при наличии связей (14.41) к вопросу о существовании безусловного экстремума в точке М'о у сложной функции аргументов
x1,x 2,…, xn,
u=f[x1,…,xn, φ1(x1,… xn),…, φm(x1,…,xn)]= Φ(x1,…,xn). (14.44)
Вопрос о существовании безусловного экстремума функции (14.44) может быть решен методами, указанными в § 6 гл. 13 *). Изложенная нами общая схема сведения условного экстремума к безусловному была реализована в рассмотренном выше частном примере. Постараемся теперь, не прибегая к решению системы (14.41), установить по крайней мере необходимые условия существования условного экстремума в точке Мо. Итак, пусть функция (14.40) дифференцируема в точке Мо и имеет в этой точке условный экстремум при наличии связей (14.41) или (что то же самое) функция (14.44) имеет в точке М'й безусловный экстремум. Согласно установленному в § 6 гл. 13 необходимым условием безусловного экстремума функции м = Ф(x 1( ;.., х„) в точке М'о является равенство нулю в этой точке дифференциала этой функции
du=(dΦ/d x1)dx1+…+(dF/dxn)dxn, (14.45)
тождественное относительно dx1, ..., dxn. В силу инвариантности формы первого дифференциала и равенства (14.44) формулу (14.45) можно переписать в виде
du = (df/dx1)dx1 +…+ (df/dxn)dxn + (df/dy1)dy1 +…+ (df/dym)dym = 0 (14.46)
(В этой формуле все частные производные берутся в точке Мо.) Подчеркнем, однако, что в равенстве (14.46) dy1, ...,dym представляют собой дифференциалы функций (14.43), так что равенство (14.46) не является тождеством относительно dy1, ..., dym. Предположим, что в уравнения связи (14.41) мы подставили функции (14.43), являющиеся решением системы (14.41). При этом уравнения (14.41) обратятся в тождества, и мы получим, дифференцируя эти тождества,
(dF1/dx1)dx1 +…+ (dF1/dxn)dxn + (dF1/dy1)dy1 +…+ (dF1/dym)dym = 0,
………………………………………………………………… |
} (14.47) |
(dFm/dx1)dx1 +…+ (dFm/dxn)dxn + (dFm/dy1)dy1 +…+ (dFm/dym)dym = 0
Так как якобиан (14.42), по предположению, отличен от нуля в точке Мо, то из линейной системы (14.47) dy1, . . ., dym могут быть выражены как линейные функции dx1 ..., dxn. Если найти эти выражения и подставить их в (14.46), то, собирая в полученном равенстве члены, содержащие dx1, ..., dxn, мы будем иметь
A1* dx1+…+An * dxn=0, (14.48)
где через А1, ...,Ап обозначены некоторые рациональные функции частных производных f, F1, ..., Fm в точке Мо. Так как в равенстве (14.48) фигурируют лишь дифференциалы
независимых переменных, то из этого равенства заключаем, что А1 = 0, . .., A n= 0. Присоединяя к указанным равенствам m условий связи (14.41), мы получим необходимые
2
условия существования условного экстремума функции (14.40) при наличии связей (14.41) в виде
A1=0, ..., Аn = 0, F1 =0,…, Fm=0. (14.49)
Равенства (14.49) представляют собой систему т+п уравнений для определения т+п координат точки возможного экстремума.
2. Метод неопределенных множителей Лагранжа. При изложенном выше методе отыскания точек возможного условного экстремума мы нарушили симметрию в отношении переменных х1, ..., хп, у1, ..., ут. Часть из этих переменных х1, ..., хn мы рассматривали как независимые, остальные — как функции | этих переменных. В ряде случаев это приводит к усложнению | выкладок. Лагранжем предложен метод, симметризирующий роль I переменных. Изложению этого метода и посвящен настоящий пункт. Умножим равенства (14.47) соответственно на произвольные (и пока еще
неопределенные) постоянные множители λ1…,λт. Полученные после умножения равенства сложим почленно с равенством (14.46). В результате получим следующее равенство:
(dψ/dx1)dx1+…+(dψ/dx1)dxn + (dψ/dy1)dy1+…+ (dψ/dym)dym=0 (14.50)
где символом ψ(x1,..., xn , y1,..., ym) обозначена следующая функция:
ψ = f +λ1F1+…+λ mF m. (14.51)
Эту функцию мы в дальнейшем будем называть функцией Лагранжа. Считая, что для функций (14.41) выполнены условия, сформулированные в предыдущем пункте, и что
функция (14.40) дифференцируема, выберем множители λ1,…,λ m так, чтобы выполнялись равенства
dψ/dy1=0 dψ/dym=0
Это заведомо можно сделать, ибо равенства (14.52) приводят к линейной системе
df/dy1 + λ1(dF1/ dy1)+…+ λm(dFm/dy1)=0 {…………………………………………….
df/dym+ λ1(dF1/ dym) +…+ λm(dFm/dym)=0
определитель которой (якобиан (14.42)) отличен от нуля. В силу равенств (14.52) равенство (14.50) принимает вид
(dψ/dx1)dx1+…+( dψ/dxn)dxn=0 |
(14.53) |
Поскольку при сделанных выше предположениях переменные х1 ..., хп являются независимыми, то из равенства (14.53) заключаем, что
dψ/dx1=0,…, dψ/dxn=0
Присоединяя к уравнениям (14.52) и (14.54) условия связи (14.41), мы получим систему п + 2т уравнений
dψ/dx1=0,…, dψ/dxn=0 dψ/dy1=0,…, dψ/dym=0 (14.55)
F1=0,…, Fm=0,
для определения п+т координат точек возможного условного экстремума и т
множителей λ1? . .., λт. Практически при реализации этого метода поступают следующим образом. Составляют функцию Лагранжа (14.51) и для этой функции находят точки
возможного безусловного экстремума. Для исключения множителей λ1, ..., λт привлекают условия связи (14.41). Такой путь отыскания точек возможного условного экстремума является законным, ибо он приводит нас как раз к системе п+2т уравнений (14.55). Пример применения метода множителей Лагранжа будет рассмотрен в п. 4.
3. Достаточные условия. В этом пункте мы рассмотрим один из путей дополнительного исследования точек возможного условного экстремума. Предположим, что в точке Мо выполнены необходимые условия экстремума (14.55). Кроме того, дополнительно потребуем двукратной дифференцируемости функций (14.40) и (14.41) в окрестности точки Мо и непрерывности всех частных производных второго порядка в
3
самой точке Мо. Из конструкции функции Лагранжа (14.51) очевидно, что при наличии связей (14.41) экстремумы функций (14.40) и Лагранжа совпадают*). Но тогда из результатов § 6 гл. 13 вытекает, что для получения достаточного условия экстремума в точке Мо у функции (14.40) при наличии связей (14.41) следует присоединить к условиям
(14.55) требование знакоопределенности в этой точке d2ψ. При этом в соответствии с результатами § 6 гл. 13 мы можем констатировать наличие в точке Мо минимума, если
при наличии связей (14.41) d2ψ]M0 > 0, и максимума, если d2ψ] Mo<0. Сделаем еще несколько замечаний практического характера. Прежде всего отметим, что второй
дифференциал d2ψ можно в данной точке Мо возможного экстремума вычислять так, как если бы
все переменные х1,…xn,y1,…,ym были независимыми. В самом
деле, в общем случае второй дифференциал d2ψ функции Ψ не обладает свойством инвариантности формы и должен был бы с учетом зависимости y1 ..., ут от x1 ..., хп определяться равенством
d2ψ =(dx1(d/d x1)+…+ dxn(d/d xn)+ dy1(d/d y1)+…+ dym(d/d
ym))2Ψ+(dΨ/dy1)d2y1+…+(dΨ/dym)d2ym. Но в точке возможного экстремума Мо справедливы равенства dΨ/dy1=0 ,…, dΨ/dym =0
так что d2Ψ определяется той же формулой
той же формулой d2ψ =(dx1(d/d x1)+…+ dxn(d/d xn)+ dy1(d/d y1)+…+ dym(d/d ym))2Ψ.
(14.56).
что и в случае, когда все переменные x1,…,xn y1,…,ym независимы. Далее, заметим что поскольку нам требуется установить знакоопределённость d2Ψ лишь при наличае связи
(14.41), то при проведении вычислений следует в формулу (14.56) для d2ψ подставить в место dy1 ,…,dym их значения, определяемые из системы (14,47). После этого следует
изучить вопрос о знакоопределенности d2Ψ данной точке Мо .
4. Пример. Найдем экстремальные значения функции m Переменных
u=x21 + x22 +…+ x2m |
(14.57) |
при наличии связи |
|
x1+x2+…+xm+1=0 |
(14.58) |
Составим функцию Лагранжа
Ψ=x21+…+x2m+λ(x1+…+xm-1) (14.59)
И для неё изучим вопрос о точках безусловного экстремума.
Так как для любого номера I , равного 1,2,…,m, справедливо соотношение dψ/dxi =2xi+ λ, то единственной стационарной точкой является точка Мо с координатами Мо (-
λ/2,-λ/2,…-λ/2 ).
Для определения λ используем связи (14.58) из которого получим, что (-λ/2)m+1=0. Таким образом, λ=2/m и единственная стационарная точка Мо имеет координаты Мо(-
1/m, -1/m ,…,-1/m).Поскольку второй дифференциал ФУНКЦИИ Лагранжа (14,59), равный d2Ψ=2[(dx1)2+…+(dxm)2]
всегда положительно определен, то функция (14.57) при наличии связи (14.58) имеет в
точке Мо(—1/т,—1/т, ..., —1/т) условный минимум.
Подставляя координаты точки Мо в (14.57), мы получим, что минимальное значение функции (14.57) при наличии связи (14.58) равно umin=l/m.
§ 5. Отображения банаховых пространств. Аналог теоремы о неявной функции 1. Теорема о существовании и дифференцируемости неявной функции. В § 1 этой главы мы установили теорему 14.1 существования и дифференцируемости неявной
функции, зависящей от числовых аргументов х, у, причем эта функция и = <φ(х, у) находилась как решение уравнения F(и, х, у)~0 в окрестности некоторой точки М0(и, х, у). Ниже мы убедимся, что указанная теорема 14.1 без больших изменений переносится с числовых функций на отображения произвольных банаховых пространств.
4
Предпошлем формулировке и доказательству этой теоремы некоторые обозначения. Символом В мы обозначим некоторое банахово (т. е. полное нормированное) пространство.
Символом N будем обозначать нормированное пространство, через X × Y обозначим прямое произведение множеств X и Y, т. е. множество всевозможных упорядоченных пар (х, у), для которых х Х, y Y.
Всюду ниже под производной некоторого отображения мы понимаем сильную производную, введенную в § 7 гл. 13.
Докажем теорему об отображениях нормированных пространств, обобщающую теорему 14.1 о неявной функции.
Теорема 14.1'. Пусть Nг, N2 и В—линейные нормированные пространства, причем В— банахово пространство, 2— окрестность точки (х0, у0), принадлежащей произведению
пространств Nxu В, a F (х, у) —отображение окрестности ∑ в пространство N2, обладающее следующими свойствами:
а) |
F (х, у) непрерывно в точке |
(х0, у0); х, xo N1, у, Уо В; |
б) |
F(x0, у0) = 0; |
|
в) |
частная производная F'y(x, у) |
(т. е. производная по аргументу у при фиксированном |
элементе х*) существует в 2 и непрерывна в точке (х0, у0), а оператор F'y(x0, y0) имеет ограниченный обратный оператор **) [Fy(xe, Уо)-1.
г) частная производная F'x(x, у) существует в каждой точке окрестности ∑ и непрерывна в самой точке (х0, у0).
При этих условиях в некоторой окрестности∑ 0 точки хв пространства Nt определено отображение у = (р(х): ∑ 0—>В такое, что:
а° F (х, ф (х)) = О в∑ 0 и z/ (х) = ф (х) непрерывно в точке х0;
б° уо = ц>(хо); в° если φ (х)—какое-либо отображение, определенное в некоторой
окрестности∑ точки х0, обладающее свойствами а° и б°, то фх(х) = ф(х) в некоторой окрестности ∑ с: ∑ ^ ∑ 0 точки х0;
г° отображение у = ф (х) дифференцируемо в точке х0 и y' = φ>'(xo) = — [Fy(xo, y0)]-1
Fx(xo, y0).
Доказательство. Без ограничения общности можно считать, что хо = О, уо = О. (В противном случае можно сделать замену хх — х—х0, ух = у—у0, и утверждение сведется к указанному случаю х0 = 0, y0 = 0.)
Согласно условию теоремы окрестность∑ точки (0, 0) принадлежит произведению NxB пространств Nx и В. Очевидно, что окрестность ∑ содержит такую окрестность точки
(0, 0), которая является прямым произведением окрестности ||х||<6 точки О Ν и окрестности ||y||<е точки 0 В.
Итак, можно считать, что хо = О, уо = О и
∑ = {(x,y)eN1xB: ||x||<6, \\у\\<e}. ' \\ Рассмотрим при фиксированном х отображение
Axy = y-[F'y(0, 0)]-1-F(x, у)
окрестности точки 0 g В в пространство В. Подчеркнем, что в силу условий теоремы отображение F (х, у) определено при ||х|]<8, ||г/|]<8 и его значения лежат в пространстве N2. Отображение F'yix, у) определено и непрерывно в точке (0, 0). По условию в) отображение F'y (0, 0): В —+ N2 имеет обратное [F'y (0, О)]"1: JV2—>B. Таким образом, последовательное применение отображений ^(х, у) и [F'y(0, О]"1, т. е. отображение [F'y (0,
0)]~1-F(x, у) определено и его значения лежат в В.
5
Заметим, что точка у = ф (х) является неподвижной точкой отображения Ах (см. гл. 12, § 2) тогда и только тогда, когда F (х, ф(х)) = 0. Таким образом, отыскание и исследование функции у = ц>(х) сводится к отысканию и исследованию неподвижных точек отображения Ах.
Для того чтобы отыскать неподвижные точки отображения Ах, применим принцип сжимающих отображений.
Заметим для этого, что при любом фиксированном элементе х A\ таком, что ||х||<б, отображение Аху дифференцируемо по у в области ||t/||<s, у В, что следует из свойства производной сложной функции (см. гл. 13, § 7, п. 1, свойство 3), причем
(Аху)'у = {Ey)'v-[F'U (О, 0)]-1 F1 (х, у);
здесь Е—единичный оператор. Поскольку, согласно свойству 2 (гл. 13, § 7, п. 1), производная ограниченного линейного оператора есть сам этот оператор, т. е. (Fу)' — F, то мы получим, что
Отображение F'y (x, у) по условию а) теоремы непрерывно в точке (0, 0), поэтому всегда можно найти такую окрестность
|!x||<β<6, ||y||<β<е точки (0, 0) N1xB, в которой
lF'y(0, 0)-Fy(x, У)\\<1/2\\[F”y(00)]-1 \\Следовательно, при [|x:|<β\ ||y||<β получим, что (АхУ)у[|<||[Fy(о, о)]-|Fy(о, о)-F(х, у)\\<1/2.
Всюду ниже будем считать, что ||х|<β, ]]</11<β, и поэтому \\(Axyyy\\< 1/2.
По формуле конечных приращений для отображений при любом фиксированном х, ||х|<р, и любых у1 и уг таких, что \\y1\\<β. получим (см. гл. 13, § 7, п. 2)
Таким образом, А х—семейство сжимающих отображений окрестности \\y||<β точки O B в пространстве В, причем коэффициент сжатия 1/2 не зависит от параметра x Nlt ||X||<B. Для того чтобы применить принцип сжимающих отображений к отображению Ах, следует указать то полное метрическое (или нормированное) пространство, которое при этом отображении переходит в себя.
Укажем это пространство. Зафиксируем произвольное число гх такое, что 0 < ех < р. Покажем, что существует такое число °\(ei)> 0 < ^i (ei) < β. что ПРИ любом x(zNx и |]х|| < ej (ех) (эту окрестность в пространстве Nt обозначим через 20) отображение Ах преобразует
замкнутый шар К (0, ех) с центром в точке 0 и радиуса ej в пространстве β в себя. Действительно, в силу того, что отображение F (х, у) непрерывно в точке (0, 0), и того, что F(0, 0) = 0, для указанного найдется такое положительное число д1 (e), что при ||х|]< ба (j
\\Ax0\\ = l[Fy(0, 0)]-*-F(x, 0)|<||[f;(0, 0)]-4\\F(x, 0)\\<e1.
Далее, если ||х|| < б1 (ех), ||х|| <e1 то в силу того, что отображение Ах сжимающее, и полученной оценки для, ||AxO|| имеем:
Следовательно, Ах преобразует замкнутый шар К (0,e1) пространства В в себя. Элемент х при этом фиксирован и ||х||< Ьг j
Замкнутый шар К (0, ег) является метрическим пространством, причем (в силу замкнутости) полным. В самом деле, В — полное метрическое пространстйо. Всякая фундаментальная последовательность точек уп<сКф, e^czB сходится к точке у0 б В, которая в силу замкнутости К (0, 8Х) принадлежит К (0, гг). Поэтому К (0, ех) — полное метрическое пространство и Ах — сжимающее отображение, определенное на нем. Согласно принципу неподвижной точки (см. гл. 12, § 2, теорема 12.3) получаем, что при каждом xg20 найдется единственная точка у = =Ф (х) в шаре /((0, е3), неподвижная относительно отображения Ах. Для этой точки справедливо соотношение
Ах Ф (*) = * (х) = Ф (х)-[F'y (0,0)]-* F (х, Ф (*))
Или F(x,φ(x))=0,
если
\\x\\1<δ(ε1)
Следовательно, функция у=ф(х) удовлетворяет уравнению
6
F (х, ф(х)) = 0. Эта функция непрерывна в нуле, так как по любому положительному е1 < β, мы можем найти такое 8t (e^), что при ||Х||<61(Е1) отображение Ах переводит шар К (О, &х) в себя, т.е. единственная неподвижная точка г/ = ф(х) этого отображения при xg20 принадлежит шару К(0, Ej), т.е. удовлетворяет условию || ф (х) |
<ε1.
Утверждение а° полностью доказано. Далее, поскольку
Ao0 = 0-[F'y(0, 0)]-*F(0, 0) = 0,
то в силу единственности неподвижной точки имеем при х = 0 г/о=ф(О) = О. Тем самым установлено утверждение б°.
Далее, если фх (х)— отображение, удовлетворяющее условиям а° и б° в некоторой окрестности ∑ 1точки 0 Nlt то найдется такое 62(6!), что || <Pi (*) || ^ Е, при ||х||< Ь2(е1).
При ||х||< < min (6j (ej, б3 (EJ) одновременно будут выполнены соотношения || Ф (х) |К ЁХ и || фх (х) К ЕХ. В силу того, что F (х, фх (х)) = 0, будет справедливо равенство
Л*Ф! (х) = Фх (х) - [F'y (0, 0)]-i F (х, ф1 (х)) = Фх (х)
при любом х таком, что \\x\\ < min (81 (EJ, S2(e1)).
Следовательно, ц>1 (х)—также неподвижная точка отображения Ах, принадлежащая шару К (0, Ej). Однако неподвижная точка может быть только одна, поэтому ц>1 (х)=ф (х) в окрестности
∑ = {х, ||х||< min (б(вх), б2 (6l))} ∑∩ ∑
Тем самым доказано утверждение в0.
Осталось установить утверждение г° о дифференцируемости неявной функции. Обозначим через L линейный ограниченный оператор, действующий из Nt в В по правилу
L = q>'(O) = -[F;(O, 0)]-i.F'x(0, 0).
Проверим, что этот оператор L является производной отображения г/=ф(х) в точке 0. Напомним, что для этого необходимо существование для каждого Е > 0 такого б > 0, что для любого х, удовлетворяющего условию ||х||<б, выполнено неравенство
Учитывая, что ф(0) = 0, и используя выражение для L, запишем соотношение
φ(x)-φ(0)-Lx=φ(x)+[Fy(0,0)]-1Fx(0,0)x
Поскольку F(х, ф(х)) = /;'(0, 0) = 0, то с помощью формулы конечных приращений для отображений получим, обозначая буквой у функцию ф(х):
, 0)]-i\\\\F(x,y)-F(0, 0)-F'x(0, 0)x-Fy(0,
(О, 0)1 -х II ■ Г sup
Lo < е, е, < 1 sup \\Fy(Qx, 9хг/) — о < е, е, < 1
F'x(Qx, Qiy)-F'x(0,0)
где величина ц может быть сделана сколь угодно малой (в силу непрерывности в точке (0, 0) производных F'x и F'y), если величина б достаточно мала. Таким образом, \у—Lx||^ ц
(||х| + \\у||) ^ ^Л (IIхII + |£*|| + \У—^Х1|)- Отсюда при достаточно малом η
получаем, \\у — Lx||< т] (1 — ц)'1 (\ +|L||)||x||. Достаточно выбрать т] так, чтобы было выполнено неравенство Дифференцируемость отображения у = ф (х) в точке 0 доказана, и утверждение г° установлено.
Таким образом, теорема 14.1' полностью доказана ***).
2. Случай конечномерных пространств. Рассмотрим важный частный случай, когда нормированное пространство N1 совпадает с пространством Ет, а пространства В и N2 совпадают с Е" ****). В качестве следствия теоремы 14.1' получим теорему о неявной функции для этого частного случая.
Выберем в пространствах Ет и Еп базисы и запишем отображение F (х, у) в координатной форме:
F1=F1(x1,…xm,y1,…yn),
……………………….
7
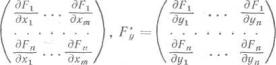
Fn=Fn(x1,…xm,y1,…yn),
где (Xj, ..., xj )= x—точка пространства Ет, (уг, ...,уп)
точка пространства Е", причем точка (Flt ..., Fn) принадлежит также Е".
Подчеркнем, что отображение F(x, у) определено на прямом произведении пространств NxxB или в данном частном случае на прямом произведении ЕтхЕп. Если фиксировать переменную у, положив ее равной у0, то мы получим функцию, определенную *). на некотором множестве Е™а—сечении ЕтхЕ". Отображение F(x, г/0) представляет собой частичное отображение по переменной х (по отношению к исходному отображению F(x,
у)).
Если в некоторой точке хо Е™а это частичное отображение F (х, у0) дифференцируемо,
то его производная в этой точке х0 называется частной производной исходного отображения F(х, у) в точке (хв, у0) {или частным производным отображением) по переменной х. Обозначается эта частная производная символом Fx (х0, у0) или ■—*"' Уо' (иногда DxF(x0, y0)). Ясно, что наши рассмотрения пригодны и в общем случае нормированных пространств Nlt В, а не только в случае конечномерных пространств Ет и
Е".
Замечание. Нетрудно, так же как и в случае функций многих переменных, доказать, что если отображение F(х, у): ЛГхх ХВ—>iV2 дифференцируемо в точке (х0, у0), то в этой точке у него есть все частные производные отображения и справедливо
соотношение dF (x0,y0)= (dF(x0,y0)/dx)dx +(dF(x0,y0)/dy)dy
Здесь
dF (х0, у0)—дифференциал Фреше от функции F (х, у) в точке (хо,yо); — частные производные отображения F (х, у)
в точке (х0, у0), a (dx, dy) элемент касательного пространства К1х„Уа)^хВ**). Вернемся снова к изучению отображения F (х, у): Ет х Е" —*- Е". Согласно рассмотрениям п. 8 § 7 гл. 13 частные производные
отображения F'x: Nr F'x: Em-+ F'y: En-Ns F'y: B—+N^ или, что то же самое, уЕп задаются матрицами
F’y=
Непрерывность отображений F'x и F'y (операторов в конечномерных пространствах, задаваемых матрицами), как известно из курса линейной алгебры, равносильна непрерывности всех элементов соответствующей матрицы. Обратимость линейного отображения Fy(x0, у0): Еп—^Еп равносильна невырожденности матрицы, задающей это преобразование.
Теперь мы подготовлены к тому, чтобы сформулировать теорему 14.Г в случае отображения F(х, у): ЕтхЕп—>Еп.
Теорема 14.1. Пусть Ет и Е"—два конечномерных пространства размерностей тип соответственно, ∑ —окрестность точки (х0, у0), л;0 = (х1, ..., хт), ув — (у17 ...,уп), лежащей в произведении пространств Ет и Еп и F (х, у)—отображение Ис:ЕтхЕп в
пространство |
Е", обладающее свойствами: |
||
а) |
F(x, у) |
непрерывно в точке (х0, у0); х, хо Ет; у, уо Еп (т. е. в точке (х0, у0) |
|
непрерывны все координаты F,-, i = I, ..., п); |
|||
б) |
F(x0, |
г/0) = ° (т.е. Fx(xx, ..., хт, уи •■-, уп) = 0, ... |
|
..., |
Fn(xlf |
..., хт, уг, ..., г/„) = 0), где |
|
в) частная производная |
|||
|
|
|
( (dF1(x,y)/dy1…(dF(x,y)/dyn) |
F’y(x,y)= |
(…………………………… ) |
||
|
|
|
((dF(x,y)/dy1…(dF(x,y)/dyn ) |
|
|
|
8 |
существует в каждой точке окресности 2 и непрерывна в точке (х0, у0) (т. е. в точке (х0, у0) непрерывны все элементы указанной матрицы), а отображение
( (dF1(x0,y0)/dy1…(dF(x0,y0)/dyn) F’y(x0,y0)= (………………………………… )
((dF(x0,y0)/dy1…(dF(x0,y0)/dyn )
не вырождено (т. е. определитель указанной матрицы отличен от нуля);
700
г) частная производная
( (dF1(x0,y0)/dy1…(dF(x0,y0)/dyn) F’y(x,y)= (………………………………… )
((dF(x0,y0)/dy1…(dF(x0,y0)/dyn )
существует в каждой точке окрестности 2 и непрерывна в точке (х0, у0) (т. е. в точке |
||
(х0, у0) непрерывны все элементы указанной матрицы). |
т |
|
При этих условиях в некоторой окрестности 20 |
|
|
точки х0 g Е определено отображение |
||
г/=ф(х) (т. е. определены функции Ук = {$>к{х1> |
хт)> k—\, |
..., п) такое, что: |
a0 F(x, <р(х)) = 0в 20 (т.е. Pt(xlt ..., хт, yit .... уп)^0, 1 = 1, |
...., п) и у =ф (х) непрерывное |
|
точке х0 (т. е. координаты |
|
|
<Pi (х).....фй (х) отображения ц> (х), х = (хи . .., хт) непрерывны |
||
в точке х0); |
|
|
б° г/0 = ф(х0) (т.е. yk = q>k(x13 ..., хт), k = \, ..., п)\ в° если ц>1(х) — другое |
||
отображение, определенное в некоторой окрестности 2± |
точки х0, обладающее |
|
свойствами а° и 6°, то Фг (я) = Ф (х) в некоторой окрестности "Scl^n^o точки х0; г° отображение у = (р(х) дифференцируемо в точке х0 и
, уо)]-К F'x(x0, уо) =
( (dF1(x0,y0)/dy1…(dF(x0,y0)/dyn)-1
-(………………………………… ) * ((dF(x0,y0)/dy1…(dF(x0,y0)/dyn )
( (dF1(x0,y0)/dy1…(dF(x0,y0)/dyn)
*(………………………………… ) ((dF(x0,y0)/dy1…(dF(x0,y0)/dyn )
Замечание. В случае, если Еп одномерно, т. е. Е" совпадает с Е1, мы получим всего одно скалярное уравнение F(xlt ... ■ •;» хт, у) = 0, где х = (хи ..., xj—точка из Ет, у £ Е1 — числовой аргумент. В этом случае отображение F'y состоит только из
одного элемента -у-, и поэтому (F'y)-i—\
Поскольку в этом случае -j— = tх = ( -г— , .. ., -~-— ) , то, согласно утверждению г° теоремы 14.1, получаем, что y’=(dy/dx1,…,dy/dxn)= -(dF/dx1)-1(dy/dx1,…,dy/dxm)
3. Особые точки поверхности в пространстве п измерений. Обратное отображение. В п. 3 § 1 этой главы мы рассматривали понятие особой и обыкновенной точки поверхности в трехмерном пространстве Е3. Рассмотрим теперь обобщения этих понятий на случай поостранства любого конечного числа измерений.
9

Пуст. y = f(x) — отображение окрестности точки х0 пространства Ет в пространство Еп, дифференцируемое в точке х0. Если в пространствах Ет и Еп выбрать базисы, то отображение у = / (х) может быть записано в координатной форме [х = (х1, х2, ..., хт)]. y1=f1(x1,…,xm)
…………………
yn=fn(x1,…,xm)
Рангом отображения y = f(x) в точке хо==(х1, вается число, равное рангу матрицы
., хт) называется число равное рангу матрицы
Обычно ранг отображения f (х) в точке х0 обозначается символом rang/(x0). Ясно, что rang /(x0X rain (m, п).
Определения. Точка х0 пространства Ет называется особой (критической, сингулярной) точкой отображения f(x) некоторой окрестности этой точки в пространство Еп, если ранг этого отображения в точке х0 меньше наименьшего из чисел т и п, т. е. если rang
/(х0) < min (m, п).
Если в точке х0 выполнено соотношение rang / (х0) = min (m, га), то точка хп называется обыкновенной или неособой для
отображения у=f(x) Пусть ха Еm x0=(x1,…,xm ). Рассмотрим соотношение
оо
F(Ху, ..., хт), где F—числовая непрерывно дифференцируемая функция, F: Ет—+ Е1. Предположим, что точка х0 = (хх, ■ ■., хт не является особой для функции F. Поскольку в этом случае матрица, определяющая ранг отображения, состоит из одной строки
dF(x0) dxx
dF (x0) dxm то сформулированное выше условие того, что точка х0 не является особой для отображения F(х) (т.е. условие xangF — = min (m, 1) = 1), означает, что хотя бы одна из частных производных F в этой точке отлична от нуля. Пусть ради определенности
Ф0. Поскольку F(xo) = O, то по теореме 14.1" о неявном отображении переменную хт в окрестности точки
xo = (xi.....хт) можно выразить в виде функциональной зависимости
Хт = f(х 1, …, Хт — 1)
Таким образом, в окрестности неособой точки мы разрешили функциональную систему уравнений, состоящую из одного уравнения, зависящего от т переменных.
Пусть теперь в некоторой окрестности точки х0 = (xlt ..., хп+т) пространства Еп+т задано обращающееся в нуль в этой точке отображение F: Еп+т—*Ет, т > 1, указанной окрестности в пространство Ет непрерывное в этой окрестности и обладающее в ней частными производными первого порядка по всем переменным, непрерывным в самой точке х0. Тогда, если точка х0 не является особой, то rang F (х0) = т, т.е. найдется хотя бы один минор порядка т, отличный от нуля. Пусть это будет, например, минор . Тогда по теореме о неявной функции
14.1" уравнение F(x) — O, т. е. система разрешима в указанной окрестности точки х0 относительно пере-! менных хг, ..., хт, т.е. существуют единственные функции являющиеся решением системы функциональных уравнений (14.60); эти функции будут непрерывны в некоторой окрестности точки х'о = (xm+i, • • •» Хт+п) и дифференцируемы в этой точке. (Если предав-положить, что частные производные -^J- непрерывны и в некоторой окрестности точки хв, то и функции фх, ..., фот будут
дифференцируемы в некоторой окрестности точки (хт+1, ..., xm+n), см. сноску к теореме 14. Подчеркнем, что условие неравенства нулю якобиана D(F1,…,Fm)/D(x1,…,xm)
10
означает при |
принятых нами определениях, что |
отображение F(x', х'о): Ет—уЕт |
(х'а—фиксированная точка) имеет ранг в точке |
|
|
(хи .... хт) = х', равный т: rangF(x', x'0)=min(m, |
m) = tn, |
|
т. е. означает, что точка х' является неособой для отображения |
||
г (х , х0) \hm |
> Ьт; выше х0 = (xm+i, .. ., хт+п), х = (xlt . . ., хт). |
|
В качестве еще одного следствия теоремы 14.Г о неявном отображении является |
||
следующая теорема об обратном отображении (об обратной функции) (см. также п. 4 первого параграфа этой главы).
Теорема. Пусть F: 2^,/V—отображение открытой окрестности 2 точки х0 банахова пространства В в нормированное пространство N. Пусть отображение y = F(x) дифференцируемо в 2, F' (х) непрерывно в точке х0 и оператор F' (х0) обратимый. Тогда найдутся окрестность 2Х точки х0, 'Z1dB, и окрестность 22 точки yo = F(xo),
S2cA^, такие, что отображение F: 2Г—*Б2 взаимно однозначно отображает 2Х на 22, а обратное отображение F'1: 22—^ непрерывно в 22 и дифференцируемо
в точке х0, причем (F'1)' (yo) — [Fr (х,,)]'1.
Для доказательства этой теоремы достаточно применить теорему 14.Г о неявной функции (о неявном отображении) к отображению
G(y, x) = F{x)-y,
определенному на множестве Nх2, HczB, и принимающему значения в пространстве N. Действительно, в этом случае для G (у, х) выполнены все условия теоремы 14.Г: G (г/0, х„) = 0; G(y,x) непрерывно в точке (у0, х0); G'x(y, x) = F'(x), G'y=—E, E—единичный оператор, поэтому G'y и G'x определены в Nх% и непрерывны в точке (у0, х0); наконец, G'x(y0, xo) = F'(xo)—обратимый оператор. Поэтому, применяя теорему 14.Г к отображению G(y, x), мы можем утверждать, что в некоторой окрестности 22 точки уо€ N существует функция x = F~x (у), которая непрерывна в этой окрестности 22; справедливо соотношение xo = F~1(yo); функция x(y) = F~1 (у) дифференцируема в точке у0, причем
Отображение x = F~l(y) осуществляет взаимно однозначное отображение окрестности 22 на 2^ и является обратным по отношению к отображению y = F(x). Если предположить, что отображение y = F(x) непрерывно дифференцируемо в некоторой окрестности точки х0, то отображение x = F~1(y) будет диффеоморфизмом (т. е. будет взаимно однозначным и дифференцируемым отображением 22 на 2J.
Геометрически это утверждение можно истолковать так: множество G (у, x) = F(x)— г/ = 0, заданное как график отображения y = F(x), в некоторой окрестности (у0, х0) точки из пространства NxB можно изобразить как график отображения x = F~x(y), заданного в некоторой окрестности точки у0 £ N.
В случае, если пространства В и N совпадают с пространством Ет, т. е. В — N = Ет теорема об обратном отображении утверждает, что если задано отображение y = F (х) или в координатной форме причем функции Fh i = 1, т дифференцируемы в окрестности точки хо — (х19 ..., х-т) и их частные производные непрерывны в yo = F (xQ); якобиан от нуля, то существуют окрестности 2tсЕт, 22с:£я точек xo€2j и yg £ 22 соответственно, которые взаимно однозначно соответствуют друг другу при помощи отображения у = F(х): 2Х—>22, причем существует гомеоморфное отображение х = /7~1 (у): 22 —>-2г
окрестности 22 на окрестность 2,, обратное по отношению к F, дифференцируемое в точке уо = (у19 ..., ут) и (Если предположить, что отображение y = F(x) непрерывно дифференцируемо в некоторой окрестности точки х0, то отображение x = F~x(y) будет
диффеоморфизмом).
Замечание. Условие обратимости отображения F' (х0), фигурирующее в теореме об обратном отображении (или в случае отображения пространства Ет в Ет неравенство нулю якобиана является лишь достаточным условием для и (х%, ..., хт) существования обратного отображения х — F'1 (у). Обратное отображение может существовать и в случае, когда это условие не выполнено. Например, если y~F(x) = x3: E1—>-E1, то в точке нуль якобиан равен нулю, но обратная функция x=f/y существует. Однако, если в точке х0
11
якобиан равен нулю, то обратная функция, если она и существует, не может быть дифференцируемой в соответствующей точке у0, где yo = F(xo).
4. Условный экстремум в случае отображений нормированных пространств. Точно так же, как и для числовой функции нескольких переменных, нетрудно получить решение задачи об условном экстремуме и в случае отображений нормированных пространств. Для этого мы воспользуемся необходимым условием экстремума для функционалов (см. гл. 13, § 8,
п. 1).
Утверждение. I7ycmbF(x,y)—вещественный функционал, определенный в некоторой окрестности 2 точки (х0, у0) произведения Вг X В2 двух банаховых пространств В1 и В2 и дифференцируемый в этой точке (х0, у0). Пусть G (х, у)—отображение окрестности 2 в нормированное пространство N, непрерывно дифференцируемое в окрестности 2, причем G (х0, г/0) = 0- Если отображение G'y(x0, у0)—обратимый оператор, то для того, чтобы функционал F (х, у), рассматриваемый на подмножестве 2, определяемом условием G (х, г/)=0, имел в точке (х0, у0) локальный экстремум, необходимо, чтобы существовал такой функционал А, отображающий нормированное пространство N в вещественную ось, что
F'(x0, yo)-AG'(xo, JO = <)•).
(Последнее условие можно трактовать как необходимое условие экстремума, функционала Лагранжа W=F(x, у)—AG (х,у)—0. Роль множителя Лагранжа К здесь играет функционал А.)
Доказательство. Рассмотрим соотношение G (х, у) — 0 в окрестности 2 точки (х0, уа)£ВлхВ2. По теореме о неявном отображении уравнение G (х, у) = 0 можно разрешить относительно аргумента у и тем самым множество точек (х, у), удовлетворяющих условию G (х, г/) = 0, в окрестности 2 точки (х0, у0) можно представить в виде элементов множества (х, у(х)), где у (х)-—непрерывно дифференцируемая в некоторой окрестности точки х0
функция и у(хо) = уо.
Таким образом, задача об условном экстремуме для функционала F (х, у) при условии G (х, у) = 0 свелась к задаче нахождения локального экстремума для функционала Ф (х) = F
(х, у(х)).
*) То есть в точке (х0, у0) выполнены три соотношения: F'x(x<t, У о)—AG'X(XO> ,(/O) = O,
Fy(xu, ijo)—AGy(xo, г/0) = 0, G(x0, г/о) = О.
Воспользуемся необходимым условием экстремума для дифференцируемого функционала
Ф(х). Согласно результатам п. 1 § 8 гл. 13 получим, что Ф' (х0) = 0. Однако
'o))+Fy(Xo, У(ХО))У'(ХО).
Поэтому условие Ф' (х0) = О равносильно выполнению равенства К(х„, y(xo)) + F'y(xo, y(xo))y'(xo) = O.
Учитывая, что у(хо)=уо, у'{хо) =—[Gy(x0, «/„H^-G^x,,, y0) и что линейный функционал
A = F'y(xg, yo)[Gy(xo, г/0)]-1
действует из пространства N в числовую ось Е1 (действительно, [G'y(x0, г/0)]-х€(Л^-^Б2), F'y(x0, у0) £ (В2 —+ Е1)), имеем, во-первых, что Fx(x0, уд)—AGx(x0, г/0) = 0, а, во-вторых, из равенства получим, что Равенства
F'x(x0, У0)—Л-Сх(х0, уо) = О, |
,, |
F'y(xa, yo)—AGy(xo, г/0)=0, |
_ ., |
G (х0, г/0) =0,
очевидно, и завершают доказательство.
Если рассматривается частный случай отображения F (х, у) окрестности Е точки (х0, у0) произведения двух конечномерных пространств Ет х Е" в пространство Ех при условии, что G (х, у) = 0, хо,х£Ет, у9, у£Еп, G (х, у): 2—>Еп, то в координатной форме необходимое условие экстремума, очевидно, имеет вид
Gp(xlt ..., хт, уг, .... г/„)==0, гдеА:=1,2, ..., т,/,>= 1, 2, ...,n,G = (G1, ...,Gn),(K.....К) —
набор вещественных чисел, хо = (х1, ..., хт), уо = {уи ..., уп)> см. также формулу
(14.55).
12
В частности, если отображение G (х, у) переводит окрестность S в вещественную ось, т. е. функция G (х, у) вещественнозначная (G: 2—^Е1), мы получаем уже найденное нами ранее необходимое условие экстремума функции F (х, у) при условии, что функция G (х, у) — 0. Заметим, что в этом случае очевидно, что вектор (Хи ..., %п) заменяется одним вещественным числом X—множителем Лагранжа.
Дополнение 1 к главе 14
КРИВИЗНА ПЛОСКОЙ КРИВОЙ. ЭВОЛЮТА И ЭВОЛЬВЕНТА
Если плоская кривая L определяется уравнением вида F (х, у), причем функция F (х, у)
дифференцируема в некоторой окрестности точки Мо = (х0, у0) (или Мо (х0, у0)) этой
кривой и имеет в указанной точке непрерывные частные производные по х иг/, то точка |
||||
Мо, согласно определению § 1 гл. 14, является особой, если обе |
||||
dF (х у) |
dF (х у) |
. |
. |
: |
|
||||
точке (х0 |
, у0) равны нулю. |
|
|
|
dF (х, у) |
dF (х, у) частные производные |
|
||
Если хотя бы одна из указанных частных производных функции F(х, у) отлична от нуля,
то точка (х0, у0) является обыкновенной.
Если же плоская параметризуемая кривая L задана при помощи уравнений
х = Ф(0, y = ^{t),
причем функции х = ср(/), y = ty(i) имеют при t — t0 непрерывные производные, то точку Мо = (хв, г/0) (или М0(х0, у0)) кривой L, координаты х0 и у0 которой соответственно равны <p(t0) n ty(t0), назовем особой, если одновременно выполнены соотношения ф'(*о) = О и 'Ф'(^о):=О- Если же по крайней мере одна из производных ф' (t0) и ty' (t0) отлична от нуля,
то точка Мй называется обыкновенной.
Легко убедиться, что если точка Мо кривой L является обыкновенной, то в некоторой окрестности этой точки кривая L представляет собой либо график некоторой дифференцируемой функции y = f(x), либо график некоторой дифференцируемой функции x = g(y).
Действительно, если кривая задана уравнением F (х, у)=0, то указанный факт—следствие теоремы 14.1 о неявной функции. Если же кривая L задана при помощи уравнений x = q>(t), y = ty(t), то из того, что одна из производных ф'(/) или ij/ (t) не равна нулю в точке t0, например (р'^0)ф0, и эта производная непрерывна в точке t0, вытекает, что Ф'(^0) не равна нулю в некоторой окрестности точки t0. Тогда функция x = ff(t) является строго монотонной в этой окрестности. Поэтому существует дифференцируемая монотонная обратная функция / = ц>~1{х).
Тогда, очевидно, кривая L представляет собой график дифференцируемой функции y = f(x) = гф(ф~1 (х)) в некоторой окрестности точки Мо.
Пусть уравнения x = (p(t), y = ty(t) задают параметризуемую кривую L.' Будем считать, что кривая L не имеет точек самопересечения и участков самоналегания. В этом случае в любой точке М кривой L можно выбрать положительное направление. Будем считать положительным направлением в данной точке М кривой L то направление, в котором будет перемещаться точка М при увеличении параметра t.
Выберем на кривой некоторую точку Мо, отвечающую значению параметра t0, и предположим, что эта точка является обыкновенной точкой кривой. Согласно рассуждениям, проведенным выше, в окрестности точки Мо кривая L представляет собой график функции вида либо y = f{x), либо х = g(y), причем функции f (х) и g(y)
дифференцируемы в этой окрестности точки Мо, следовательно, существует касательная
к кривой L в точке Мо.
13
Договоримся называть положительным направлением на касательной то направление, в
котором будет перемещаться при увеличении параметра точка, представляющая собой проекцию на касательную точки кривой L.
Предположим теперь, что все точки кривой L, расположенные в окрестности точки Мо,
являются обыкновенными, а касательная к кривой L в точке Мо имеет положительное
направление. Пусть М — некоторая точка из окрестности точки Мо, отвечающая большему значению параметра, чем точка Мо.
Определение. Углом смежности участка М0Мкривой L называется угол между положительно направленными касательными к кривой L в точках М и Мо, взятый со
знаком плюс в случае, если касательную в точке Мо для совмещения кратчайшим путем с
касательной в точке М следует повернуть против часовой стрелки, и со знаком минус—в противном.
Введем понятие средней кривизны.
Определение. Средней кривизной участка МаМ кривой L называется отношение угла
смежности этого участка к длине самого участка МаМ.
Поскольку точка Мо фиксирована, то средняя кривизна участка М0М является функцией
точки М или функцией параметра t. Обозначим среднюю кривизну участка МВМ кривой
L через kcv(M0M) (или kcp(t)).
Естественно, возникает вопрос о рассмотрении предела функции kcv (М0М) при стремлении точки М вдоль кривой L к точке АТ„ (или, что то же самое, при стремлении
параметра / к tQ).
Определение. Кривизной кривой L в данной точке Мо называется предельное значение средней кривизны участка кривой М0М при стремлении точки М вдоль кривой L к точке Мо. Обозначается кривизна кривой L в точке Мд символом
k(M0)= lim kcv(M0M)= lim k (t).
Нетрудно получить формулы, позволяющие находить кривизну кривой L, заданной при помощи уравнений x = (p(t), y = ty(t) или при помощи уравнения y = f(x).
Рассмотрим случай, когда кривая задана уравнениями x = <p(i), y = ty(t), пусть функции ф(/) и ty(t) имеют в точке t0 вторые производные.
Пусть х и х—значения первой и второй производных функции x = q>(t) в точке t0, a x-j- Ax—значение первой производной этой функции в точке t0JrAt, где At— некоторое приращение параметра t. Таким образом, Ах—приращение первой производной функции x = q>(t). Пусть у, у я у + Ау—соответствующие величины для функции y = ty(t).
Будем считать, что точка Мо фиксирована и отвечает значению параметра t0, а точка М отвечает значению параметра to-\-At. Поэтому угол смежности участка М0М и длину этого участка можно рассматривать как функции аргумента At. Обозначим длину участка М0М через l(At), а угол смежности этого участка через a (At). Нам надлежит вычислить величинуAt.
Если обозначить через ф0 и ф углы наклона к оси Ох касательных к кривой L, проведенных через точки Мо и М соответственно, то, очевидно, чтоа(А/) = ф — ф0, а
также, 4Totga(A/) =
= tg (Ф — Фо) = Д^^о • Поскольку tg Фо = Л-, tg q>=(y'+Ay) x
Х(х +Ах)"1, то после очевидных преобразований несложно заключить, что Поскольку функции x — cp(t), г/ = -ф(/) имеют в точке t0 вторые производные, то первые производные этих функций непрерывны в точке t0, поэтому Ау—*0, Ах—+0 при t—+to (At—+O). Но тогда tga(A/)^—*0 при At—э-0, а поэтому и a (At)—>-0, если At—*0. Следовательно,limAt -*0
l(At) = J Vх* (т) + у* (т) dtt
то по формуле среднего значенияЗначит,k{M0)=-х •Д/-у- ∑ хТак как функции Х = Ц>(Г), имеют в точке t0 вторые производные, то lim -т-т- = х, lim -~ — у. Из непрерывности
14
первых производных функций х = ф(/), ?/ = ij;(/) вытекает, что при At—у 0 AyПоэтому хг/ — ху Если кривая L представляет собой график дважды дифференцируемой функции y
= f(x), то, полагая x — t, y — f(t), получаем для кривизны следующую формулу:
А(Л1.)=- -Г(Х) -
Радиусом R кривизны кривой L называется величина l/k, где k—кривизна, а центром кривизны—точка нормали *) к кривой L, которая отстоит от данной точки кривой L в направлении вогнутости L на расстоянии R.
Если рассматриваемая кривая L представляет собой дугу окружности радиуса г, то, как нетрудно убедиться, кривизна k равна величине 1/г, а радиус R кривизны такой кривой L равен радиусу окружности г.
В заключение введем еще два понятия, тесно связанных с рассматриваемым в этом дополнении материалом.
Определение. Геометрическое место центров кривизны данной кривой L называется эволютой кривой L.
Кривая L по отношению к своей эволюте называется эвольвентой.
Ясно, что, например, эволютой окружности является множество, состоящее всего из одной точки — центра окружности. Окружность по отношению к своему центру является эвольвентой.
15
