ВАРИАНТ V

1.Каким основным свойством множество всех действительных чисел отличается от множества всех рациональных чисел?

2.Построить пример расходящейся последовательности, имеющей только одну предельную точку.

3.Найти область определения функции

y= arccos11+− xx .

4.Найти следующие пределы:

1) lim (s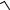in 1+ x −sin 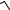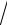x);

x→+∞

2)lim1− cos x2cos 2x ;

x→0 x

3) lim tgxtg 2x .

x→π4

5. Найти производные следующих функций:

1) y = 12 tg 2 x + ln cos x ;

6. Исследовать функцию и построить её график:

y= e−x2

7.От канала шириной а под прямым углом к нему отходит канал шириной в. Оба канала прямолинейны. Найти наибольшую длину бревна, которое при сплаве из одного канала в другой не застрянет на повороте?

8.Доказать, что если в некотором интервале (a,b) функция f(x) имеет производную f’(x)>=0 и эта производная, причём знак равенства имеет место лишь в конечном числе точек интервала (a,b), то функция f(x) в интервале возрастает.

ВАРИАНТ VI

1.Сформулировать определение иррационального числа.

2.Найти предел последовательностей:

3. Найти область определения функции:

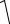
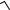
y= 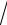1− x − 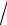x − 13 .

4.Найти следующие пределы:

2) y = eax a sin bx −b cosbx . a2 + b2

6.Рычаг второго рода имеет точку опоры на конце и уравновешивается силой f на другом конце. На расстоянии a от точки опоры подвешен груз p. Вес единицы длины рычага равен m. При какой длине рычага сила будет наименьшей?

7.Исследовать функцию и построить её график:

y = x2 + 1 .

2 x

8. Для какого интервала (0,x) приближённое равенство

cos x ≈1− x2 2

будет иметь место с точностью до 0,000001?

ВАРИАНТ VII

1.Доказать, пользуясь определением предела последовательности, что

lim 1 = 0,

x→∞ n!

т.е., считая заданным ε>0, найти такое N, что при всех n>N будет выполняться неравенство:

1

n!<ε.

2.Найти предел последовательности:

lg22 , lg33 , lg44 ,..., lgnn ,... .

3.Найти область определения функции:

y= 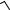sin x + cos x −1 .

4.Найти следующие пределы:

1

sin x x−a

3) lim .

x→a sin a

5.Найти производные следующих функций:

6.Исследовать функцию и построить её график:

− 1

y = e x2 .

7.Чашка имеет форму полусферы радиуса а. В неё опущен стержень длины l>2a. При каком положении стержня его середина находится ниже всего (положение равновесия)?

8.Сколько членов надо взять в формуле Тейлора, чтобы

π

вычислить значение sinx в интервале (0,18 ) с точностью

до 0,000001? Написать соответствующую приближённую формулу.