11.2. Реакция дискретных динамических систем на конечномерные экзогенные воздействия

Рассматривается линейная дискретная система (11.2), в которой экзогенное воздействие формируется с помощью автономной конечномерной ДС вида (10.37), имеющей ВМО вида

; (11.62)

Построение аналитического представление реакции дискретной системы (11.2) опирается на возможности матричного уравнения Сильвестра и строится по той же схеме, что и в случае непрерывных ДС. В связи со сказанным процедуру формирования аналитического представления реакции дискретных динамических систем на конечномерные экзогенные воздействия представим конспективно в виде алгоритма 11.2.

Алгоритм 11.2(а11.2)

1. Формирование векторно-матричного описания (11.2) исследуемой дискретной системы – матриц ;

2. Формирование векторно-матричного описания (11.62) источника дискретного конечномерного экзогенного воздействия – матриц ;

3. Формирование агрегированной автономной дискретной системы

(11.63)

где

(11.64)

позволяющей для агрегированного вектора состояния записать

(11.65)

4. Введение априорной «гипотезы» о соблюдении векторного подобия

(11.66)

где –- матрица подобия;

5. На основе (11.2), (11.62) и (11.66) установление того, что матрица удовлетворяет матричному уравнению Сильвестра вида (11.28), записываемого для дискретного случая в форме

; (11.67)

6. Представление матрицы вида (11.64) на основе уравнения Сильвестра (11.67) в форме

; (11.68)

7. С использованием положений утверждения 11.3 представление показательной (степенной) функции в блочной матричной форме

; (11.69)

8. Формирование аналитических представлений векторных переменных исследуемой дискретной системы (11.2) и источника дискретного конечномерного экзогенного воздействия (11.62) с использованием векторно-матричных зависимостей (11.63), (11.64) на основе показательной функции (11.69) в форме:

(11.70)

9. На основе полных представлений векторных переменных задачи в форме (11.70) построение аналитических описаний:

Вынужденныx составляющих по состоянию, входу и ошибке

(11.71)

. (11.72)

Установившихся составляющих по состоянию, выходу и ошибке

(11.73)

(11.74)

Переходных составляющих по состоянию, выходу и ошибке

(11.75)

Из сравнения представлений для (11.73) и(11.70) становится понятным математическое «содержание» матрицы, состоящее в том, что она представляет собой матрицу подобия между процессамипо вектору состояния в источнике конечномерного дискретного экзогенного воздействия (ИКДЭВ) и установившейся составляющей вектора состояния исследуемой дискретной динамической системы так, что устанавливаются соотношения

Как и в случае непрерывных систем, остановимся теперь на ситуации, когда ИКДЭВ формирует типовые дискретные экзогенные воздействия, ограничившись случаями: ступенчатого и гармонического дискретных экзогенного воздействий. Первое типовое воздействие используется для оценки динамических свойств исследуемой ДС по кривой переходного процесса, второе – по амплитудным частотным характеристикам.

Случай 11.3 (Сл11.3) ступенчатого дискретного экзогенного воздействия характеризуется матрицами имодельного представления ИКДЭВ (12.62) в силу (11.45), имеющими вид

. (11.75)

Подстановка матриц вида(11.75) в уравнение Сильвестра (11.67) дает

, что позволяет для матрицы записать

(11.76)

Матрицы вида (11.75) ивида (11.76) дают для степенной матричной функции, записанной в форме (12.69) представление

(11.77)

Подстановка матричной степенной функции вида (11.77) и выделение из полного движения вынужденной составляющей по вектору состояния и выхода исследуемой системы дает

(11.78)

(11.79)

В выражениях (11.78) и (11.79) матрицы

(11.80)

(11.81)

представляют собой соответственно матричные переходные функции по состоянию и выходу дискретной системы (11.2) Если возникает необходимость скаляризации задачи, состоящей в исследовании динамических свойств го сепаратного канала дискретной ДС, связывающегой выходсм входом, то в этом случае впереходной матрице по выходу (или просто впереходной матрице) выделить й элемент

(11.82)

где соответственноя строка матрицы выходаий столбец матрицы входа

Как будет показано в разделе 13 книги, глобальная скаляризация векторных процессов в системах типа «многомерный вход – многомерный выход» строится с помощью мажорант и минорант, являющихся для максимальным и минимальным сингулярными числами переходной матрицы

Случай 11.4(Сл11.4) гармонического дискретного экзогенного воздействия характеризуется матрицами имодельного представления ИКДЭВ (11.62) в силу (10.49) – (10.50), имеющими вид

, (11.83)

. (11.84)

Прежде, чем формировать аналитическое представление реакции динамической системы на дискретное гармоническое воздействие следует заметить, что частотные методы применяются для исследования установившихся составляющих движения системы, которые для векторов состояния и выхода имеют соответственно вид (11.73) и (11.74), в которых требуется вычислить матрицу из решения матричного уравнения Сильвестра (11.67) и матричную показательную функцию

Для решения уравнения Сильвестра (11.67) с матричными компонентами вида (11.83), (11.84) запишем его в столбцовой форме

(11.85)

Выделим в (11.85) по два соседних столбца с индексами в составе каждой из правых матриц. Тогда с учетом структуры (11.83), (11.84) матрицидля смежных столбцовматрицыполучим два уравнения Сильвестра

(11.86)

Решение системы (11.86) относительно фрагмента матрицы , составленного из двух смежных столбцов принимает вид

(11.87)

Матрица как решение матричного уравнения Сильвестра (11.67) в итоге принимает вид

(11.88)

Отметим, что результат (11.88) получен для разночастотного случая дискретных гармонических экзогенных воздействий на входы дискретной динамической системы (11.2) МВМВ- типа, если же режим воздействия одночастотный так, что , то матрицапринимает вид

. (11.89)

Теперь вычислим показательную матричную функцию. Для источникаразночастотного дискретного гармонического воздействия в силу (10.28) путем замены в нем и представленияполучим

. (11.90)

В итоге для векторов состояния , выходаи ошибкивустановившемся режиме для разночастотного дискретного гармонического воздействия можно записать

, (11.91)

где принимает вид (11.88), а- (12.90) Завершая рассмотрение проблемы конструирования аналитического представления реакции динамическойдискретной системы (11.2) в общем случае МВМВ – типа следует заметить, что матрицы ,ивыполняют функциипередаточных матриц (функций) для случая вещественного гармонического экзогенного воздействия.

Как будет показано в разделе 13 книги, глобальная скаляризация векторных процессов в системах МВМВ-типа строится с помощью мажорант и минорант, являющихся для максимальным и минимальным сингулярными числами передаточных матриц,и.

Решение вариантов задач

Задача 11.1. Требуется найти реакцию непрерывной динамической системы в виде переходных функций и по состоянию и выходу:

с передаточной функцией наединичное скачкообразное экзогенное воздействие

Решение.

1. Построение - представления исследуемой ДС осуществим в соответствии с алгоритмом 8.1, для чего передаточную функцию запишем по отрицательным степеням

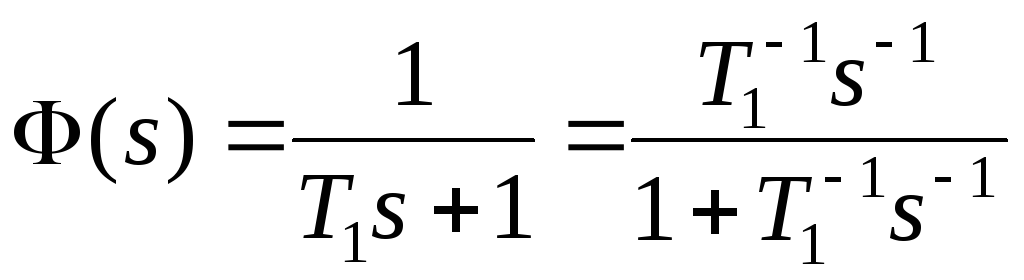, что позволяет для матричных компонентов ВМО (11.1) записать: ;

2. Формирование переходных функций исследуемой ДС по состоянию и выходу с использованием (11.52) дает решение задачи в виде

■

Задача 11.2. Требуется найти реакцию непрерывной динамической системы в установившемся режиме по состоянию и выходу:

с передаточной функцией нагармоническое экзогенное воздействие

Решение.

1. Построение - представления исследуемой ДС в силу решения задачи 11.1 дает матрицы,,;

2. Подстановка полученных матриц в (11.61) с учетом, что , дает решение задачи в форме

. ■