37. Производная функций, заданных параметрически.

{x=x(t)

{y=y(t)

] x(t),y(t) – дифференцируемы.

y`<sub>x</sub>=dy/dx=(y`_t*dt)/(x`<sub>t</sub>*dt)=y`_t/x`<sub>t</sub> (x`(t)≠0)

y`<sub>x</sub>`_x=dy`<sub>x</sub>/dx=((y`_x)`<sub>t</sub>*dt)/x<sub>t</sub>*dt=(y`_x)`<sub>t</sub>/x`_t

38. Теорема Роля, ее геометрический смысл. Замечания.

Если f(x) непрерывна на промежутке a и b [a,b] и в каждой точке интервал a и b, существует производная кроме того, f(a)=f(b), тогда между a и b найдётся одна (ю) с, где f(c)=0

Доказательство:

f(x) – непрерывная на [a,b], имеет min и max.

] m(min)=M(max)=> f(x)=c=>f`(x)=0 на [a,b]

]m<M Ҙ1) x1;x2 f(x1)=m, f(x2)=M

]a<x<b=>f(x1+Δx)>f(x1)=>(f(x1+Δx)-f(x1))/Δx≥0 при Δx>0

lim_Δx->0+0Δf(x)/Δx= lim_Δx->0-0Δf(x)/Δx=0

a<x2<b- аналогично

В точке c касательная к графику функции | y=1-|x|

параллельна оси абсцисс. | f(-1)=f(1)=0 x0=0

Замечания:

lim_Δx->0+0Δf(x)/Δx=lim_Δx->0-0Δf(x)/Δx=0

] x2 принадлежит [a,b] – аналог.

39. Теорема Лагранжа, её геометрический смысл. Формулы Лагранжа.

y=f(x)- непрерывна на замкнутом [a,b] и дифференцируема на (a,b), то (a<c<b), то внутри [a,b] найдётся c в которой равенство – f(b)-f(a)=f(c)(b-a)

Доказательство:

Ф(x)=(f(x)-f(a))

(b-a)=(f(b)-f(a))(x-a)

Ф(x) – непрерывна на [a,b], Ф(a)=Ф(b)=0=>Th Ролля Ҙ (ю) с Ф(с)=0

Ф`(x)=f`(x)(b-a)-(f(b)-f(a))

Ф`(c)=f`©(b-a)-(f(b)-f(a))=0=>f(b)-f(a)=f`(c)(b-a)

b=x+Δx, a=x=>c=x+Ө*Δx(0< Ө<1)

f(x-Δx)-f(x)=f`(x+Өx)Δx 0< Ө<1

Геометрический смысл:

В точке x=c касательная к y=f(x) параллельна хорде стягивающей дуге AB.

40. Теорема Коши (формулировка). Правило Лопиталя.

Th. Коши: Если на [a,b] функции ϕ(x) и ψ(x) непрерывны и дифференцируемы в каждой точке [a,b], ψ(x)≠0 не в одной (.) [a,b], то тогда между точками a и b существует такая (.) c, что имеет место равенство:

Правило Лопиталя: Если функции ϕ(x) и ψ(х) дифференцируемы в окрестности точки а, предел ψ(x) и ϕ(x) при х->a =0 и ψ’(x)≠0, то lim(x->a) ψ(x)/ϕ(x)=lim(x->a) ψ’(x)/ϕ’(x)

41. Формула Тейлора, её вывод.

Y=f(x) [a,b] дифференцируема n раз, то

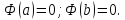
42. Остаточный член в форме Лагранжа

43. Оценка точности Линеаризации.

Абсолютная погрешность:

Относительная погрешность:

44. Представление e^x формулой Маклорена.

...

45. Представление Sin x и Cos x формулой Маклорена.

y= sinx	a=0 y(n)=cos(x+n*п/2) y(n)*c=cos(c+n+п/2) cosx=1-x^2/2!+x^4/4!+…+(cos(n-1)П/2)/(n-1)!)*xn-1+ ((cos(c+n+п/2))/n!)*xn
y=sinx	y(0)=0
y’=cosx	y’(0)=1
y’’=-sinx	y’’(0)=0
y’’’=-cosx	y’’’(0)=-1
yIV=sinx	yIV (0)=0
yV=cosx	yV (0)=1

y= cosx	a=0 y(n)=cos(x+n*п/2) y(n)*c=cos(c+n+п/2) cosx=1-x^2/2!+x^4/4!+…+(cos(n-1)П/2)/(n-1)!)*xn-1+ ((cos(c+n+п/2))/n!)*xn
y=cosx	y(0)=1
y’=sinx	y’(0)=0
y’’=-cosx	y’’(0)=-1
y’’’=sinx	y’’’(0)=0
yIV=cosx	yIV (0)=1
yV=-sinx	yV (0)=0

46. Представление (1+x)^a формулой Маклорена.

a- любое число; х≠-1

y(x)=(1+x) α	y(0)=1 (1+x)=1+∑∞n=1(α(α-1)(α-2)…( (α-1)(α-n+1)/n!)*xn
y’(x)=α(1+x) α -1	y’(0)= α
y’’(x)= α (α-1) (1+x)a-2	y’’(0)= α(α-1)
y’’’(x)= α (α-1)(α-2)(1+x)a-3	y’’’(0)= α(α-1) (α-2)