24. Свойства функций, непрерывных в отрезке.

1-ая теорема Вейерштрасса: если функция непрерывна на замкнутом промежутке AB, то она на нем и ограничена.

2-ая теорема Вейерштрасса: если функция непрерывна на замкнутом промежутке AB, то среди ее значений на этом промежутке имеется наибольшее и наименьшее.

1-ая теорема Больцано-Каши: если функция непрерывна на замкнутом промежутке AB и на его концах принимает значения разных знаков, то на этом промежутке найдется хотя бы 1 точка, в которой функция ровна нулю.

2-ая теорема Больцано-Каши: если функция непрерывна на замкнутом промежутке AB, то, принимая любые два значения на AB, она принимает и любое промежуточное значение.

25. Задачи о касательной и мгновенной скорости.

V=S/t=ΔS/Δt

V=lim_Δt->0ΔS/Δt=S`(t)

Δx=>N->M

lim_Δx->0Δy/Δx=tgα

Δy/Δx=tgβ

26. Определение производнойб её геометрический смысл.

Опр1: Производной функции y=f(x) в точке x называется предел отношения приращения функции к вызывавшему его приращению аргумента при условии, что последнее стремиться к нулю.

y`_x(x)=lim_Δx->0Δy/Δx= lim_Δx->0 (y(x+Δx)-y(x))/ Δx

Геометрический смысл производной: Значение производной в точке равно tg в углах направленный к касательгой проведённой к графику функции в этой точке.

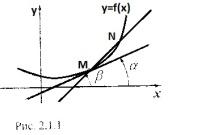
Геометрический смысл. tgβ=Δy/Δx tgα=lim(Δx->0)Δy/Δx=y'x(x)

27. Необходимое и достаточное условие дифференцируемости.

Для того чтобы функция y=f(x), была дифференцируема в точке  что бы полное приращение в точке x, соответсявющее приращению Δx, можно было представить в виде Δy= A*Δx+α(Δx)* Δx

Доказательство:

α(Δx)->0 при Δx->0

Y – дифф. Если Ҙy_x=lim_Δx->0Δy/Δx=>Δy/Δx-y`<sub>x</sub>=α=> ]α=α(Δx) Δy=y`_x*Δx+α(Δx)* Δx A=y`_x<=Δ=a*Δx+α(Δx)* Δx |:Δx

Δy/Δx=A+α(Δx)=> lim_Δx->0Δy/Δx=a+> y=y`_x

28. Основные правила дифференцирования(с доказательством).

Производная постоянной

Y=c (c-Const)

C`_x= lim_Δx->0Δy/Δx= lim_Δx->0c-c/Δx=0

Правила дифференцирования:

1. (с*f(x))`=c*(f(x))` c-Const

2. (f(x)±g(x))`=f`(x)±g`(x)

3. (f*g)`=f`(x)*g+f*g`(x)

4. (f(x)/g(x))`=(f`(x)*g-f*g`(x))/g²(x)

(f(x)/g(x))`= lim<sub>Δx->0</sub>(U(x+Δx)/V(x+Δx))-(f(x)/g(x))= lim<sub>Δx->0</sub>(U(x+Δx)*V(x)- U(x)*V(x+Δx))/ Δx* U(x+Δx)*V(x)= lim<sub>Δx->0</sub>((U(x+Δx)*V(x)- U(x)*V(x+Δx))/ Δx* U(x+Δx)*V(x))* *U(x+Δx)*V(x))= lim<sub>Δx->0</sub> (V(x)U`(x)-U(x)V`(x))/V²(x)

29. Правило дифференцирования сложной функции(правило цепочки).

30. Производная степенной и показательной функций.

1. y=x^α (α ϵR) – смешанная функция

(x^α)`_x= lim_Δx->0Δy/Δx= lim_Δx->0((x+Δx)^α-x^α)/Δx= lim_Δx->0(x^α(1+Δx/x)^α-x^α)/Δx= lim_Δx->0(x^α*α*Δx/x)/Δx=αx^α-1

2. Показательная функция.

Y=a^x (a>0,a≠1)

(a^x)`= lim_Δx->0(a^x+Δx-a^x)/Δx= lim_Δx->0(a^x+Δx-a^x)/Δx= lim_Δx->0a^x(a^Δx-1)/Δx= lim_Δx->0a^xlna*Δx/Δx=a^x*lna

31. Призводные тригонометрических функций.

1. y=Sin(x)

(Sinx)`= lim_Δx->0(Sin(x+Δx)-Sinx)/Δx= lim_Δx->0(Sinx*CosΔx+Cosx*SinΔx-Sinx)/Δx= lim_Δx->0(Sin(CosΔx-1)+Cosx*SinΔx)/Δx= lim_Δx->0(-Sin2Sin²Δx/2)/Δx+(CosxSinΔx)/Δx= lim_Δx->0(-Sin*Δx²/2)Δx+Cosx=Cosx

1. y=Cosx

(Cosx)`= lim_Δx->0((Cos(x+Δx)-Cosx)/Δx= lim_Δx->0 (Cosx*CosΔx-Sinx*SinΔx)-Cosx)/Δx= lim_Δx->0 (Cosx(CosΔx-1)-Sinx*SinΔx)/Δx= lim_Δx->0 (Cosx*(Δx²/2))/(Δx)-Sinx=-Sinx

2. (tgx)`=(Sinx/Cosx)`= lim_Δx->0 (Cosx*Cosx-Sinx*(-Sinx))/Cos²x= lim_Δx->0 (Cos²x+Sin²x)/Cos²x=1/Cos²x

3. (ctgx)`=-1/Sin²x

32. Производная обратной функции. Производная логарифма.

y=log_ax (a>0,a≠1)

y`_x= lim_Δx->0(Log_a(x+Δx)-log_ax)/Δx= lim_Δx->0(log_ax(1+Δx/x)-log_ax)/Δx= lim_Δx->0(log_ax+loga(x+Δx/x)-log_ax)/Δx= lim_Δx->0(1/lna*Δx/x)/Δx=1/(x*lna)

(lnx)`=1/x

33. Производная обратной функции. Производная арксинуса.

y=arcSinx=>x=Siny

y`(x)=1/x`_y=(1/(Siny)`)=(1/Cosy)=1/(sqrt(1-Sin²y))=1/(sqrt(1-x²))

(arcSinx)`=1/(sqrt(1-x²))

arcSinx+arcCosx=П/2

(arcCosx)`=(П/2-arcSinx)=-1(sqrt(1-x²))

34. Производная обратной функции. Производная арктангенс.

(arctgx)`=1/(tgy)`=1/1/Cos²y=1/(1+tg²y)=1/(1+x²)

(arcctgx)`=-1/(1+x²)

35. Дифференциал:3 определения, инвалентность.

Опр1: Линейная относительная Δx часть приращения дифференцируемой функции y=f(x) называется дифференциалом этой функции и обозначается dy, т.е. dy=^defy`_x*Δx

Инвалентность:

dy=y`_x*dx

] {x=x(t)

{y=y(t) y=y(x)

dy=y`<sub>t</sub>*dt=y`_x*x_t*dt=y`_x*dx

36. Применение дифференциала к приближенным вычислениям. Линеаризация.

Δy=f(x-Δx)-f(x)

Δy=f`(x)Δx+α(Δx)Δ=>f(x+Δx)=f(x)-f(Δx)Δx+α(Δx)Δx

f(x+Δx)≈f(x)+f`(x)Δx

Пример1: Плоский металлический диск R=1м, после нагрева увеличился на 1 см, вычислить S после нагрева.

S(R)=2ПR²

S(R+ΔR)=П(R+ΔR)²

S+ΔS=П(1+0,01)²=П(1+0,02+0,0001)=П*1,0201м²

S`(R)=2пR

S±(R+ΔR)=S(R)+S`(R)*ΔR=П+2П*0,01=1,02*Пм²

|ΔS-dS|=|0,0201П-0,02П|=0.0001м²

|(ΔS-dS)/ΔS|=0,02=2%

Линеаризация - замена приращения Δf функц. в (.)х для малых приращений Δх ее дифференциалом, мы, тем самым, на участке от х до х+Δх заменяем функцию ленейн функц.