Общее выражение

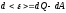- соответствует первому началу термодинамики по типу dA

Связав во 2-ом способе изменение энергии системы (по типу dA) с изменением её внешних координат (объём, поверхность, потенциальное силовое поле и т.д.), а также силами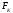, связанными с этими изменениями по соотношению:

где

- среднее значение силы

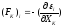- её (вероятностные силы) составляющие, связанные с изменением 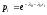состояния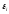частиц системы при изменении координат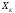, но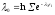сохранении распределения вероятностей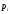как и в равновесном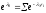состоянии, т.е. при обратимом протекании процессов совершения работы(без трения)

Тогда

Так как 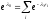, то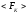можно записать в виде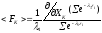

или 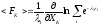, которое согласно уравнению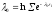приводится к легко запоминающейся форме:

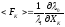
Статическая “средняя” сила в макросистеме идеального газа. Статическое вычисление силы давления и вывод уравнения состояния

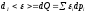- по первому способу

Итак, рассматривая 2-ой способ изменения энергии системы через совершение работы dA: (при сохранении распределения вероятностейи изменении уровней) с изменением её внешних координат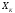(объёма, поверхности, потенциального силового поля и т.п.) и действующей «средней» статической силой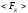, т.е.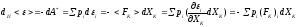

где 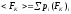- среднее значение (мат.ожидание) действующей силы

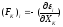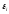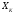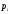- вероятностные составляющие этой силы, связанные с изменением уровней энергии системы при изменении её внешней координаты, но при сохранении распределения вероятностейкак и в равновесном состоянии, т.е. при протекании обратимых процессов совершения работы

Поскольку как было показано ранее

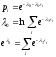
то для средней силы можно записать ,

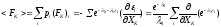Так как 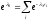, то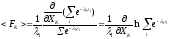

С учетом равенства 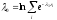,, получим легко запоминающуюся форму для “средней” действующей силы;,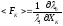

Теперь, рассматривая давление Р в системе идеального газа как среднюю статическую силу, связанную с изменением его объёма V, получим:

,

где согласно прежним вычислениям 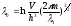- для одной частицы или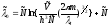- для 1-го моля частиц с числом частиц -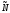

Последнее выражение получено исходя из аддитивности энтропии:

- для 1-ой частицы, где

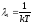
и

- для 1-го моля частиц с числом частиц - 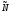, где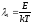

Если рассматривать систему из неразличимых частиц, то полная неопределенность 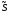включает в себя такую величину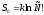возникающую в следствии того, что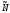неразличимых частиц могут быть представлены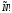способами, т.е. состояния, которые отличаются друг от друга только заменой тождественных частиц на самом деле неотличимы друг от друга и должны считаться одним состоянием. Следовательно, для системы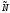тождественных различимых частиц. Неопределенность части суммы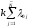будет меньше чем в случае неотличимых частиц, т.е. должна быть уменьшена на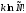, т.к. эта поправка не сказывается на энергии. В результате получим:

, где

Тогда для 1-го моля частиц :

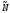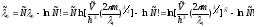
Используя формулу Стирлинга для 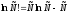, получим

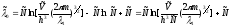
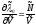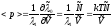Отсюда нужная нам производная , и следовательнос учетом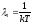

Так как для 1-го моля вещества 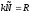(универсальная газовая постоянная), то в итоге получаемуравнение состояния идеального газа в статическом виде:

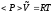
Полученное статическое распределение частиц по энергиям позволяет рассчитать среднее изменение количества движения частиц при их упругом взаимодействии со стенкой, образующей газовый объём V, т.е. рассчитать то, что называется давлением газа.

Для этого вернемся к взаимосвязи энергии и импульса (ограничиваясь движением в одном направлении i, перпендикулярном стенке)

,

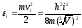причем вероятность обладания этой скоростью 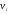составляет

,

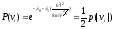Где учтено, что частица может двигаться либо вправо, либо влево при одной и той же абсолютной скорости .

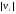Так как за промежуток времени частицы находящиеся на расстоянии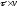от стенки и имеющие скоростьпо направлению, перпендикулярном к ней, при ударе о неё передающей свой импульс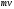и отскакивают от неё с той же энергией (той же абсолютной скоростью), тополное изменение количества движения в расчете на одну частицу будет равно 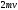, а в расчете на все частицы, находящие в объёме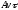, гдеA –площадь стенки, при их средней плотности 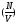в ограждённом стенкой газовом объёмеV, составляет:

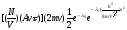
Так как давление есть сила, равная изменению количества движения на единицу площади стенки в единицу времени, то поделив предыдущее выражение на и просуммировав его по всемi, получим:

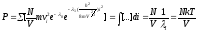
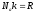Для одного моля вещества произведениеи в итоге получим:

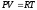- уравнение состояния идеального газа

Для одной частицы (на ящик приходится одна частица):

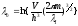
Математическое ожидание энергии:

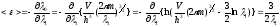
“Острота” распределения вероятностей задается дисперсией:

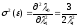
Относительное отклонение (для одной частицы) будет равно:

,

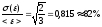т.е. хотя вероятность выпадения герба при бросании монеты равна , предсказание для одного броска довольно часто может быть ошибочным.

Для N частиц средняя энергия равна энергии одной частицы умноженной на N:

(здесь использована аппроксимация Стирлинга )

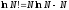Дисперсия для N частиц:

Относительное отклонение для N~6*10²³ (одного моля вещества):

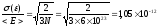
Рассмотрим в общем виде изменении энтропии:

, где ,,

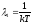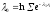
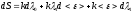
Так как по первому закону термодинамики:

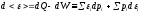
где 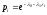;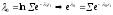зависит только от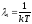(для первого способа изменения энергии), а также от внешних условий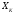(деформации координаты, объёма, поверхности, под действием внешней силы(силового поля) для второго способа изменения энергии), то в общем случае можно записать:

,

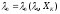т.е.

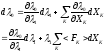
где - обозначено некоторое значение силы

Тогда для общего изменения энтропии получим:

- второе начало термодинамики, где ,,

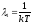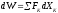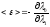
Константу K, которая в своё время была введена как произвольная постоянная в неопределенности S положим равной постоянной Больцмана K=k, тогда получаем второй закон термодинамики:

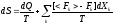
- физическая энтропия, связанной с (теплообменом) передачей теплоты dQ и производством работы dA при температуре системы T.

Это выражение позволяет физически оценить меру неопределенности информационной энтропии, с помощью измерения некоторых физических параметров

Есть ещё одна интересная интерпретация энтропии как меры неопределенности, известная как третий закон термодинамики

Как следует из информационного определения энтропии: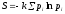

при условиях:

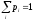
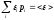
вероятность 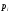являются функцией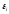иT, т.е. 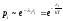(без переноса частиц вещества т.е. учитывая)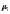

Рассмотрим отношение вероятностей двух состояний с энергиям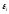и и: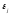

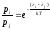
и проанализируем, что происходит с газом при уменьшении 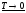(т.н. вырожденный газ):

,

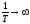, если

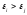
т.е. если температура падает, то только самые нижние энергетические уровни имеют заметную вероятность быть занятыми.

Обозначив минимальный уровень энергии 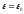, и соответствующую этому состоянию вероятность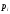(остальные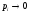для всех энергетических уровней)

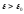Если вероятности этих X самых энергетически низких состояний равны, тогда - число такихi:

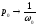
Тогда можно записать:

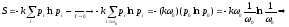
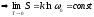- теорема Нернста (третье начало термодинамики)

Это соотношение определяет важную связь между физической энтропией и вероятность наиболее предпочтительного энергетического состояния, указанную Больцманом и увековеченную на его могильной плите.

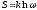, - число состояний

Это утверждение 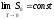при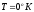известно кактеорема Нернста, согласно которой энтропия газа при T=0 K является величиной постоянной.

Распределение частиц при 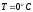на низких энергетических уровнях в статистиках Бозе-Эйнштейна и Ферми-Дирака показаны на рис., где для определения принято что все

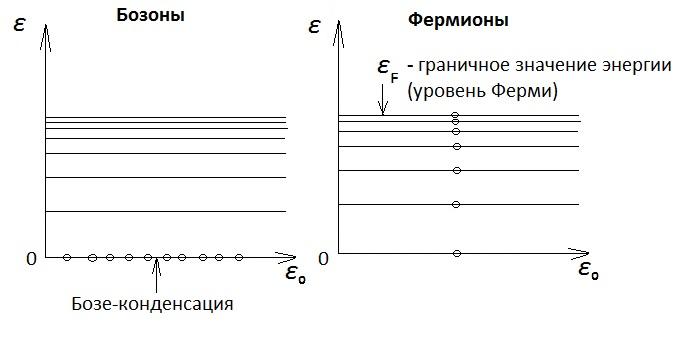
Ферми совпадает с предельным значением химического потенциала

Последнюю картинку для фермионов можно представить (изобразить) и в другом виде. В виде ступенек, отражающие зависимость числа частиц 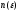приT=0

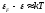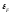Если несколько повысить температуру, то тепловая энергия будет сообщаться вначале только частицам, имеющим энергию близкую к. Поэтому на более высокий уровень могут перейти только такие частицы, для которых разность соседних уровней. Частицы, расположенные на более глубоких уровнях, не изменят своего состояния. Таким образом с повышением температуры происходит “размывание” уровня Ферми, и эта зона размыва имеет ширину порядка.