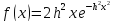2.5 Функция распределения и плотность распределения случайной величины

Характеристикой случайной величины служит вероятность появления различных её значений. Для их задания используется функция распределения случайной величины, обозначающая последовательное расположение возможных значений случайной величины и отвечающих им вероятностей.

F (x) = P (X<x),

Где P (X<x) - вероятность выполнения неравенства Х<х, которая рассматривается как функция переменной х.

Если Х - дискретная случайная величина, возможные значения которой пронумерованы в порядке их возрастания x₁, x₂ ,…, x_n, a вероятности этих значений соответственно равны p₁, p₂,…,p_n, то функция распределения определяется формулой:

F (x) =

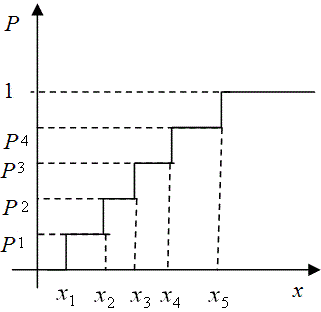
Эта функция изменяется ступенчато. Для непрерывной случайной величины функция распределения непрерывна.

Производная от функции распределения случайной величины называется плотностью распределения вероятности:

f (x) = F’ (x)

В свою очередь, функция распределения выражается через плотность распределения по интегральной формуле:

F (x) =.

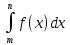2.6 Математическое ожидание случайной величины

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее значений на вероятности этих значений:

М[x]=M_x=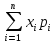

Для непрерывной случайной величины математическое ожидание выражается интегралом

М[x]=M_x=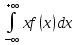

В случае равной вероятности появления случайной величины в n опытах, где 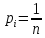, математическое ожидание может трактоваться как среднее значение случайной величины

М[x]=M_x=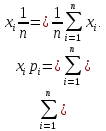

2.7 Дисперсия случайной величины

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания

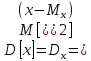
Для дискретной случайной величины

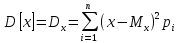
Для непрерывной случайной величины

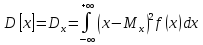
Положительный корень из дисперсии называется средним квадратным отклонением случайной величины

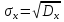
2.8 Законы распределения вероятностей случайных событий и случайных величин

Одной из самых простых исторически первых формул является выведенное во второй половине XVII века Якобом Бернулли, так называемое, биномиальное распределение.

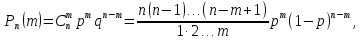
Где 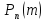характеризует вероятность появления ровно m раз события А из серии n опытов, в каждом из которых событие А появляется с одинаковой вероятностью р или не появляется с вероятностью 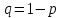;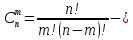число сочетаний изn элементов по m (бином Ньютона ).

При большом числе опыте и редком появлении событий вычисление факториалов (n-m+1)! и m! в формуле Бернулли становится слишком громоздкими и на практике используется приближенная формула распределения Пуассона:

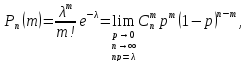
где λ=const– среднее число появлений события А в серии n.

В качестве домашнего задания выполните переход от биномиального распределения к распределению Пуассона.

Если рассматривается вероятность появления редких событий на заданном промежутке времени t и средним числом λt, то

λ =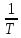– интенсивность событий, т.е. среднее число событий в единицу времени.

Предположим, что необходимо определить время безотказной работы R прибора. Для этого примем m=0 на интервале времени t:

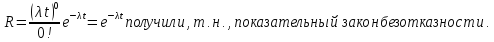
Тогда вероятность отказа как противоположного события будет равна:

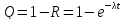
Потоки событий, распределение вероятности, которых подчиняется закону Пуассона, обладают свойствами:

• ординарность - когда вероятность одновременного появления двух и более событий равна нулю;

• отсутствие последствий - когда вероятность не зависит от момента совершения предыдущих событий;

• стационарность - когда вероятность попадания того или иного числа событий на участок времени, зависит только от длины этого участка.

При неограниченном возрастании числа наблюдений () распределение Бернулли, согласно центральной предельной теореме Муавра-Лапласа, приближается к т.н. нормальному распределению Гаусса.

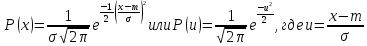
u – безразмерная функция отклонения непрерывной случайной величины х от ее математического ожидания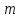(центра нормализованного распределения) с дисперсией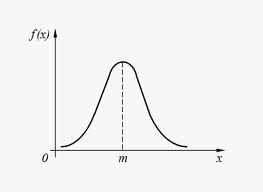

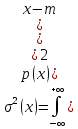
На практике часто применяются различные модификации этих законов распределения:

• распределение Вейбулла

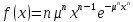
• гамма-распределение

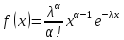
• распределение Пирсона

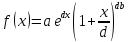
• распределение Релея