Распределение Бозе-Эйнштейна

Обозначим через W, число различных способов, которыми можно разместить N, частиц в r_i ячеек. Так как частицы в квантовом случае считаются неразличимыми, то эти способы могут отличаться друг от друга только числом частиц в ячейках, при фиксированном числе частиц в ящике N_i . Разные способы отличаются друг из друга путем переноса частиц из ячейки в ячейку (обменом местами частиц и перегородок).

Зафиксировав каждое такое распределение, оценим всевозможные несущественные (т.е. не дающие новых способов распределения) перестановки частиц друг с другом (их число равно N_i!) и перегородок друг с другом (их число при r, ячеек равно (r_i-1)!)

Очевидно, что все число перестановок из всех этих (N_i +г_i-1) объектов, включающих и частицы и перегородки.

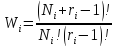
Если мы имеем ряд ящиков, то число способов W распределения частиц по всем ящикам будет равно

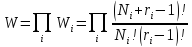
Максимум величины W, т.е. наиболее вероятное распределение, при наложенных условиях:

Задано полное число частиц

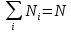
Задана полная энергия

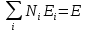
Находиться уже известным нам методом неопределенных множителей Лагранжа для функции:

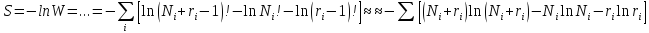
где использована формула Стирлинга для факториалов больших чисел N> 1 и г_i>>1 при больших значениях N последнее слагаемое мало по сравнению с каждым из первых двух (уже для N=10³ оно составляет около 0,4%).

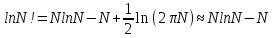
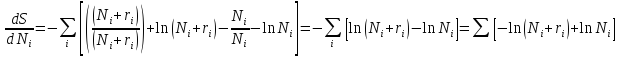
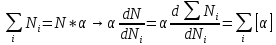
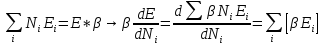
В соответствии с методом неопределенных множителей Лагранжа, приравняем нулю производную.

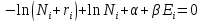
или

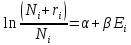
Где α и β множители Лагранжа

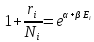
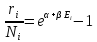
отсюда для наиболее вероятного числа частиц в ячейке имеем распределение Бозе-Эйнщтейна (1924)

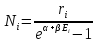
Где α и β определяются условием

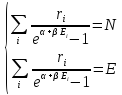
которые дают уже известные нам значения

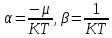
Распределение Ферми - Дирака

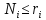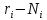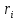Если учесть принцип запрета Паули, то в каждой ячейке одного ящика не может быть больше одной частицы, т.е. . Поскольку при этом частицы неразличимы, то различные способы их размещения по ячейкам в ящике различаются только тем, какие ячейки заняты одной частицей, а какие свободны, или иначе говоря, перестановками пустых ячееки занятых, ячеек между собой т.е. перестановкой всех, ячеек:

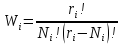
Общее число способов распределения N частиц по всем ящикам при условии, что в i-й ящик попадает N, частиц, равно произведению

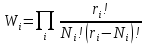
Максимум величины W, дающей наиболее вероятное распределение при условиях

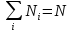
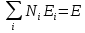
Находится как и прежде методом неопределенных множителей Лагранжа:

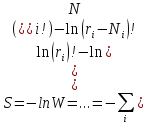
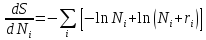
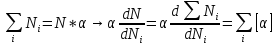
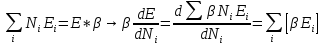
приравниванием нулю производную

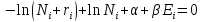
Откуда для чисел заполнения N_i в ячейках получаем распределение Ферми - Дирака

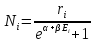
где α и β определяются из условий:

которые дают уже известные нам значения:

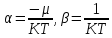
Это выражение отличается от полученного ранее распределения Бозе- Эйнштейна только знаком перед единицей в знаменателе:

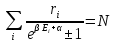
Если при любых Е_i, выполняются условия разряженности (N/V) газа 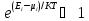, то оба эти квантовые распределения переходят (при больших массах и высоких температурах) в Больцмана - Максвелла.

Статистическая термодинамика

Вывод уравнений феноменологической термодинамики на основе полученных статистических соотношений для системы из N частиц, находящихся в i-тых состояниях с вероятностью p_i:

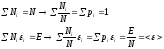
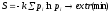
Вероятность p_i находится на основе минимизации 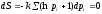информационной энтропии Шеннона методом Джейнса сиспользованием неопределенных множителей Лагранжа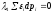для дополнительных условий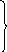

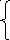
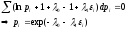
где 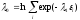из (1)

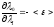из (2),

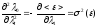
Тогда

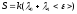
Рассмотрим в общем виде изменение математического ожидания (среднего значения) энергии <>

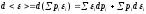
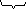
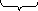
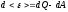(другое общепринятое обозначение работы dW)

Здесь 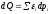- представляет собой такой способ изменения энергии, при котором изменяются вероятности распределения её уровней при сохранении их значений

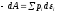- наоборот, сохраняет распределение вероятностей при изменении уровней энергии

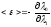Для осуществления 1-го способа изменения энергии (по типу dQ) можно объединить две системы с различными значениями , это из соотношеният.е. для данного набора значений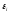средняя энергия зависит только от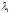, причем т.к.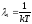то увеличение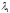(при постоянных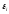) обозначает уменьшение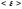, а так как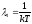, то при объединении двух систем с разными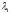средняя энергия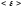в одной системе будет уменьшаться (где меньше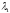, т.е. больше температураT), а в другой – увеличиваться за счет эффекта нагревания. Такой способ изменения энергии называется передачей теплоты (теплообменом) до тех пор, пока значения 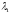не сравняются, т.е. пока не наступит тепловое равновесие.

Для осуществления 2-го способа изменения энергии (по типу dA) можно изменить внешние условия системы (например, её объём V с помощью некоторого поршня, давящего на систему, т.е. изменяющего координаты 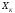её частиц – их потенциальную энергию). Этот способ изменения энергии называетсяработой.