1.6.2. Элементы теории множеств

Множеством называется любое объединение определенных вполне различимых объектов; их может и не быть вообще. Можно говорить о множестве точек на отрезке [0,1], множестве студентов в группе, множестве снежных дней в июле на экваторе, т.е. множество образуют любые объекты, объединенные по любому признаку. Объекты, составляющие множество, называются элементами множества. Множество, не имеющее ни одного элемента, называется пустым, оно обозначается . Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным.

Задать множество можно перечислением его элементов. Например, множество образованное из n элементов a1,a2,…,an , обозначается A={ a1,a2,…,an }; пишется aA (говорится «элемент a принадлежит множеству A»), если a является элементом множества А, в противном случае aA.

Задать множество можно также, указав общее свойство для всех его и только его элементов. Например, множество точек равноудаленных от концов отрезка.

Два множества считаются равными, если состоят из одних и тех же элементов; записывается этот фактA=B.

Множество А₁называетсяподмножествомА(записываетсяА₁А), если все элементы множестваА₁являются элементамиА.

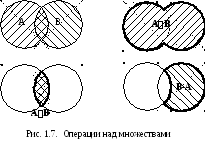
Для множеств определены следующие операции: объединения, пересечения, дополнения.

Объединением множествАиВ (записываетсяAB) называется множество состоящее из элементов как одного так и второго множества. Например,A иB – множества точек принадлежащих некоторым двум кругам, имеющим общие точки, тогда объединениемAB будет фигура, состоящая из общих точек.

Пересечением множествАиВ (записываетсяAB) называется множество, состоящее из элементов, принадлежащих как одному так и второму множеству одновременно.

Дополнением множества АдоВ называется множество, состоящее из элементов множестваВ,не принадлежащихА. Дополнение обозначаетсяĀ=В-А.

1.6.3. Элементы теории графов Основные понятия

Г

.

рафзадается парой множеств: множества E называемогомножеством вершини множестваU,называемогомножеством ребер. РеброuU есть пара (e_i,e_j), гдеe_i,e_jE, указывающая, между какими двумя вершинами проведено ребро. Говорят, что реброuUинцидентновершинамe_i,e_j. Если порядок ребер не имеет значения, т.е.

u=(e_i,e_j)=(e_j,e_i), то ребро называетсянеориентированнымили просто ребром, если же порядок имеет значение, то реброu=(e_i,e_j) называетсяориентированным ребромилидугой. Вершинаe_i - называетсяначалом дуги,e_j–конец дуги. Граф, содержащий хотя бы одну дугу, называетсяориентированным графом илиорграфом.

Граф G(E,U)называетсяконечным, если множество Eвершин конечно.

Граф G(E,U), у которого любые две вершины соединены ребром, называетсяполным. Если хотя бы две вершины соединены несколькими ребрами, то такой граф называетсямультиграфом. Две вершиныe_i,e_jEназываютсясмежными, если они соединены ребром. Число ребер, инцидентных данной вершинеe_i, называетсялокальной степеньюэтой вершины(e_i). Число реберr графаG(E,U) определяется выражением

, гдеn – количество вершин в графе.

Рассмотрим граф, изображенный на рисунке 1.8.

Ориентированный граф рис. 1.8.

Множество вершин графа состоит из пяти элементов E={1,2,3,4,5}, а множество реберU={(1,2),(1,4),(1,5),(2,3),(3,4),(5,3)}. Ребро (5,3) – является ориентированным ребром или дугой. Число ребер в графе определяется по значению локальных степеней для каждой вершины:

(1)=3; (2)=2; (3)=3; (4)=2; (5)=2; r=(3+2+3+2+2)/2=6

Важным в теории графов является понятие части графаG(E,U), который обозначаетсяG(E,U)G(E,U)

Множества вершин и ребер части графа являются подмножествами вершин и реберисходного графа

EE UU

Многие задачи на графах состоят в определении частей графа с заданными свойствами.

Часть графа G(E,U)G(E,U) называетсяподграфомграфаG(E,U), еслиEE, а подмножествоUUобразовано только ребрами инцидентными вершинам множестваE.

Часть графа G(E,U)G(E,U) называетсясуграфомграфаG(E,U), еслиEE, а подмножествоUUобразовано ребрами инцидентными вершинам множестваE. В графе, изображенном выше, можно выделить подграфG(E,U), гдеE={1,2,3},множество реберU={(1,2),(2,3)}и суграфG(E,U), у которогоE={1,2}, U={(1,2),(1,4),(1,5),(2,3)}.

Полнымграфом называется графG(E,U), у которого каждая вершинаe_iE соединена ребрами с остальными вершинами. Например,

Рис. 1.9. Полный граф