7. Потроение леальных кривых и касательных к ним

При сечении прямого кругового конуса плоскостями, расположенными различно по отношению к осям конуса, получаются контуры сечения, образующие эллипс, параболу, гиперболу.

При пересечении плоскостью P_v всех образующих конуса получается эллипс (рис. 10 а,б).

Эллипс – замкнутая плоская кривая, сумма расстояний каждой точки которой до двух данных точек (фокусов), лежащих на большой оси, есть величина постоянная и равная длине большой оси.

Ш

А

В

D

C

О

ироко применяется в технике способ построения эллипса по большой АВ и малой СD осям (рис. 10 в).

Рис. 10. Построение эллипса

Проводят две перпендикулярные осевые линии. Затем от центра О откладывают вверх и вниз по вертикальной оси отрезки, равные длине малой полуоси, а влево и вправо по горизонтальной оси – отрезки, равные длине большой полуоси.

Из центра О радиусами ОА и ОС проводят две концентрические окружности и ряд лучей-диаметров. Из точек пересечения лучей с окружностями проводят линии, параллельные осям эллипса, до взаимного пересечения в точках, принадлежащих эллипсу. Намеченную линию обводят по лекалу.

Точки сопряжения кривых – это точки, в которых сопрягаемые кривые имеют общую касательную. Построение сопряжения кривых в заданных точках сводится к построению касательных в этих точках (рис. 11).

АВ и СD – оси эллипса, точка Р– произвольная точка, через которую проводим касательную. С помощью радиуса R=ОА находим фокусы эллипса точки F₁ и F₂ (СF₁ = СF₂ = R = ОА= ОВ). Соединяем точку Р с фокусами F₁ и F₂. Биссектриса угла F₁РF₂ будет нормалью n, к которой и строится касательная t.

R=OA

PF₁+PF₂=AB

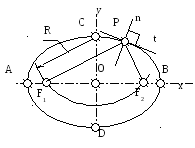
Рис.11. Построение касательной к эллипсу в точке Р:

АВ и СD – оси эллипса, F₁ и F₂ - фокусы

При сечении прямого кругового конуса плоскостью Р, параллельной одной из образующих конуса (рис. 12 а,б), получается парабола.

Парабола – плоская кривая, каждая точка которой равноудалена от директрисы DD₁ – прямой, перпендикулярной к оси симметрии параболы, и от фокуса F – точки, расположенной на оси симметрии параболы (рис. 12 в).

Расстояние КF между директрисой и фокусом называется параметром p параболы. Точка О, лежащая на оси симметрии, называется вершиной параболы и делит параметр p пополам.

Для построения параболы по заданной величине параметра p проводят ось симметрии параболы (на рис. 12 вертикально) и откладывают отрезок КF = p. Через точку К перпендикулярно оси симметрии проводят директрису DD₁. Отрезок КF делят пополам и получают вершину О параболы. От вершины О на оси симметрии отмечают ряд произвольных точек I –VI c постепенно увеличивающимся расстоянием между ними. Через эти точки проводят вспомогательные прямые, перпендикулярные оси. На вспомогательных прямых из фокуса F делают засечки радиусом, равным расстоянию от прямой до директрисы. Например, из точки F на вспомогательной прямой, проходящей через точку V, делают засечку дугой R₁ = KV; полученная точка 5 принадлежит параболе.

а) б) в)

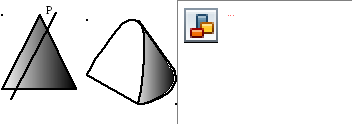
Рис. 12. Построение параболы

Если требуется построить параболу по заданной вершине О, оси ОС и точке В (рис. 13 а), то строят вспомогательный прямоугольник АВСО. Стороны прямоугольника АВ и ОА делят на равные части и точки деления нумеруют. Горизонтальный ряд делений соединяют лучами с вершиной О, а через точки делений, расположенные на АО, проводят прямые линии, параллельные оси параболы. Точки пересечения горизонтальных прямых 1₁, 2₁, 3₁, … с лучами О1, О2, О3, … принадлежат параболе.

В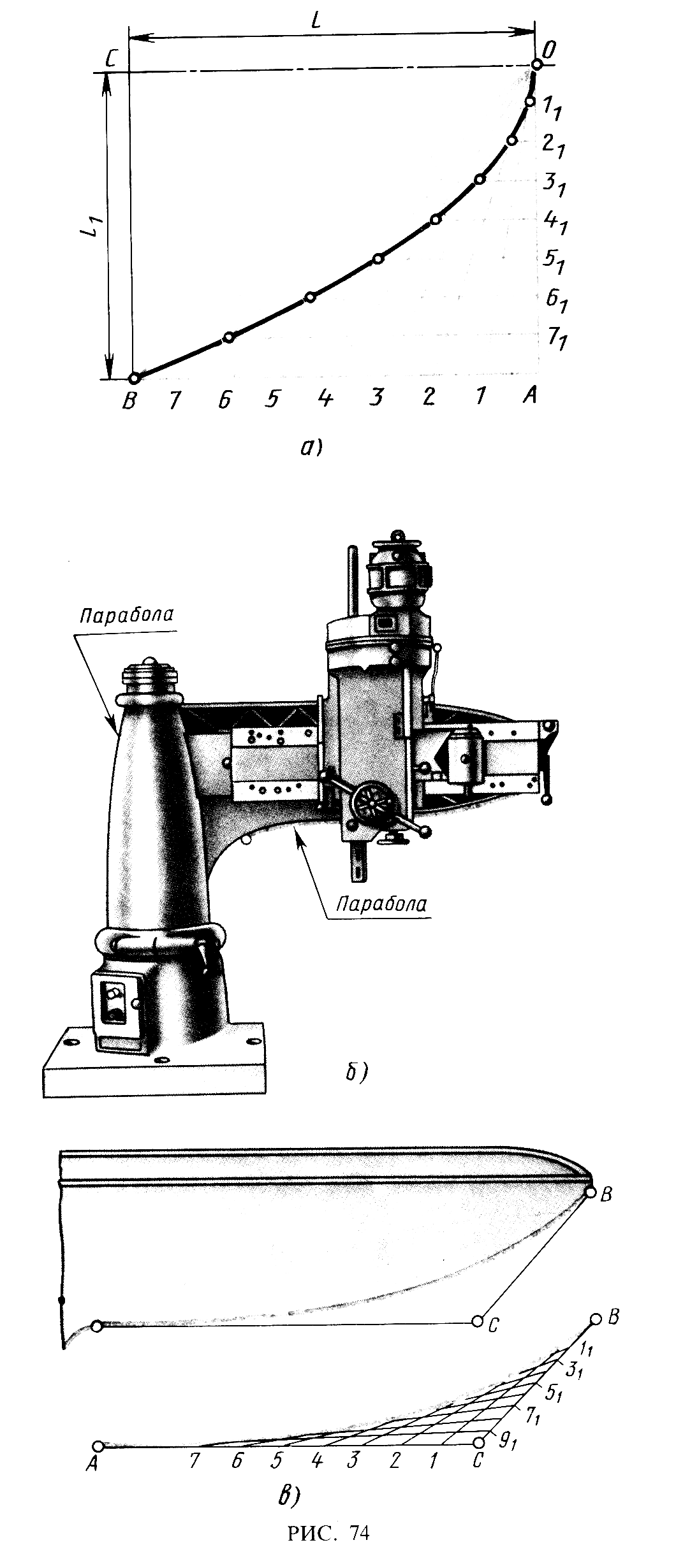 станкостроении и других отраслях машиностроения часто применяются детали, контурные очертания которых выполняются по параболе, например, стойка и рукав радиально–сверлильного станка (рис. 13 б).

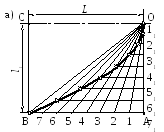
Рис. 13. Применение контурных очертаний, выполненных по параболе

П

y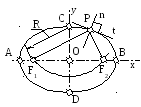

остроение касательной в произвольной точке К параболы показано на рис. 14. Точку К соединяем с фокусом F, прямая ЕК перпендикулярна к директрисе у, ЕК=КF. Биссектриса угла ЕКF и будет касательной к параболе в точке К. Точку К соединяем с фокусом F. Прямая ЕК перпендикулярна к директрисе y.

Рис. 14. Построение касательной к параболе в точке К:

х – ось параболы, у – директриса, А – вершина,

F – фокус

П ри сечении прямого кругового конуса плоскостью Р, параллельной оси конуса (рис. 15 а,б, в), получается гипербола.

Рис. 15. Построение гиперболы

Гипербола – плоская кривая, состоящая из двух разомкнутых, симметрично расположенных ветвей (рис.15 в). Разность расстояний от каждой точки гиперболы до фокусов F и F₁ есть величина постоянная и равная расстоянию между вершинами гиперболы А и В.

Рассмотрим прием построения гиперболы по заданным вершинам А и В и фокусному расстоянию FF₁. Разделив фокусное расстояние FF₁ пополам, получают точку О, от которой по обе стороны откладывают по половине заданного расстояния между вершинами А и В. Вниз от фокуса F намечают ряд произвольных точек 1, 2, 3, 4 … с постепенным увеличением расстояния между ними. Из фокуса F описываем дугу вспомогательной окружности радиусом R, равным, например, расстоянию от вершины гиперболы В до точки 3. Из фокуса F₁ проводят вторую дугу вспомогательной окружности радиусом r , равным расстоянию от вершины А до точки 3.На пересечении этих дуг находят точки С и С₁, принадлежащих гиперболе. Таким же способом находят остальные точки гиперболы. Вторую ветвь гиперболы строят аналогичным образом.

Построение гиперболы по известным ее асимптотам^ l₁ и l ₂ и точке Р показаны на рис. 16 а,б.

Первый способ (рис. 16 а): через точку Р проводятся прямые, параллельные асимптотам l₁ и l₂, находятся точки пересечения произвольных лучей, проведенных из точки О с этими прямыми. Дальнейшие построения на рис. 16а показаны стрелками.

Второй способ построения (рис. 16б) заключается в проведении лучей через точку Р до пересечения с асимптотами.

a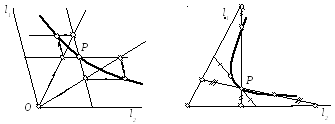) б)

Рис.16. Построение гиперболы по асимптотам l₁ и l₂ и точке Р

Построение касательной в произвольной точке Р гиперболы показано на рис. 17. Точка Р соединяется с фокусами гиперболы F₁ и F₂, далее строится биссектриса угла F₁PF₂, которая и будет касательной к гиперболе в точке Р.

Касательная к гиперболе, построенной по заданной точке и двум асимптотам ^ х и у, в некоторой точке Р строится следующим образом (рис.18). Через точку Р проводится прямая, параллельная одной из асимптот. На другой асимптоте откладывается отрезок 1М=01. Прямая МР является касательной к гиперболе. На рис. 18 показана одна ветвь равнобочной гиперболы (асимптоты перпендикулярны). Построение касательных к другим гиперболам аналогично.

F₁F₂=2c, A₁A₂=2a

F₂P-F₁P=2a

Рис. 18. Построение касательной к

ветви равнобочной гиперболы

в точке Р:

х, у – асимптоты,

ОА – действительная ось,

О – центр гиперболы

Рис. 17. Построение касательной

к гиперболе в точке Р:

х – действительная ось;

у – мнимая ось;

О – центр;

А_1, А₂ – вершины;

F_1, F₂ – фокусы

Синусоида – плоская кривая, выражающая закон изменения синуса угла в зависимости от изменения величины угла (рис. 19а).

Величина r называется амплитудой синусоиды, L – длиной волны или периодом синусоиды. (L = 2r).

Для построения синусоиды проводят горизонтальную ось и на ней откладывают заданную длину волны АВ (рис. 19а). Отрезок АВ делят на несколько равных частей, например, на 12. Слева вычерчивают окружность, радиус которой равен величине амплитуды, и делят ее также на 12 равных частей. Точки деления нумеруют и через них проводят горизонтальные прямые. Из точек деления отрезка АВ восстанавливают перпендикуляры к оси синусоиды и на их пересечении с горизонтальными прямыми находят точки синусоиды.

Полученные точки синусоиды а₁, а₂, а₃, … соединяют по лекалу кривой.

При выполнении чертежей деталей или инструментов, поверхности которых очерчены по синусоиде (рис. 19 б, в), величину длины волны АВ обычно выбирают независимо от размера амплитуды r. Например, при вычерчивании шнека (рис. 19 б) длина волны L меньше размера 2r. Такая синусоида называется сжатой. Если длина волны больше размера 2r, то синусоида называется вытянутой.

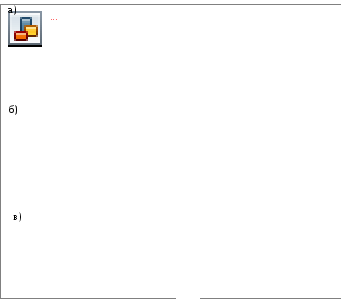
Рис. 19. Построение синусоиды

Для построения касательной к синусоиде в произвольной точке Р (рис. 20) воспользуемся окружностью, по которой строится синусоида, и найдем точку Р₁ на окружности. Проведя касательную в точке Р₁ и найдя на ней точку С эвольвенты, строим точку С^'. Прямая С^'Р является касательной к синусоиде.

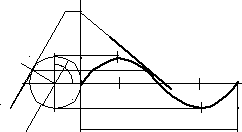
P₁C=AP₁

CC^'//AB

Рис.20. Построение касательной к синусоиде

С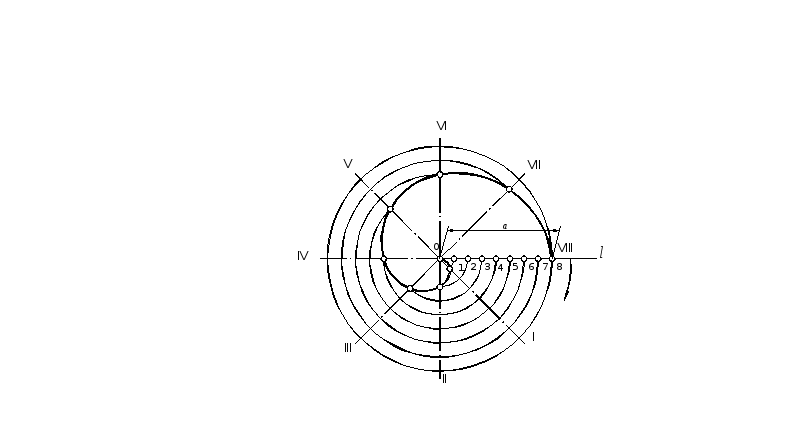 пираль Архимеда (рис. 21) очерчивается точкой О при поступательном равномерном перемещении ее по прямой l при одновременном равномерном вращении последней. Величина поступательного перемещения точки за один оборот прямой l – шаг спирали Архимеда – а.

Рис. 21. Построение спирали Архимеда

Для построения касательной к спирали Архимеда в произвольной точке Р (рис. 22) необходимо построить вспомогательную окружность с центром в точке О и диаметром d = а (d = ОА). Из центра О вспомогательной окружности проводится прямая ОР и перпендикулярно к ней – радиус ОМ. Отрезок МР является нормалью, а перпендикуляр к нему – касательная t к спирали Архимеда в точке Р.

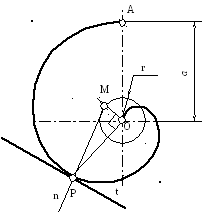a = d r = =

d = 2r

Рис. 22. Построение касательной к спирали Архимеда

Циклоида (греч. кyкloeides - кругообразный ) – траектория точки производящей окружности диаметра d, перекатывающейся без скольжения по прямой линии.

Построение циклоиды по двум точкам сопряжения А и В и известному диаметру производящей окружности d показано на рис. 23. Способ основан на представлении циклоиды как траектории точки А окружности диаметра d, перекатывающейся по прямой х. Возможно, более понятным будет такое построение циклоиды: точка производящей окружности А после перекатывания по оси х окружности на расстоянии А-1 (длина отрезка равна длине дуги А-1) поднимется на высоту h. Начертив окружность d, касающуюся прямую х в точке 1 и воспользовавшись размером h, найдем точку циклоиды.

Рис. 23. Построение циклоиды:

d –диаметр производящей окружности, R – радиус

На рис. 24 показано построение касательной к циклоиде в произвольной точке Р. Воспользовавшись радиусом производящей окружности R=ОС и линией центров этих окружностей, находим центр окружности в положении, когда на ней находится точка Р – точку О₁. Нижнюю точку М вертикального диаметра производящей окружности в рассматриваемом положении соединяем с точкой Р. Прямая МР – нормаль к циклоиде в точке Р. Касательная t перпендикулярна к нормали n.

Рис. 24. Построение касательной к циклоиде

R – радиус производящей окружности

Эвольвента (лат. evolvens – развернутая), другое название инволюта, – плоская кривая, являющаяся разверткой другой кривой эволюты (лат. evoluta - развертываемая). Касательные к эволюте являются нормалями к эвольвенте (рис. 25) или прямыми огибающими ее.

П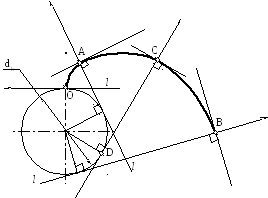остроение эвольвенты окружности по двум точкам сопряжения А и В и основной окружности диаметра d _b показано на рис. 25. Эвольвента описывается в пространстве точкой О прямой l при перекатывании последней по окружности диаметра d _b или точкой О нити, "разматываемой" с окружности диаметра d _b (натяжение нити на рис. 25 показано стрелками).

Рис. 25. Построение эвольвенты окружности диаметра d_b:

d_b - основная окружность (эволюта), О – точка заострения эвольвенты

Произвольная точка эвольвенты С построена на прямой, касающейся основной окружности в точке D из условия что длина отрезка DС равна длине дуги основной окружности ОD.

Для построения касательной к эвольвенте в произвольной точке Р строим касательную Р-8 окружности (рис. 26). Перпендикуляр к Р-8 есть касательная к эвольвенте.

P-8 = A-8

Рис.26. Построение касательной к эвольвенте

 Овал имеет две оси симметрии, овоид – одну, лат.ovum – яйцо

 Асимптота (гр. asymptotos – несовпадающий) – прямая, к которой неограниченно приближается ветвь кривой линии.

 Асимптота (гр. asymptotos – несовпадающий) – прямая, к которой неограниченно приближается ветвь кривой линии.