6. Сопряжения

1. Сопряжение прямых дугами окружностей

Для построения сопряжения двух прямых l и m заданным радиусом R, предварительно находим центр дуги – точку О и точки сопряжения А и В (рис. 7а.б.в).

Точка О найдена, как точка пересечения двух прямых, параллельных, соответственно, прямым l и m и расположенных на расстоянии R. Точки сопряжения А и В – основания перпендикуляров, опущенных из точки О.

Рис. 7. Сопряжение прямых

На рис. 7г радиус дуги сопряжения не задан, но дана прямая с на которой расположен центр дуги – точка О. Для нахождения центра дуги достаточно построить биссектрису угла прямых l и m – прямую k. На пересечении прямых с и k находим точку О. Точки сопряжения А и В и величину радиуса R найдем, опустив перпендикуляры из точки О на прямые l и m.

2. Сопряжение дуги окружности с прямой

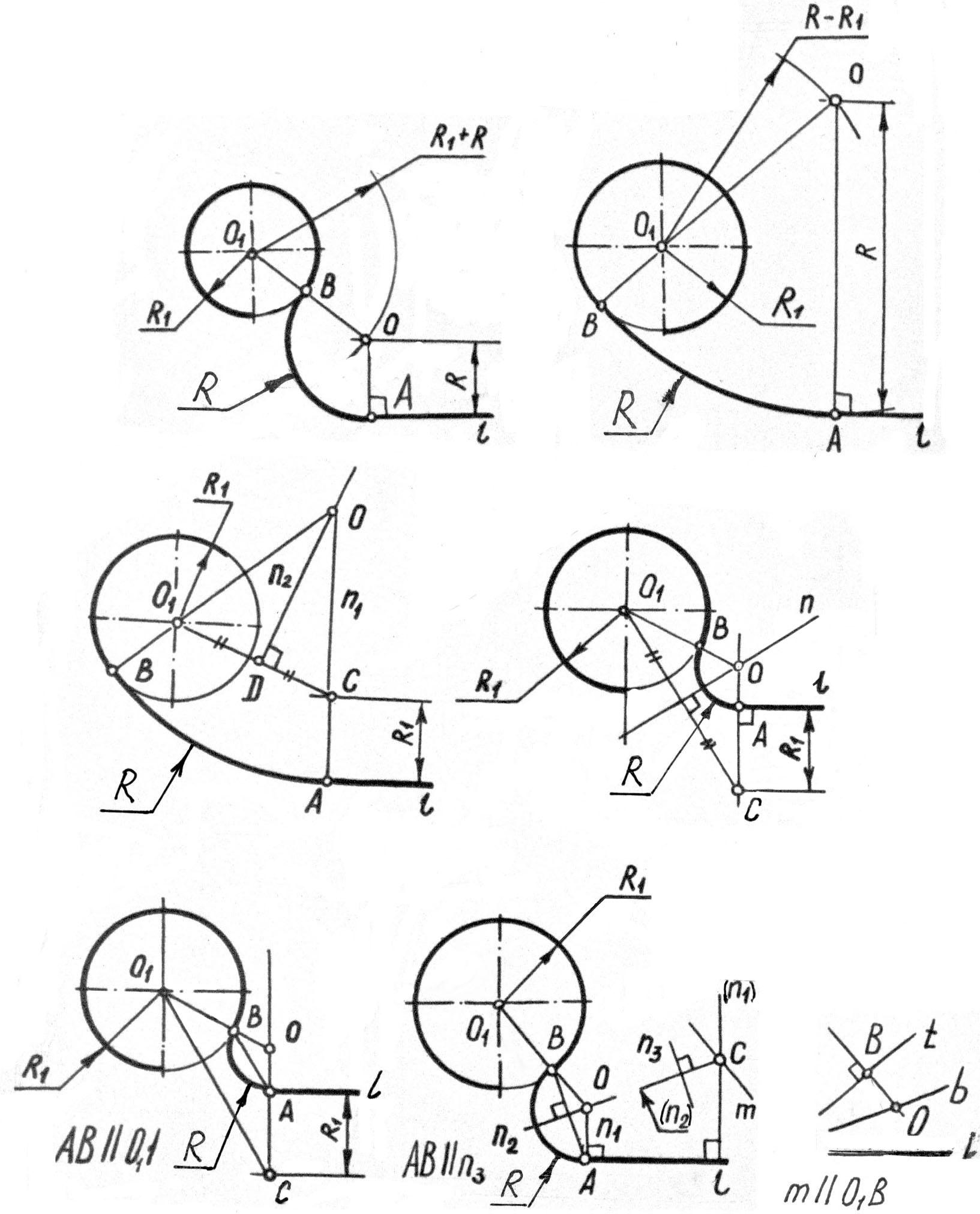
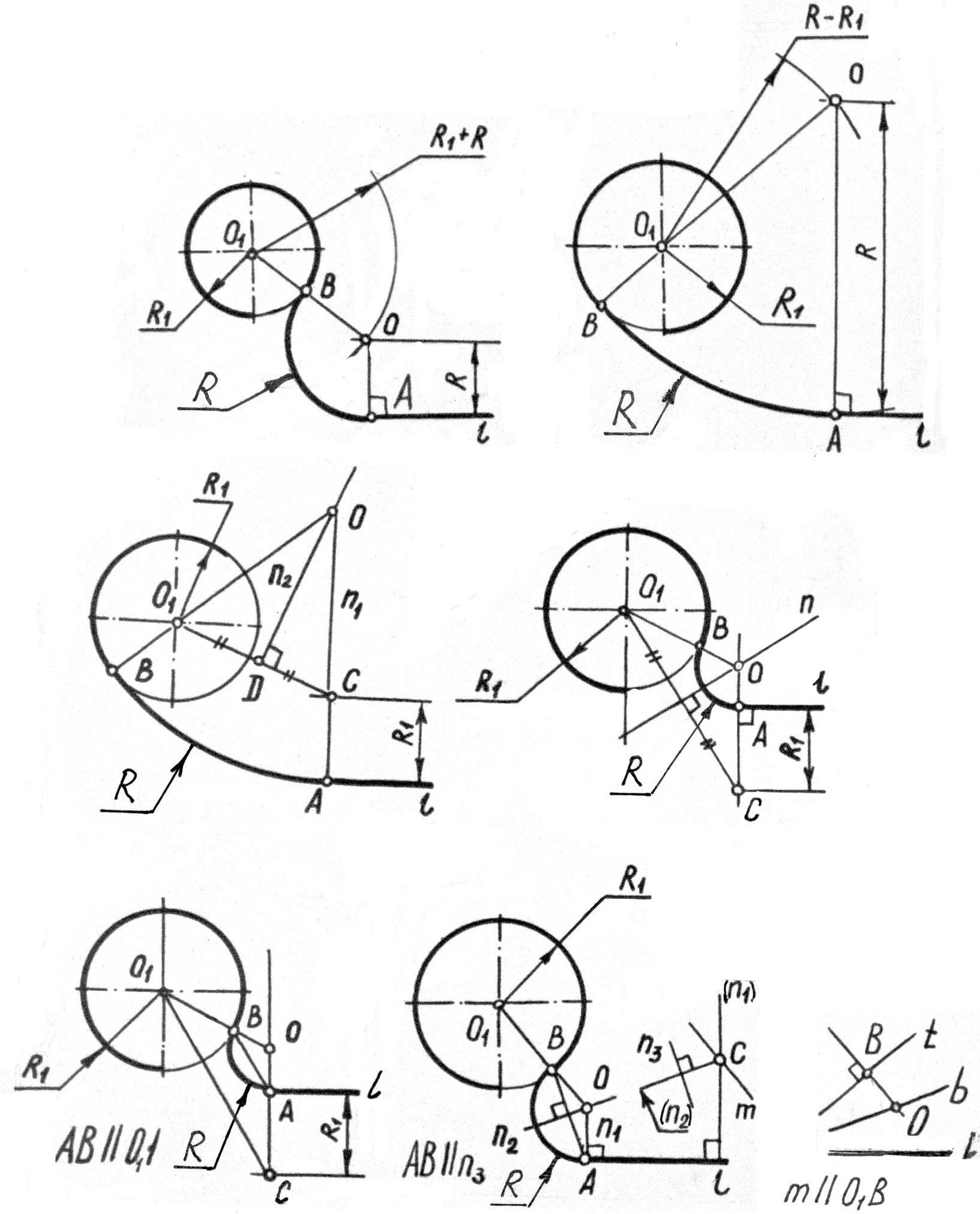
Более сложными являются задачи на сопряжения прямых с дугами окружностей (рис. 8а, б) известен радиус дуги R. Нахождение центра, точки О, радиуса R ясно из рассмотрения рисунков.

В задачах (рис. 8в, г, д) даны дуги радиуса R₁, прямая l и точки сопряжения А на них. Необходимо найти вторую точку сопряжения В и радиус R.

Р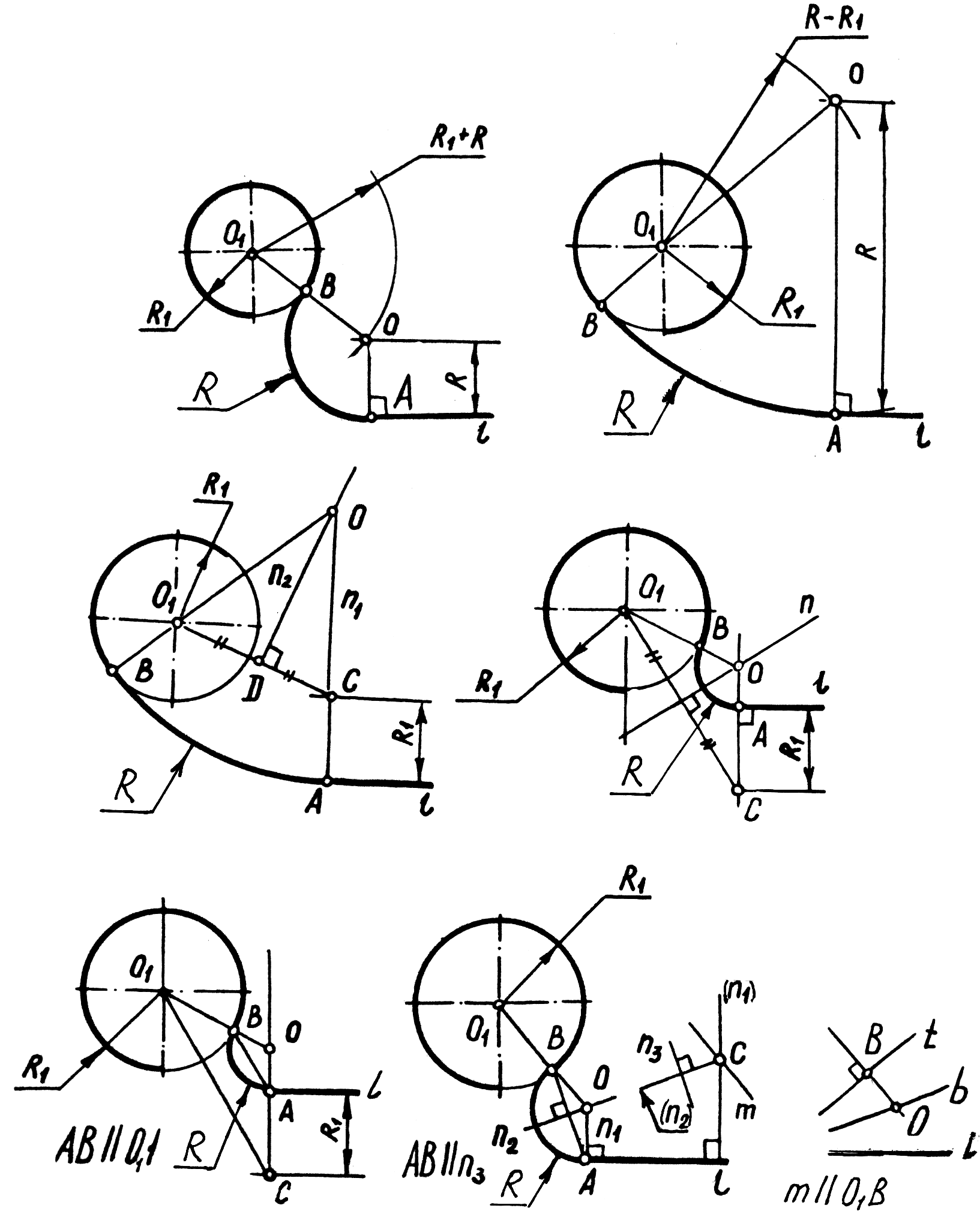ешение задачи (рис. 8в). На перпендикуляре n₁, восстановленном из точки А, находим точку С, соединив точки С и О₁, строим срединный перпендикуляр к отрезку О₁ С .На пересечении перпендикуляров n₁ и n₂ находим точку О, радиус R, а продлив отрезок ОО₁ ,найдем точку В.

а) б)

а) б)

в) г)

д) е)

Ри. 8. Сопряжение окружности с прямой

Задача (рис. 8г) решается аналогично задаче (рис. 8в). Другой вариант решения представлен на рис. 8д. Здесь, построив отрезок О₁С_, точку В находим, проведя прямую АВ  О₁С.

Задача (рис. 8е), решается аналогично задаче (рис. 8в). Для того чтобы найти точку А, достаточно знать направление прямой АВ. На произвольном перпендикуляре (n₁) к прямой l возьмем произвольную точку С, через которую проведем прямую m, m  О₁В. Биссектриса угла между прямыми m и (n₁) – прямая (n₂), а перпендикуляр к прямой (n₂) – прямая n₃ – параллельна прямой АВ.

Из условия АВ  n₃ находим точку А на прямой l . Далее, восстановив срединный перпендикуляр n₂ к отрезку АВ, на пересечении его с перпендикуляром n₁ найдем точку О.

Точку О (рис. 8е) можно найти и другим путем. Достаточно провести касательную t через точку В, и, построив биссектрису b угла между прямыми t и l, на пересечении прямых О₁В и b найдем точку О, радиус R и точку А. Фрагмент решения задачи этим способом показан на рис. 2е справа.

Р

а) б)

в) г)

ассмотренные сопряжения (рис. 9) не всегда возможны. Они невозможны, когда точка А лежит на окружности или когда радиус R, например в случае (рис. 9а), меньше определенной величины. Эту величину можно определить из неравенств: О₁А  О₁О + ОА; О₁  R₁ + R + R; О₁А  R₁ + 2R; R  0,5(О₁А - R₁).

д) е)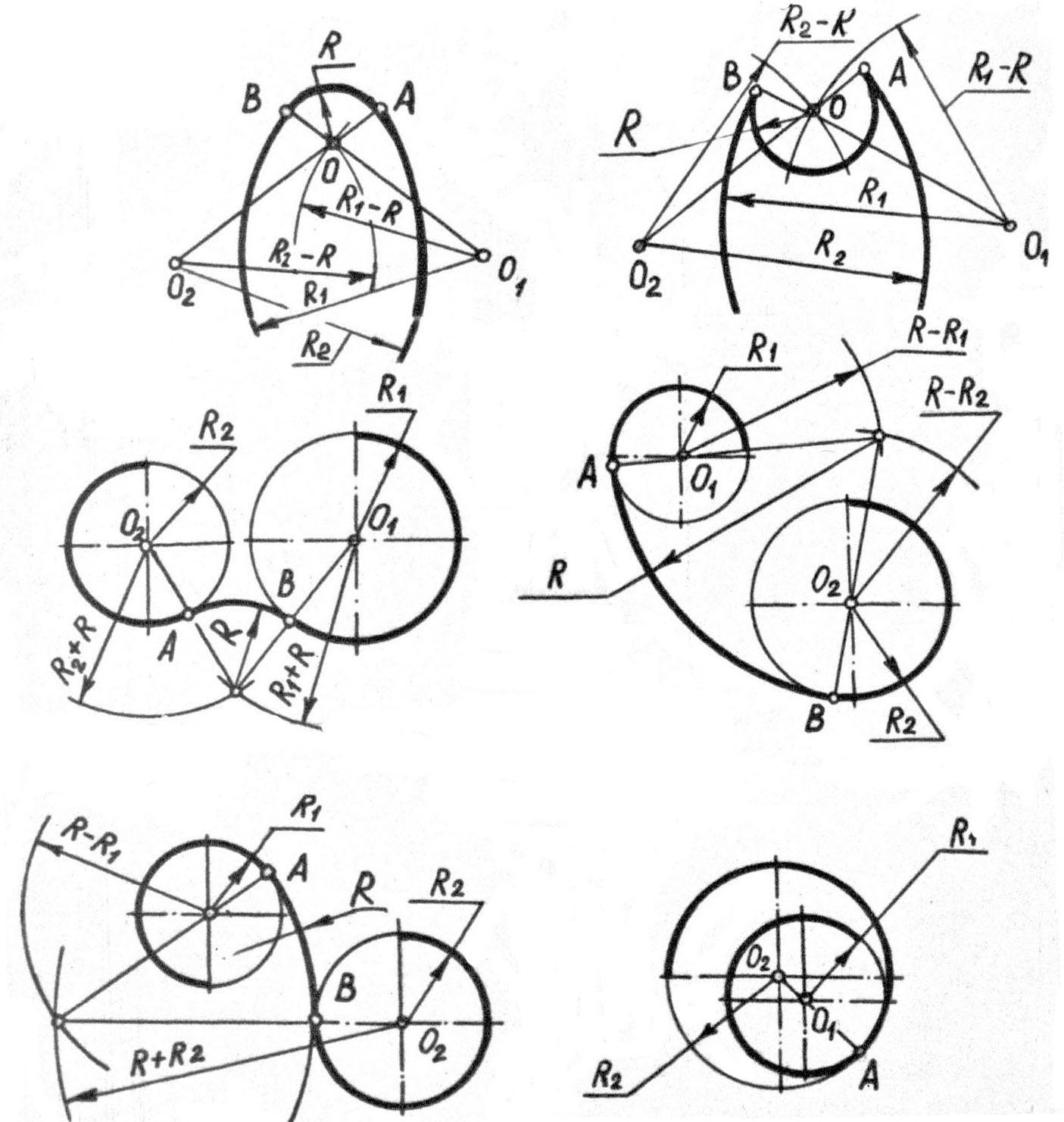

Рис. 9. Сопряжение дуг окружностей

Простейшие случаи сопряжения дуг окружностей представлены на рис. 9. Нахождение центров дуг сопряжения радиуса R, точек О, ясно из рис. 9а, б, в, г, д. Точки перехода А и В расположены на прямых, соединяющих центры дуг радиусов R₁ и R₂, точки О₁ и О₂ с центром дуги сопряжения радиуса R, точкой О.

Дуги радиусов R₁ и R₂ (рис. 9е) имеют одну общую точку А, которая и будет точкой перехода.

Более сложные случаи сопряжения дуг окружностей встречаются в овалах и овоидах^. Овал, полученный сопряжением минимума дуг окружностей, а именно четырех, называется четырехцентровым.