Віднімання двох векторів іможна звести до операції суми

.

Розрізнюють два види перемноження векторів і- скалярне і векторне.

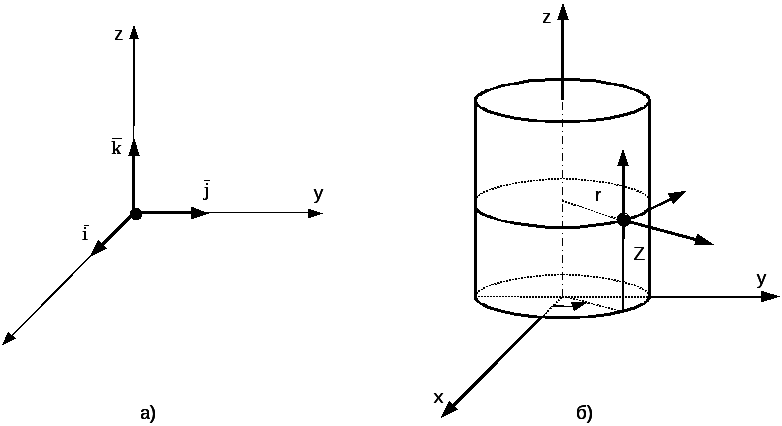
Рисунок В.1

Рисунок В.2

Результатом скалярного добутку є скалярна величина і цю дію подають у вигляді

, (В.2)

де - кут між векторамиі.

Скалярний добуток двох однойменних одиничних векторів

, (В.3)

тому що кут між цими векторами дорівнює нулю.

Скалярний добуток двох різнойменних одиничних векторів

, (В.4)

завдяки тому що кут між векторами дорівнює 90⁰.

Визначимо скалярний добуток між векторами через їхні проекції в прямокутній системі координат

.

Врахувавши (В.3) і (В.4), отримаємо

. (В.5)

Із цього співвідношення видно, що має місце рівність

. (В.6)

Векторним добутком двох векторів іназивають новий вектор , направлений перпендикулярно площині, в якій розміщені векториі,і чисельно рівний

.

Дану операцію записують у вигляді:

. (В.6)

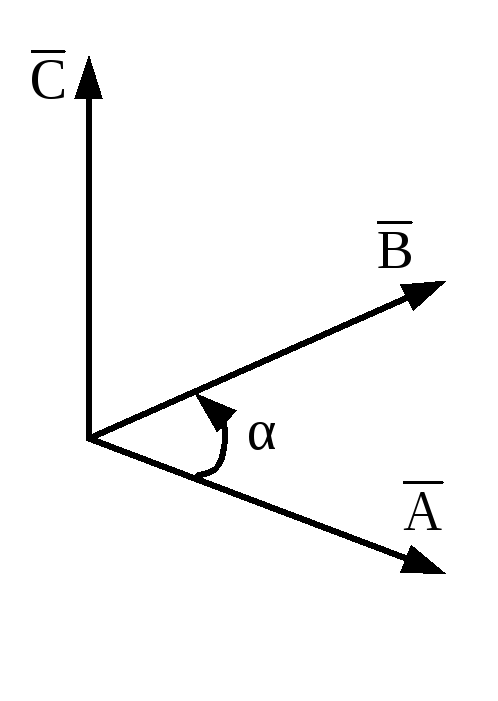
Позитивний напрямок вектора визначають за правилом правоходового гвинта (рис.В.3).

Якщо обертати гвинт в площині векторівівід першого вектора () до другого () по дузі, меншій ніж 180⁰, то поступальний рух гвинта вказує напрямок вектора . З цього правила видно, що

. (В.7)

Векторний добуток можна записати через про-

Рисунок В.3 екції векторів. В прямокутній системі координат

.

Зручно даний вираз записати також у вигляді визначника

. (В.8)

Запишемо ще два добутки:

, (В.9)

. (В.10)

Якщо вектори є неперервними функціями координат, то над ними можна проводити операції диференціювання. У векторному аналізі розрізнюють три види диференціальних операцій.

Векторна просторова похідна () від скалярної функціїB(x,y,z). Якщо похідна взята в напрямку найбільшого зростання функції, то вона називається градієнтом скалярної функції

. (В.11)

В прямокутній системі координат

, (В.12)

в циліндричній

, (В.13)

в сферичній

. (В.14)

Для позначення операції просторового диференціювання часто використовують символ (читається «набла»), який називають диференціальним оператором або оператором Гамільтона, і формально його розглядають як умовний вектор

. (В.15)

Вираз градієнта (В.11) можна розглядати як добуток вектора на скалярну величинуВ

.

Скалярна просторова похідна А від векторної функції називаєтьсядивергенцією векторної функції

. (В.16)

Застосувавши символ , можна записати (В.16) у вигляді скалярного добутку двох векторів

. (В.16)

Для прямокутної системи координат

, (В.17)

для циліндричної

, (В.18)

для сферичної

. (В.19)

Векторна просторова похідна від векторної функціїназиваєтьсяротором функції

. (В.20)

В різних системах координат цю похідну зручно записувати у вигляді визначника.

В прямокутній системі координат

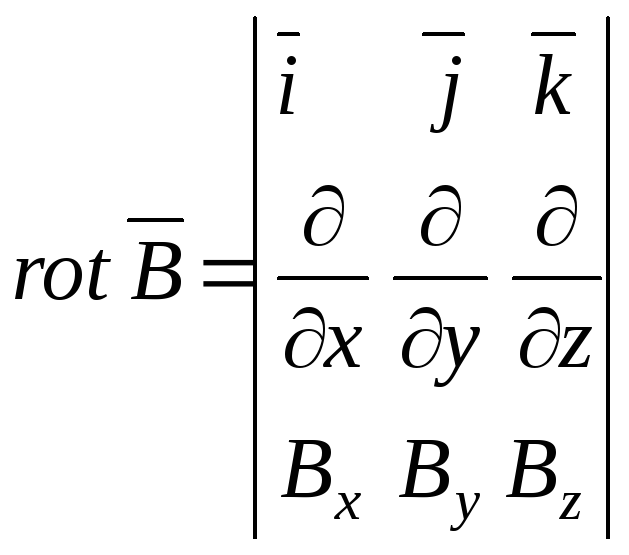, (В.21)

в циліндричній

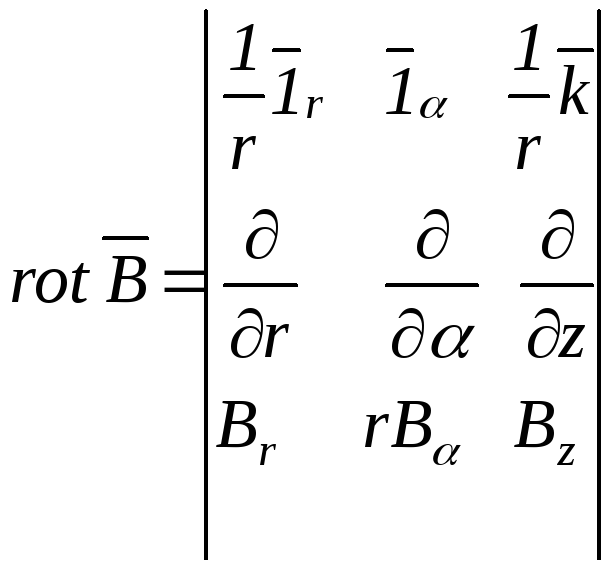, (В.22)

в сферичній

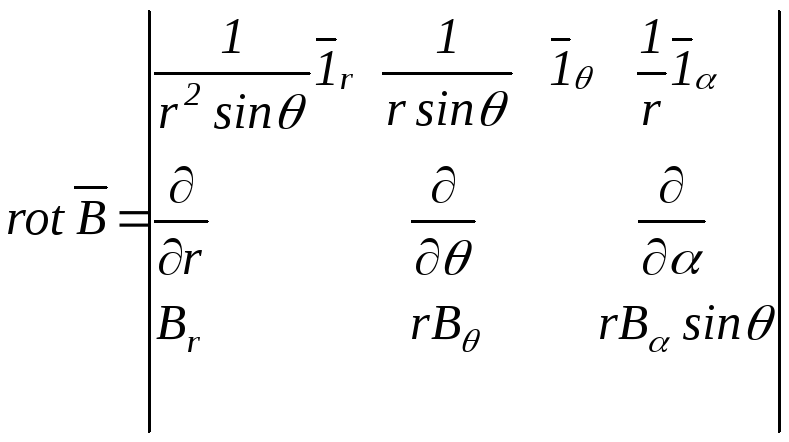. (В.23)

Вираз (В.20) можна записати як векторний добуток векторів і

. (В.24)

Згадаємо ще декілька співвідношень

, (В.25)

. (В.26)

Теорема Остроградського-Гаусса

. (В.27)

Інтеграл від вектора по замкненій поверхні дорівнює інтегралу від дивергенції даного вектора по об’єму , що обмежений поверхнею.

Теорема Стокса

. (В.28)

Інтеграл від вектора вздовж замкненого контуру l дорівнює інтегралу від ротора вектора по поверхні, що обмежена контуромl.