3.8 Приклади розрахунку електричних полів

в провідному середовищі

Приклад 3.1

В провідному середовищі з провідністю потенціал поля змінюється за таким законом

,

де і– координати прямокутної системи координат (рис.3.8),

–числові коефіцієнти.

Знайти закономірність зміни густини струму в залежності від координат і визначити силу струму, що протікає через квадратну площину зі стороною , яка розташована паралельно площиніі знаходиться на відстанівід неї.

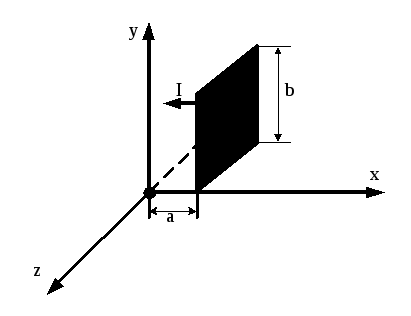
Рисунок 3.8

Розв’язування. В областях без сторонньої напруженості . В прямокутній системі координат напруженість поля визначається

і має складові по осі та по осі.

Вектор густини струму

також має складові тільки по осі і по осі.

В зв’язку з тим, що площинка через яку необхідно розрахувати величину струму, що протікає, паралельна площині , то через неї проходить тільки складова вектора густини. Ця складова не залежить ні від координати, ні від координати. Тому вона постійна для усіх точок площинки і її величина визначається при

.

Значення струму визначається як добуток складової на розмір площадки

.

Знак мінус показує на те, що струм протікає справа наліво.

Приклад 3.2

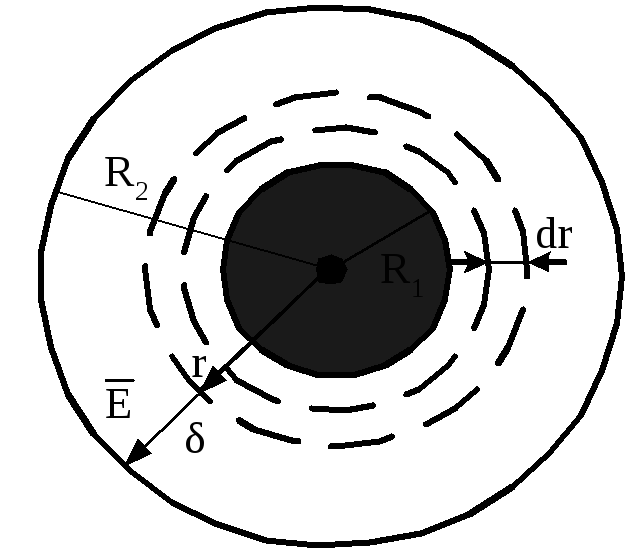В коаксіальному кабелі (рис.3.9) діелектрик між внутрішнім проводом і оболонкою має провідність. Радіус внутрішнього провідника, радіус оболонки. Напруга між провідниками кабеля. Визначити провідність ізоляції кабелю на одиницю його довжини, струм витікання і потужність теплових втрат.

Розв’язування. Приймемо потенціал зовнішньої оболонки рівним нулю, тоді вектор напруженості електричного поля і вектор густини струмунаправлені по радіусу від внутрішнього провідника до оболонки. Обведемо внутрішній провідник кабелю циліндричною поверхнеюрадіусаі довжиною.

Рисунок 3.9 Струм, що протікає через цю поверхню визначається

.

В зв’язку з тим, що вектори ізбігаються за напрямком і в силу симетрії величина густини струму на поверхнівсюди однакова, то можна записати

.

Звідки

.

Напруга між провідниками кабелю визначається

.

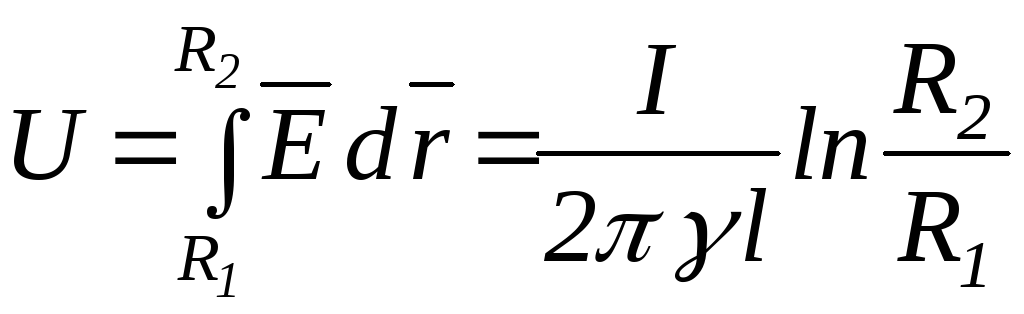Провідність ізоляції всього кабелю становить

.

Провідність ізоляції одиниці довжини кабелю

.

Струм витікання на одиницю довжини кабелю

.

Потужність теплових втрат в ізоляції всього кабелю (3.19)

.

За елемент об’єму вибираємо величину .

В цьому випадку

.

Потужність теплових втрат ізоляції в одиниці довжини кабелю

.

Цю потужність можна знайти для даного випадку і простіше. На постійному струмі

.

Приклад 3.3

Півсферичний заземлювач радіусом розміщено в землі на рівні з її поверхнею (рис.3.10). Відомий струм, що протікає через заземлювач. Визначити опір заземлення і напругу між точкамиіна поверхні землі (крокову напругу). Провідність землі,,.

Рисунок 3.10

Розв’язування. Припустимо, що струм повертається до джерела по землі по другому електроду, який знаходиться достатньо далеко від першого.

Для цього припущення можна вважати, що струм розтікається від заземлювача у всі сторони рівномірно, тому густина струму для всіх точок півсфери радіуса однакова і дорівнює

.

Напруженість поля в точках цієї півсфери знаходимо за законом Ома в диференціальній формі

.

Вектори інаправлені по радіусу (рис.3.10).

Якщо прийняти потенціал точки, що знаходиться в нескінченості , рівним нулю, то потенціал на поверхні заземлювача визначається

.

Напруга

називається напругою розтікання.

Опір заземлення становить

.

Крокова напруга визначається

.

Підставивши числові значення отримаємо

.

.

Приклад 3.4

Провідник, по якому протікає постійний струм , обірвався і упав на землю на дуже велику довжину(рис.3.11).

Визначити крокову напругу, під якою буде знаходитися людина з довжиною кроку , і яка наближається перпендикулярно до провідника. Відстань від провідника до ближньої ноги людини. Провідність землі.

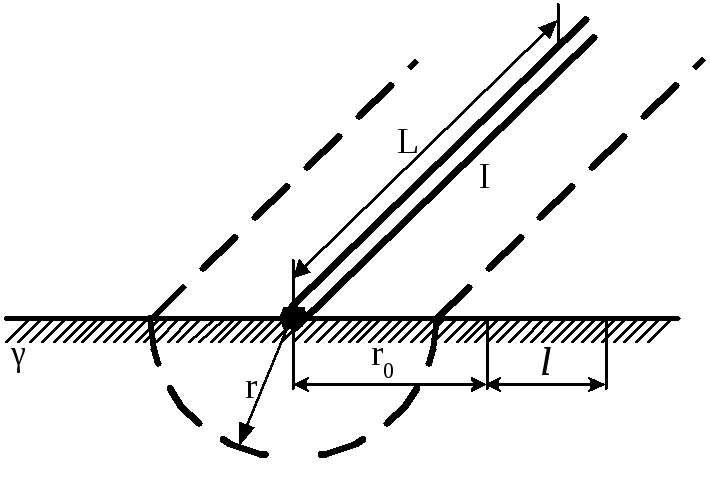
Рисунок 3.11

Розв’язування. Дана задача розв’язується аналогічно попередній. Густина струму в точках півциліндричної поверхні радіуса від осі провідника

.

Напруженість поля в точках цієї поверхні

.

Крокова напруга визначається

.

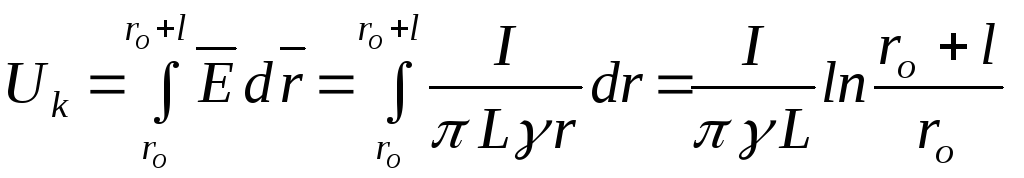Підставивши числові значення, отримаємо

.