
- •Т е о р е т и ч н і
- •Вінниця внту 2004
- •II методи розрахунку електростатичного
- •III електричне поле постійних струмів
- •В с т у п
- •Віднімання двох векторів іможна звести до операції суми
- •Iелектростатичне поле
- •1.1 Закон Кулона
- •Скалярний добуток
- •Врахувавши попереднє, отримуємо
- •Різниця потенціалів між точками івизначається
- •Звідси визначаються проекції напруженості поля по осях координат
- •1.13 Теорема єдиності розв’язку
- •Контрольні питання
- •II методи розрахунку електростатичного поля
- •2.2 Застосування співвідношень, які пов’язані з законом Кулона
- •2.3 Застосування теореми Гаусса Приклад 2.5
- •Приклад 2.6
- •Приклад 2.7
- •Приклад 2.8
- •Приклад 2.9
- •Приклад 2.10
- •Приклад 2.11
- •Приклад 2.12
- •Приклад 2.13
- •Приклад 2.14
- •2.5 Розподіл потенціалів і зарядів в системі заряджених тіл
- •Приклад 2.17
- •2.6 Застосування рівнянь Пуассона і Лапласа
- •III електричне поле постійних струмів в провідному середовищі
- •3.3 Напруженість сторонніх сил. Електрорушійна сила
- •3.4 Закони Кірхгофа в диференціальній формі
- •3.5 Диференціальна форма закону Джоуля-Лєнца
- •3.6 Електричне поле в провідному середовищі
- •3.7 Аналогія між електричним полем в провідному середовищі
- •Таблиця
- •3.8 Приклади розрахунку електричних полів
- •Контрольні питання
- •Література
- •Навчальне видання
3.4 Закони Кірхгофа в диференціальній формі
Визначимо
потік вектора густини струму
![]() (електричний
струм
(електричний
струм
![]() )
через замкнену поверхню
)
через замкнену поверхню![]() ,
яка включає в себе декілька відгалужень
зі струмами, які сходяться в одному
вузлі (рис.3.5).
,
яка включає в себе декілька відгалужень
зі струмами, які сходяться в одному
вузлі (рис.3.5).
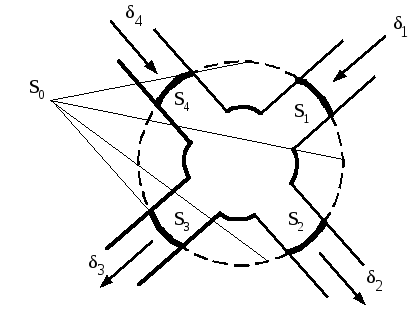
Рисунок 3.5
Як
показано раніше, в будь-якому місці кола
не можуть постійно накопичуватися
заряди при протіканні струму, тому сума
вхідних струмів (![]() )
в об’ємі, що обмежений поверхнею
)
в об’ємі, що обмежений поверхнею![]() ,
повинна дорівнювати сумі вихідних
струмів із даного об’єму (
,
повинна дорівнювати сумі вихідних
струмів із даного об’єму (![]() ).
).
Розіб’ємо
всю замкнену поверхню на поверхню
![]() ,
що не включає в себе поперечний переріз
провідників, і на поверхні, які
представляють собою поперечний переріз
провідників
,
що не включає в себе поперечний переріз
провідників, і на поверхні, які
представляють собою поперечний переріз
провідників![]()
![]() ,
,
тоді
![]() ,
,
де
![]() – густина струму у відповідних перерізах.
– густина струму у відповідних перерізах.
В
зв’язку з тим, що
![]() (
(![]() – поверхня, що не включає провідники),
а
– поверхня, що не включає провідники),
а
![]() ,
,
то
![]() .
.
Знак
мінус біля струмів
![]() і
і![]() поставлено тому, що усі вектори
поставлено тому, що усі вектори![]() направлені із об’єму (позитивний
напрямок), а вектори густини струмів
направлені із об’єму (позитивний
напрямок), а вектори густини струмів![]() і
і![]() направлені в об’єм, що розглядається.
направлені в об’єм, що розглядається.
В зв’язку з тим, що сума вхідних і вихідних струмів повинна бути рівною між собою (перший закон Кірхгофа), то
![]() .
(3.13)
.
(3.13)
Отже, інтеграл від густини струму по замкненій поверхні завжди дорівнює нулю. Рівняння (3.13) виражає перший закон Кірхгофа в інтегральній формі.
Якщо до (3.13) застосувати теорему Остроградського-Гаусса (В-27), то
![]() .
(3.14)
.
(3.14)
Останнє співвідношення називають першим законом Кірхгофа в диференціальній формі. Воно показує, що лінії густини постійного струму завжди замкнені, в них немає початку і вони ніколи не закінчуються. Дивергенція густини струму завжди дорівнює нулю, що виражає принцип неперервності електричного струму.
Запишемо диференціальну форму закону Ома (3.5) при наявності сторонньої напруги
![]()
або
![]() .
(3.15)
.
(3.15)
Візьмемо лінійний інтеграл від обох частин рівняння (3.15) по замкненому контуру електричного кола
![]() .
(3.16)
.
(3.16)
Перетворимо
інтеграл в лівій частині останнього
рівняння так. Помножимо і розділимо
підінтегральний вираз на площу поперечного
перерізу провідника
![]() .
При постійному струмі густина струму
по всьому перерізу постійна і збігається
за напрямком з елементом довжини
.
При постійному струмі густина струму
по всьому перерізу постійна і збігається
за напрямком з елементом довжини![]() ,
тому
,
тому
![]()
і
![]() .
.
Якщо в контурі є відгалуження з різними за значенням струмами і опорами, то
![]() ,
,
де
![]() – опір окремих ділянок контуру.
– опір окремих ділянок контуру.
В правій частині рівняння (3.16) другий інтеграл дорівнює нулю (замкнений інтеграл береться від напруженості електростатичного поля), а перший інтеграл представляє собою суму е.р.с. (3.8), що входять в досліджуваний контур. Отже,
![]() ,
(3.17)
,
(3.17)
що відповідає рівнянню, яке отримують для другого закону Кірхгофа. Тому рівняння (3.15) називають другим законом Кірхгофа в диференціальній формі.
3.5 Диференціальна форма закону Джоуля-Лєнца
Нехай
елементарний заряд
![]() ,
який зосереджено в паралелепіпеді
(рис.3.2) рухається під дією сил електричного
поля. Сила, яка переміщує заряд, дорівнює
,
який зосереджено в паралелепіпеді
(рис.3.2) рухається під дією сил електричного
поля. Сила, яка переміщує заряд, дорівнює![]() .
Робота, що витрачається для переміщення
заряду на відстань
.
Робота, що витрачається для переміщення
заряду на відстань![]()
![]() .
.
Якщо
заряд проходить відстань
![]() за проміжок часу
за проміжок часу![]() ,
то потужність
,
то потужність
![]() .
.
Відношення
![]() є струм
є струм![]() ,
що протікає по досліджуваному об’ємі,
тому
,
що протікає по досліджуваному об’ємі,
тому
![]() .
.
В
зв’язку з тим, що
![]() є елементом об’єму, то
є елементом об’єму, то
![]() .
.
Звідси потужність, віднесена до одиниці об’єму (питома потужність)
![]() .
(3.18)
.
(3.18)
Рівняння (3.18) називають законом Джоуля-Лєнца в диференціальній формі.
Потужність,
яка поглинається в деякому провіднику
з об’ємом
![]()
![]() .
(3.19)
.
(3.19)
Визначимо
потужність через інтегральні характеристики
(струм, напругу). Для паралелепіпеда
(рис.3.2) напруга між його кінцями
![]() ,
а струм що в ньому протікає
,
а струм що в ньому протікає![]() .
Замінимо в (3.19)
.
Замінимо в (3.19)![]() і
і![]() на струм і напругу
на струм і напругу
![]()
або
![]() .
.
Останній вираз можна назвати законом Джоуля-Лєнца в інтегральній формі.
