
- •Тема: Исследование устойчивости нелинейных систем
- •Тема: Исходные положения метода гармонической линеаризации (мгл)
- •Тема: Метод точечного преобразования
- •Тема: Метод фазового пространства (исходные положения)
- •Тема: Особенности нелинейных динамических систем
- •Тема: Описание случайных процессов
- •Тема: Фазовые параметры динамических систем.
- •Частотный критерий абсолютной устойчивости.
- •Тема: Частотный способ определения симметричных автоколебаний.
- •Виды нелинейностей.
Тема: Метод точечного преобразования
44. На рисунках (17. gif), (18.gif) даны вид отрезка без контакта АВ с заданной системой координат и график функции последования совместно с биссектрисой координатного угла. Определить тип колебательных движений динамической системы.

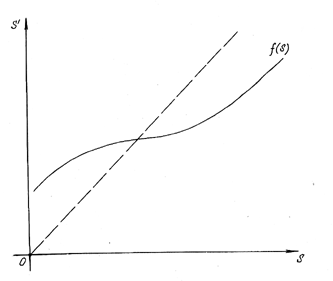
а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - неустойчивый, внешний цикл – устойчивый;
г) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - устойчивый, внешний цикл – неустойчивый;
45. На рисунках (17. gif), (19.gif) даны вид отрезка без контакта АВ с заданной системой координат и график функции последования совместно с биссектрисой координатного угла. Определить тип колебательных движений динамической системы.
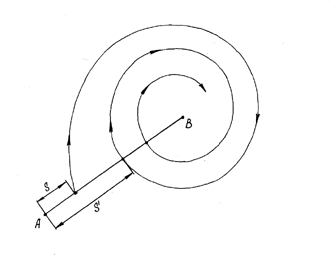

а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - неустойчивый, внешний цикл – устойчивый;
г) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - устойчивый, внешний цикл – неустойчивый;
46. На рисунках (17. gif), (20.gif) даны вид отрезка без контакта АВ с заданной системой координат и график функции последования совместно с биссектрисой координатного угла. Определить тип колебательных движений динамической системы.


а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - неустойчивый, внешний цикл – устойчивый;
г) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - устойчивый, внешний цикл – неустойчивый;
47. На рисунках (17. gif), (21.gif) даны вид отрезка без контакта АВ с заданной системой координат и график функции последования совместно с биссектрисой координатного угла. Определить тип колебательных движений динамической системы.

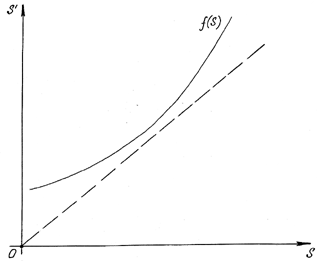
а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) расходящиеся колебания;
г) затухающие колебания;
48. На рисунках (17. gif), (22.gif) даны вид отрезка без контакта АВ с заданной системой координат и график функции последования совместно с биссектрисой координатного угла. Определить тип колебательных движений динамической системы.


а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) расходящиеся колебания;
г) затухающие колебания;
49. На рисунках (17.gif), (23.gif) даны вид отрезка без контакта АВ с заданной системой координат и график точечного преобразования в параметрической форме (t- время). Определить тип колебательных движений динамической системы.


а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - неустойчивый, внешний цикл – устойчивый;
г) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - устойчивый, внешний цикл – неустойчивый;
50. На рисунках (17.gif), (24.gif) даны вид отрезка без контакта АВ с заданной системой координат и график точечного преобразования в параметрической форме (t- время). Определить тип колебательных движений динамической системы.


а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - неустойчивый, внешний цикл – устойчивый;
г) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - устойчивый, внешний цикл – неустойчивый;
51. На рисунках (17.gif), (25.gif) даны вид отрезка без контакта АВ с заданной системой координат и график точечного преобразования в параметрической форме (t- время). Определить тип колебательных движений динамической системы.
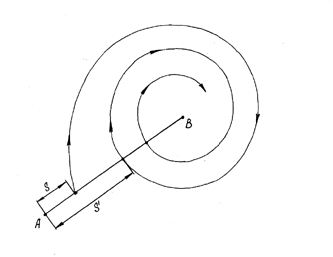

а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - неустойчивый, внешний цикл – устойчивый;
г) два, вложенных друг в друга, предельных цикла, из которых внутренний цикл - устойчивый, внешний цикл – неустойчивый;
52. На рисунках (17. gif), (26.gif) даны вид отрезка без контакта АВ с заданной системой координат и график функции последования совместно с биссектрисой координатного угла. Определить тип колебательных движений динамической системы.


а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) расходящиеся колебания;
г) затухающие колебания;
53. На рисунках (17. gif), (27.gif) даны вид отрезка без контакта АВ с заданной системой координат и график функции последования совместно с биссектрисой координатного угла. Определить тип колебательных движений динамической системы.


а) устойчивый предельный цикл автоколебания;
б) неустойчивый предельный цикл;
в) расходящиеся колебания;
г) затухающие колебания;
54. Какой фазовой траектории соответствует случай совпадения последующей точки точечного преобразования отрезка без контакта с исходной точкой?
незамкнутой траектории
замкнутой траектории
асимптоте седлового состояния равновесия
отрезку покоя
55. Какой метод является основой метода точечного преобразовния?
метод разделения движений
метод припасовывания
метод гармонического баланса
прямой метод Ляпунова
56. На основе теоремы Кенигса определите условие устойчивости предельного цикла.
1.
 2.
2.
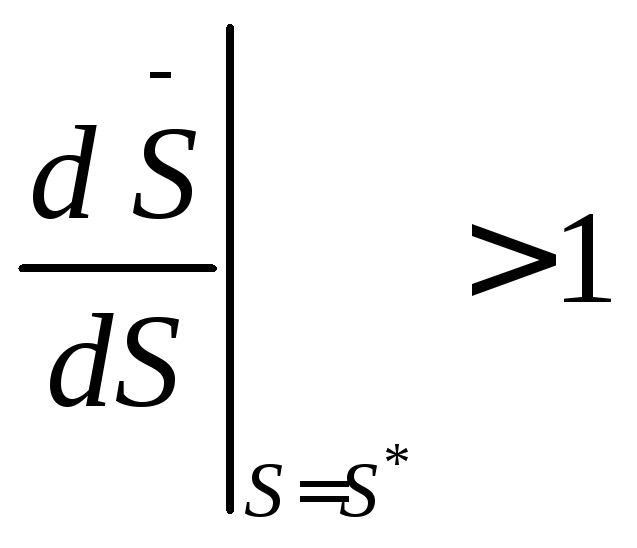 3.
3.
 4.
4.
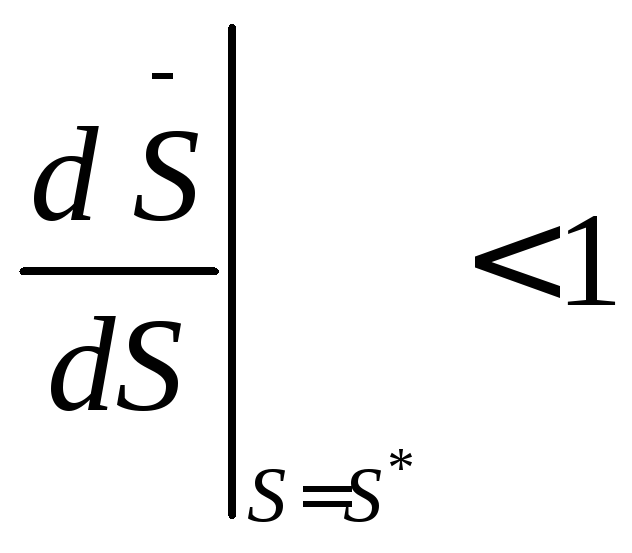
57. Какой тип устойчивости периодического движения определяется теоремой Кенигса об устойчивости предельного цикла?
устойчивость «в большом»
устойчивость «в малом»
абсолютная устойчивость
устойчивость «в целом»
58. К какому классу методов относится метод точечного преобразования?
точный аналитический метод, ориентированный на динамические системы высокого порядка
точный аналитический метод, ориентированный на системы невысокого порядка
приближенный аналитический метод, ориентированный на системы высокого порядка
приближенный аналитический метод, ориентированный на системы невысокого порядка
59. Что такое отрезок без контакта в методе точечного преобразования?
отрезок прямой или дуги гладкой кривой, в точках которого фазовые траектории системы касаются его
отрезок прямой, являющейся асимптотой для фазовых траекторий системы
отрезок покоя
отрезок прямой или дуги гладкой кривой, в каждой точке которого фазовые траектории пересекают его, нигде не касаясь.
60. Что является условием существования функции последования точечного преобразования?
свойство возвращаемости изображающей точки на отрезок без контакта за любое время
возвращаемость изображающей точки на отрезок без контакта за конечный промежуток времени
асимптотическое приближение изображающей точки к отрезку покоя
наличие на отрезке без контакта особой точки динамической системы
61. Какое свойство функции последования точечного отображения вытекает из теоремы Коши о существовании единственности решения?
1.
 2.
2.
 3.
3.
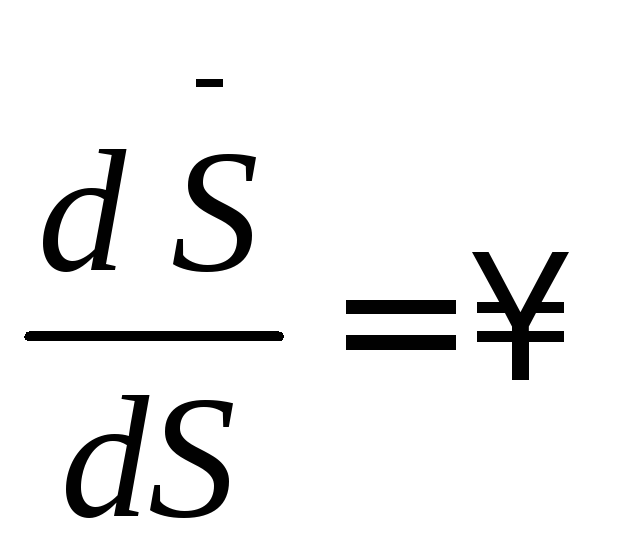 4.
4.

62. Какой вид устойчивости предельного цикла можно определить с помощью «лестницы Ламерея» в методе точечного отображения
устойчивость «в малом»
устойчивость «в большом»
абсолютную устойчивость
