2. Логический вывод в байесовских сетях доверия с непрерывными и дискретными состояниями

Логический вывод в таких БСД заключается в распространении вероятностей и параметров гауссовских законов распределения по всей сети в зависимости от полученных свидетельств. В частности, для рассматриваемого примера для исходного набора данных будут получены оценки производственных затрат:

m_п.з= 7483,33

s _п.з= 1208,1

Однако эти оценки могут быть пересчитаны для случая иной загрузки оборудования или получения новых свидетельств о ставках аренды или нормах амортизации. Наряду с этим возможен и обратный вывод в этой простейшей экспертной системе. Он, например, может заключаться в определении допустимых ставок арендных плат при возможном значении суммарных производственных затрат.

В основе процесса логического вывода лежат довольно сложные математические алгоритмы, которые мы рассмотрим на простейшей двухуровневой сети для случая прямого распространения распределения вероятностей.

Пусть независимые дискретные случайные величины X₁,...,X_sи непрерывные случайные величиныZ₁,...,Z_rоказывают влияние на результирующую случайную величинуY.

Рис.2.8.4. Двухуровневая БСД с непрерывными и дискретными переменными.

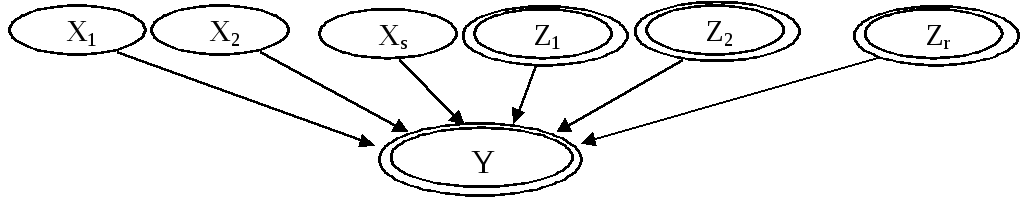
Каждая из дискретных случайных величин имеет своими исходами значения с вероятностямиP_ij, для которых . Совместное влияние дискретных случайных величин наYхарактеризуется математическим ожиданием и дисперсиями . Каждая из непрерывных случайных величин имеет непрерывное нормальное распределение с параметрами , где . Совместное влияние непрерывной случайной величиныи исходов дискретных величин на результирующую случайную величинуYхарактеризуется весовыми коэффициентами для .

Тогда характеристики результирующей величины Yмогут быть вычислены по следующим выражениям:

В частности, для рассмотренного выше примера, содержащего две исходные непрерывные (r= 2) переменные и одну дискретную (s= 1) переменную, имеющую три исхода (n₁=3), числовые характеристики случайной переменной «Производственные затраты» будут

0,333 ×(3000 + 50000×0,075 + 0,6×2500) +

0,333 ×(3200 + 40000×0,075 + 0,5×2500) +

0,333 ×(3500 + 3000×0,075 + 0,4×2500) =

0,333 ×(8250 + 7450 + 6750)= =7483,33

Полученные в результате математического расчета выводы полностью совпадают с результатами, выдаваемые системой Huginдля аналогичной модели БСД.

Лекция 9

2.9 Экспертные системы на основе теории Демстера–Шеффера (тдш).

2.9.1 Предпосылки возникновения новой теории.

При использовании теории вероятностей для представления неопределенных знаний исследователи столкнулись с рядом трудностей. Это стимулировало возникновение новой теории, которая была разработана в 1960 г Демстером и в дальнейшем развита Шеффером (1970 год). Она получила название "теории Демстера-Шеффера" (ТДШ).

Основными предпосылками ее возникновения явилось преодоление ряда ограничений, накладываемых классической теорией вероятностей на предоставление неопределенных знаний. К разряду таких ограничений обычно относят следующие:

• представление полного незнания, когда мы ничего не знаем об объекте;

• жесткие условия 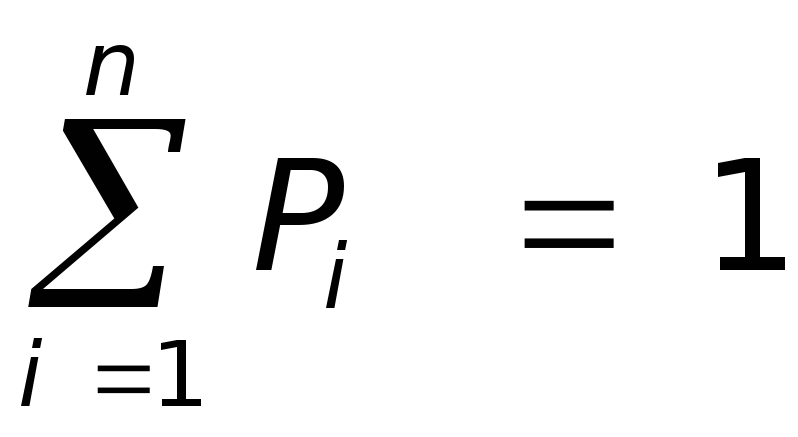, что требует знания или определения вероятностей всех возможных исходов (гипотез);

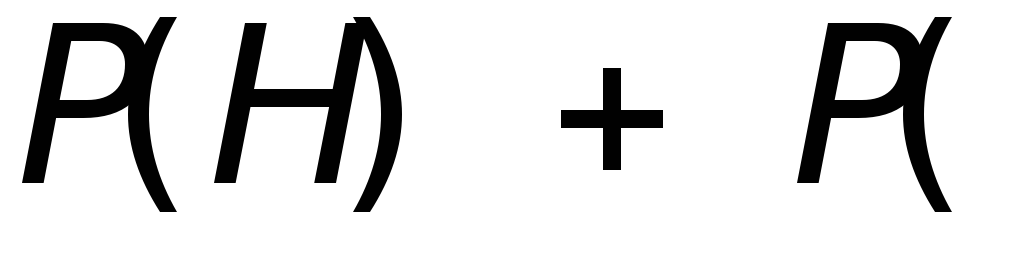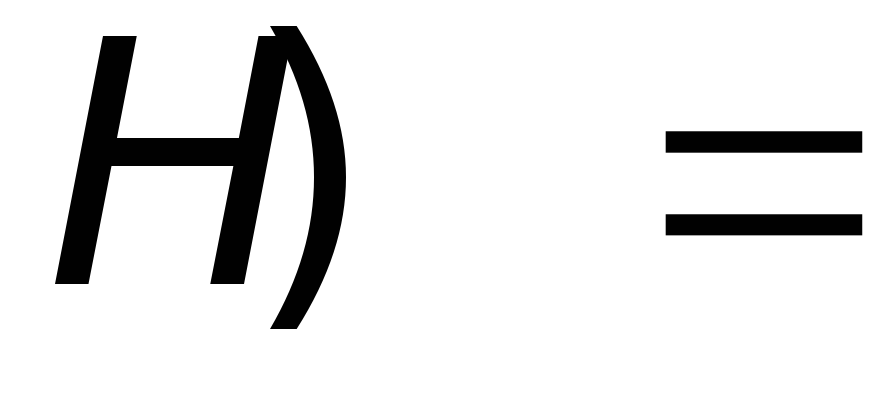• фиксирования вероятности отрицательной гипотезы вероятностью прямой гипотезы, т.к. ù1.

Первое ограничение связано с тем, что традиционный байесовский подход представляет незнание (неосведомленность) равномерными вероятностями. Некоторый недостаток этого подхода заключается в том, что равномерное распределение вероятности, оказывается, представляет большую информацию, чем дано.

Так, например, если эксперт утверждает, что из всех возможных видов транспортировки груза, мы должны воспользоваться речным транспортом ("РТ"), либо железнодорожным ("ЖД"), то это говорит о степени незнания эксперта и совсем не означает, что вероятности возможной транспортировки будут Р("РТ")=0,5 и Р("ЖД")=0,5.

Второе ограничение определяется тем, что психологически во многих ситуациях эксперту сложно оставаться в рамках строгого математического аппарата теории вероятностей, которая по своей природе носит объективный характер. Необходимо нарушить жесткие условия равенства единице сумм вероятностей всех исходов, особенно при большом их количестве.

В большинстве случаев реально наблюдаемые свидетельства подтверждают не какой-либо конкретный исход (или гипотезу) а сразу же некоторое множество, что не позволяет определить вероятность каждого из них. Так, если мы на 90% уверены в том, что промчавшийся мимо нас автомобиль - это "Жигули", то эта масса уверенности (m₁=0.9) относится ко всем моделям "Жигулей", а масса уверенности m₂=0.1 – ко всем прочим маркам легковых автомобилей, причем более детальное её распределение нам неизвестно.

Что касается третьего ограничения, то, как следует из множества реальных ситуаций, свидетельства, которые только частично поддерживают гипотезу не следует рассматривать как свидельство также поддерживающее отрицание гипотезы.