Глава 2

моды оптических волноводов

2.1. Предварительный анализ волноводных процессов распростра-нения оптического излучения в оптических волноводах. Из курса физической оптики [1] известно, что распространение световых волн в материальных средах описывается уравнениями Максвелла, которые для непроводящего и свободного от зарядов материала волновода можно записать в виде

(2.1.1)

где ,- векторы напряженности электрического и магнитного поля соответственно;₀,₀- диэлектрическая и магнитная проницаемости вакуума соответственно;n(x,y,z)- распределение показателя преломления в материале световода.

В общем случае вектора иимеют по три декартовые компоненты. Это означает, что при записи в скалярном виде - для всех декартовых проекций векторов, общее число уравнений в системе (2.1.1) становится равным двенадцати. Решить такую систему достаточно сложно. Подробное и строгое решение указанной системы для оптических волноводов выходит за рамки данного пособия и заинтересованным читателям советуем обратиться к более фундаментальным учебникам [2-4, 9-11]. В настоящем пособии получение основных представлений о волновом подходе будет базироваться на ряде приближений, позволяющих значительно упростить математические вычисления. При этом сначала будет проведен качественный анализ волноводных процессов распространения оптического излучения. Далее эти процессы будут более детально изучены применительно к простым, но практически важным случаям симметричного планарного волновода и волоконного световода круглого сечения.

Основным методом решения уравнений Максвелла является метод мод. В этом методе электромагнитное поле направляемого излучения представляется в виде разложения в ряд по дискретному набору собственных функций волновода или мод(их также называютсобственными волнами волновода). Рассмотрим некоторые эвристические соображения, которые приводят к пониманию причин возникновения волноводных мод.

2.1.1. Направляемые моды. Направляемые моды планарного световода. В предыдущей главе мы уже вводили понятие направляемых мод, подразумевая под ними плоские волны, поставленные в соответствие пучкам параллельных направляемых лучей.

Рис.2.1. Интерференция плоских волн в планарном волноводе

Такая трактовка понятия моды и представленная интерпретация ее фазовых параметров весьма наглядны и в некоторых случаях продуктивны, например, при анализе в рамках лучевой модели явления внутримодовой дисперсии. Однако понятие о модах как об однородных плоских волнах, строго говоря, не является корректным. В общем случае, волноводные моды являются сложными электромагнитными волнами, специфичными для геометрии данного световода. Представление о них можно получить, рассматривая результат когерентного сложения нескольких направляемых плоских волн волновода, распространяющихся с одинаковой фазовой скоростью. Поясним на примере планарного волновода. Предположим, что такой волновод направляет две плоские волны, обладающие одинаковой поляризацией и длиной волны. Пусть волновой вектор одной из них ориентирован под углом+, а другой-к оси, так как это показано на рис.2.1. Такие волны, согласно выражению (1.3.1), имеют одинаковую константу распространения и потому их фазовые скорости равны. Для определенности будем полагать, что волны также имеют одинаковые амплитуды, а векторы напряженности их электрических полей направлены перпендикулярно плоскости чертежа, к наблюдателю. Тогда напряженность суммарного электрического поля волн может быть рассчитана в виде:

, (2.1.2)

где E₀- амплитуда электрического поля волн;- единичный вектор в направлении декартовой осиY;и- соответственно волновые вектора первой и второй волны с декартовыми компонентами:и,=(x, y, z) – радиус-вектор точки наблюдения.

После элементарных преобразований выражения (2.1.2) получаем

И окончательно имеем следующее выражение для напряженности суммарного поля волн

. (2.1.3)

Из полученного выражения следует, что в поперечном сечении волновода устанавливается стационарное распределение электрического поля с амплитудой, распределенной по закону

А(х)=. (2.1.4)

В продольном направлении суммарная волна движется с фазовой скоростью v==c, как и каждая из плоских волн в отдельности (см. выражение 1.3.7).

Если предположить, что в процессе полного внутреннего отражения направляемое излучение совершенно не проникает в оболочку, то на границе сердцевины и оболочки амплитуда суммарной волны А(х) должна становиться равной нулю. Этому условию отвечают не любые распределения вида (2.1.4), а только те, для которых поперечный фазовый параметрU принимает значенияm+/2, гдеm– целое число. Последнее означает, что в поперечном сечении волновода могут возбуждаться не любые суммарные волны, а только те из них, которые обладают указанными резонансными значениями поперечного фазового параметра. Собственно, такие волны и представляют направляемые моды волновода

В реальном волноводе при отражении от границы раздела сред световое поле проникает в оболочку на некоторую ненулевую глубину. Поэтому предположение об обнулении амплитуды моды на границе раздела сред не является, строго говоря, верным. Математически это приводит к усложнению выражений для распределения амплитуды поля А(х)и для фазовых параметров мод. Они будут получены далее исходя из решения уравнений Максвелла. Однако предварительный вывод о существовании в волноводе строго определенного дискретного набора направляемых мод остается справедливым.

Рассмотрим теперь напряженность магнитного поля моды, полученной при сложении плоских волн в планарном волноводе. Как видно из рис.2.1 она может быть вычислена в виде.

(2.1.5)

где ,- соответственно векторные амплитуды первой и второй плоской волны с декартовыми компонентами: для первой=(-H_0X,0,-H_0Z), для второй=(-H_0X, 0,H_0Z). После несложных преобразований в выражении (2.1.5) получаем

(2.1.6)

где ,- единичные вектора в направлении декартовых осейX иZсоответственно. Как видно, вектор напряженности магнитного поля суммарной волны имеет одновременно проекции на осиХиZ. В отличие от него вектор напряженности электрического поля этой моды имеет единственную проекцию – на поперечную осьY (см. выражение 1.8), вследствие чего рассматриваемая мода называетсяпоперечной электрической, илиTE (transversal electrical) модой.

Все вышеприведенные рассуждения можно повторить для случая иной поляризации обеих интерферирующих плоских волн, когда векторы их электрического поля лежат в плоскости чертежа на рис.2.1, а векторы напряженности магнитного поля перпендикулярны ей. В этом случае вектор суммарной волны будет иметь две проекции: на осиХиZ, а вектор– только одну поперечную декартову компоненту. Поэтому соответствующая мода называетсяпоперечной магнитной, или TM(transversal magnetical) модой.

2.1.2. Излучательные моды. Процедура сложения плоских волн, подобная рассмотренной выше, может быть проделана для волн, соответствующих рефрагирующим лучам. В результате могут быть получены моды, которые не будут удерживаться сердцевиной волновода, энергия которых постепенно излучается в оболочку. Такие моды называютсяизлучательными. Поскольку на глубину проникновения излучательных мод в оболочку не накладывается никаких ограничений, постоянная распространения таких мод может принимать любые значения внутри диапазона определенного в рамках лучевого анализа: от0доkn₂. Это означает, что излучательные моды в отличие от направляемых, образуют не дискретный, анепрерывный спектр.

2.1.3. Моды оболочки. Световое излучение попадает в оболочку через входной торец, при возбуждении световода, а также из сердцевины вместе с рефрагирующими лучами. Это излучение формирует моды оболочки.

В общем случае для описания электромагнитного поля в волноводе требуется использования мод всех типов: направляемых, излучательных и мод оболочки. Однако принимая во внимание, что излучательные моды и моды оболочки не участвуют в передаче оптических сигналов и достаточно быстро затухают, в дальнейшем будем уделять основное внимание именно направляемым модам волноводов.

2.1.4. Моды волоконных световодов. В волноводах с более сложной геометрией, чем у планарного, часто не представляется возможным получить явные выражения для полей мод методом когерентного сложения плоских волн. В частности, это справедливо для круглого волоконного световода. Поэтому детальное описание собственных волн такого световода будет получено далее с использованием методов, основанных на решении уравнений Максвелла. Здесь отметим только очевидные свойства мод волоконного световода, вытекающие из его геометрических особенностей и лучевых представлений. Так, поля мод волоконного световода будут обладать цилиндрической симметрией как и сам волновод. Причем моды ТE илиТМтипов могут быть поставлены в соответствие толькомеридиональнымлучам. В случаекосыхлучей вектораисоответствующих им волн имеют одновременно ненулевые проекции на продольную ось. Поэтому моды, получаемые при когерентном сложении таких волн, никогда не являются поперечными. Они называются гибридными и обозначаются какНЕиЕН(вторая буква в обозначении мод волоконного световода указывает на доминирующее продольное поле, хотя такое деление в значительной степени условно.)

2.1.5. Скалярное приближение. В слабонаправляющих волноводах углы распространения направляемых лучей весьма малы. Это означает, что векторсоответствующих плоских волн ориентирован практически параллельно оптической оси волновода, а вектораиэтих волн имеют очень малые проекции на эту ось, поэтому моды слабонаправляющих волноводов могут быть сконструированы из почти поперечных плоских волн. Вследствие этого сами моды можно считать почти поперечными. Если полностью пренебречь продольными проекциями векторови, получим моды, которые будут приближенно описывать процессы распространения светового излучения по оптическим волноводам. В случае планарных волноводов, такие собственные волны принято обозначать какТЕМ (transversal electromagnetical)моды, а в случае волоконных световодов их принято обозначать какLP(linearly polarized) моды. Несмотря на различие названий, оба типа мод иТЕМ иLPсчитаются линейно поляризованными поперечными волнами. При необходимости задать иную, отличную от линейной, поляризацию световой волны, например круговую или эллиптическую, ее представляют в виде суперпозиции ортогонально поляризованныхТЕМилиLPмод.

Описание светового поля в волноводе на основе ТЕМилиLPмод носит название скалярного приближения. Такое название связано с тем, что каждый из векторовилюбой линейно поляризованнойТЕМилиLPволны полностью описывается скалярной величиной – проекцией вектора поперечную декартовую ось. Другое название этого приближения – приближение свободного пространства. Последнее связано с тем, что именно в свободном пространстве электромагнитные волны являются чисто поперечными. Иными словами, в рамках скалярного приближения волновод рассматривают как однородную среду, пренебрегая малым изменением показателя преломления на границе между сердцевиной и оболочкой.

Скалярное приближение позволяет значительно упростить решение уравнений Максвелла для оптических волноводов. Действительно, в его рамках число скалярных уравнений в системе (2.1.1) сокращается до четырех:

- для пары проекций Е_ХиН_Y

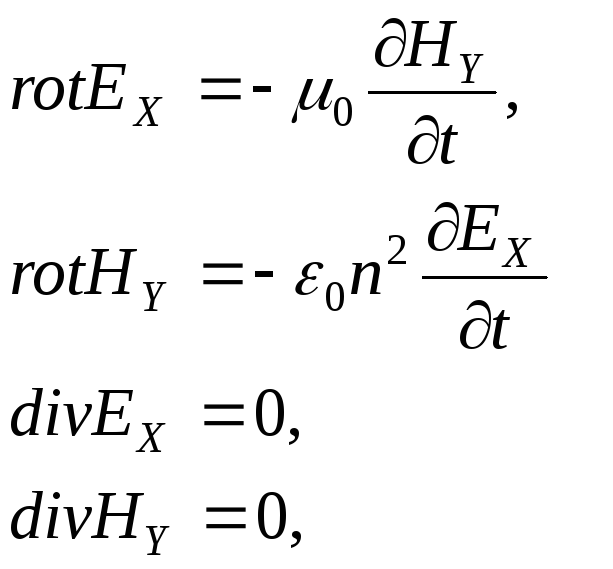(2.1.7)

для света поляризованного вдоль оси Х;

- или для пары Е_Y,Н_X– для света поляризованного вдоль осиY.

Так же, как и в случае скалярных волн свободного пространства [1], к первому уравнению в системе (2.1.4) можно применить операцию ротора. Затем с использованием второго и третьего уравнений, учитывая, что rot rot = grad div - (где=gradgrad- оператор Лапласа), получим стандартное волновое уравнение для электрической компоненты поля [1]:

, (2.1.8)

где Т– означает любую из поперечных осейXилиY. Уравнение (2.1.8) также в неявном виде задает напряженность магнитного поля, поскольку последняя может быть вычислена по найденным из (2.1.8) значениямE_T(x,y,z,t)c помощью 2-го уравнения системы (2.1.7).

В соответствие с предварительными выводами, полученными в разделе 2.1.I, будем искать решение уравнения (2.1.8) в виде волны, распространяющейся вдоль осиZс фазовой скоростью/ и некоторым стационарным распределением амплитуды по поперечному сечению волновода. Сказанное можно математически представить в виде

. (2.1.9).

При подстановке выражения (2.1.9) в (2.1.8) получаем следующее соотношение:

, (2.1.10)

где _T=д²/дx²+д²/дy²- оператор Лапласа в плоскостиХОY поперечного сечения волновода,(x,y)=.

В сердцевине волновода ступенчатого профиля n(x,y)=n₁, и, как это видно из выражения (1.3.3),(x,y)=U/. В оболочке, гдеn(x,y)=n₂и>kn₂, величина (x,y)становится мнимой, как это следует из соотношений (1.3.2) и (1.3.3). Чтобы в дальнейшем избегать в выражении (2.1.10) записи мнимых чисел, введем действительный, положительный параметр

W=, (2.1.11)

который называется поперечным фазовым параметром в оболочке. Последний, как следует из выражений (1.3.3) и (2.1.11), связан с величинамиU, иVследующим соотношением

V=. (2.1.12)

С его использованием величина (x,y)может быть представлена в оболочке как(x,y)=iW/, а выражение (2.1.10) переписано в следующем виде:

в сердцевине волновода ;

(2.1.13)

в оболочке .

Как видно из соотношений (2.1.13), поле моды в оболочке волновода описывается иным дифференциальным уравнением, чем в сердцевине и, следовательно, имеет иной характер. Это понятно и из физических соображений: световое поле направляемой волны должно концентрироваться в сердцевине световода, а при проникновении в оболочку - быстро убывать.

Традиционно для системы уравнений вида (2.1.13) вводится требования «сшивки» решений на границе раздела сред, то есть неразрывности функции А(х,у) и ее первых производных на границе раздела сердцевины и оболочки[5, 6, 12-13]. Система уравнений (2.1.13) с наложенными на ее решения условиями «сшивки» описывает задачу о распределении полей мод в поперечном сечении световода. Дальнейшее рассмотрение такой задачи будет проводиться с учетом геометрии волновода.