3.2. Линейные операции над векторами

С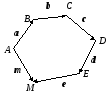уммой векторов а и b называется такой вектор с, начало которого совпадает с началом вектора а, а конец – с концом вектора b, при условии, что начало вектора b приложено к концу вектора а (правило треугольника) (рис. 19, а).

а б в

Рис. 19

Если на векторах а и b, исходящих из одной точки А, построить параллелограмм АВСD (АВ = а; АD = b), то диагональ, исходящая из общего начала векторов а и b, является суммой векторов: АС = а + b (правило параллелограмма) (рис. 19, б).

Разностью векторов а – b называется сумма векторов а и – b. Это другая диагональ параллелограмма: DВ = а – b (рис. 19, б).

Сумма нескольких векторов а, в, с, d, е есть вектор представляющий собой замыкающуюломанойАВСDЕМ, составленной из слагаемых векторов . Сложение векторов может быть выполнено последовательно: конец одного из векторов совпадает с началом другого; коней другого – с началом третьего и т. д., что понятно из рис. 19,в.

Произведением скаляра λ на вектор а называется вектор λа, коллинеарный с вектором а; длина его равна а направление совпадает с направлениема при λ > 0 и противоположно ему при λ < 0.

Линейной комбинацией векторов а, в, …, d со скалярными коэффициентами λ₁, λ₂, …, λ_k называется вектор Любой вектора может быть единственным образом представлен в виде линейной комбинации трех некомпланарных векторов р, q, r:

Координаты вектора. Если i, j, k – орты, то любой вектор АВ = а в пространстве может быть единственным образом представлен в виде линейной комбинации векторов i, j, k (они некомпланарны), следующим образом: при этом скаляры,,называютсяпрямоугольными декартовыми координатами вектора а в системе i, j, k.

Свойства линейных операций над векторами

Если а, в, с – векторы, α и β – скаляры, то:

● ● ●

● ● ●

3.3. Проекции вектора на ось

Проекцией точки М на ось l будем называть основание А перпендику-

куляраМА на ось l. Проекцией вектора на осьl называется длина отрезка АВ, где точка А – проекция начала, а точка В – проекция конца вектора а на ось l. Обозначение: .

Основные теоремы о проекциях векторов:

1. Проекция вектора на какую-либо ось равна произведению модуля вектора на косинус угла наклона вектора к оси:

2. Проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на эту же ось.

3. При умножении вектора на скаляр его проекция умножается на тот же скаляр.

Проекции точки М на оси координат Ох, Оу, Оz называются координатами этой точки и обозначаются Прямоугольные декартовы координаты вектора являются проекциями этого вектора на осиОх, Оу, Оz. Это обозначается так:

Если известны координаты начала и концавектораАВ = а, то чтобы найти проекции (координаты) вектора, надо из координат конца вычесть соответствующие координаты начала (рис. 20), т. е.

Рис. 20

3.4. Направляющие косинусы вектора. Модуль вектора

Направляющие косинусы вектора – это косинусы углов α, β, γ, которые вектор образует с положительными направлениями осей координат. Пусть дан вектор (рис. 21). Тогда направляющие косинусы вектораа можно найти по формулам:

где длина (модуль) вектора определя-ется по формуле:

Следствие. Сумма квадратов направляющих косинусов равна единице.