Экзаменационный билет № 07

1. Смешанная задача для однородного волнового уравнения на отрезке 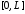при нулевых граничных условиях.

2. Формула Бернулли (с доказательством).

3. Решить задачу Дирихле для уравнения Лапласа в кольце.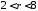

ГУ: .

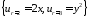4. Случайная величина задана плотностью вероятностиопределить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

1. Смешанная задача для однородного волнового уравнения на отрезке 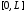при нулевых граничных условиях имеет вид:

, ,,

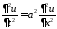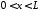граничные условия: ;

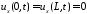начальные условия: ,.

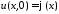Для решения задачи воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения 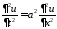будем искать в вид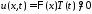е. Подставляем в уравнение и разделяем переменные:

, ,

: ,

, ,.

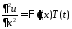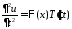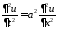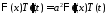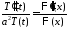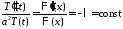Тогда функции и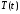являются соответственно решениями уравнений

, .

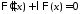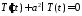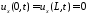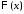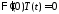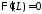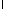Из граничных условий получаем краевые условия для функции:,, значит,,. Таким образом, для определенияиполучаем задачу Штурма-Лиувилля

: ,

, .

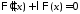
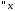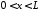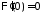Поскольку мы имеем дело со второй краевой задачей, то 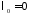является собственным значением, а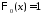– соответствующей ему собственной функцией.

Пусть теперь 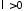(при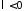задача имеет только тривиальные решения). Общее решение уравнения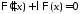имеет вид

.

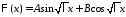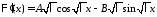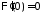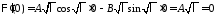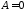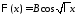Тогда . Из краевого условияполучаем:,, т.е.и.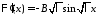

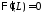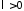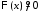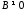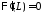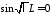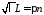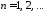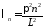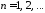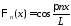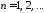Из краевого условия получаем:. Посколькуи, тои равенствовозможно тогда и только тогда, когда, откуда получаем,, т.е.,. Тогда получим,. Таким образом, получили решение задачи Штурма-Лиувилля:

собственные значения ,,;

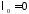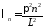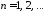собственные функции ,,.

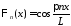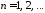Теперь при каждом 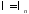решаем уравнение для:

, .

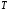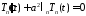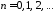При 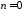получим уравнение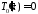, откуда

.

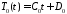При 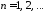общее решение этого уравнения имеет вид

.

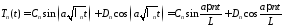Тогда

.

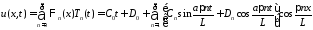Для нахождения коэффициентов 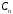,,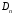, воспользуемся начальными условиями,.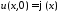

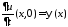Разложим функции и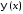на отрезкев ряды Фурье по системе: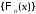

,

,

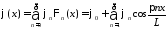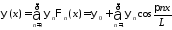где

,

,

,

,

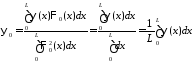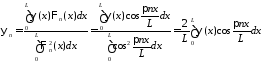так как .

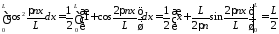Тогда начальное условие 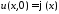дает

,

откуда

, .

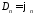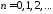Находим :

.

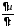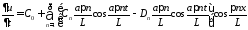Тогда начальное условие дает

,

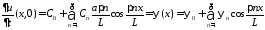откуда

, ,,.

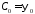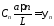Тогда решением задачи является ряд

.

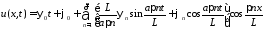2. Схемой Бернулли (или последовательностью независимых испытаний) называют последовательность испытаний, удовлетворяющую условиям:

1) в каждом испытании возможны лишь два исхода – появление некоторого события (которое мы будем называть "успехом") или его не появление, т.е. осуществление события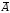(в этом случае мы будем говорить, что испытание закончилось "неудачей");

2) испытания являются независимыми, т.е. исход -го испытания не зависит от исходов всех предыдущих испытаний;

3) вероятность успеха во всех испытаниях постоянна и равна .

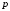Вероятность неудачи в каждом испытании обозначим через :.

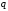При рассмотрении схемы Бернулли основной задачей является нахождение вероятности события, состоящего в том, что в испытаниях успех появится ровнораз,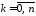. Обозначим эту вероятность через.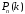

Теорема. Вероятность того, что виспытаниях по схеме Бернулли произойдет ровно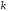успехов, определяется формулой Бернулли

, .

Доказательство. Обозначим событие "появление успеха" через У, а событие "появление неудачи" через Н. Тогда элементарными исходами последовательности из независимых испытаний будут всевозможные цепочки длины, состоящие из событий У и Н. Всего существует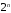различных цепочек такого вида. Посчитаем вероятности элементарных исходов. В силу независимости испытаний события У, Н, Н, ..., У, У являются независимыми и согласно теореме умножения вероятность того, что виспытаниях успех появился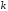раз, равна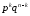,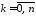. Поскольку всего существуетспособов расположить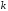«успехов» средииспытаний, то.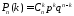

3. Задача Дирихле для уравнения Лапласа в кольце 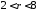ставится следующим образом:

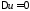при ,

,

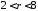где 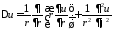– оператор Лапласа в полярных координатах,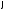(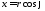,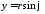). Граничные условия преобразуем в полярные координаты:

, .

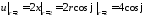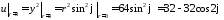Из условия однозначности решения вытекает условие периодичности

.

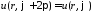Для нахождения решения этой задачи используем метод Фурье.

Нетривиальные решения уравнения 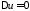будем искать в виде

,

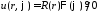Подставляем 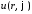в уравнение и разделяем переменные:

,

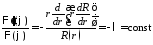откуда

,

.

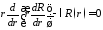Из условия периодичности следует, что

, .

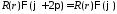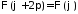Таким образом, для получаем задачу на собственные значения

,

.

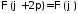Если 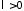, то

.

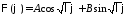Применяем условие периодичности:

.

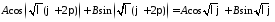Отсюда, ,,.

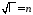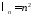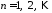Если 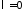, то

.

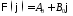Следует взять 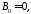иначе не выполнится условие периодичности.

При 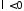ненулевых периодических решений нет.

Окончательно имеем

, .

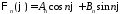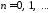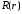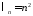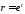Чтобы решить уравнение для при, сделаем замену. Получим

, ,

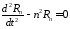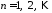откуда

,

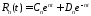т.е.

, .

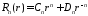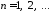При 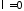получим.

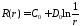Таким образом, функции

,

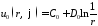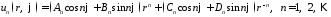
являются частными решениями уравнения 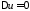. Составим функцию

,

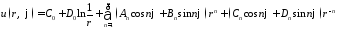которая вследствие линейности и однородности уравнения Лапласа также будет его решением.

Для нахождения 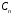,,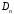, 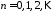воспользуемся граничными условиями.

Из условия 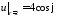имеем:

,

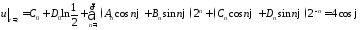откуда

, ,,

, ,

,

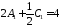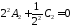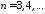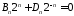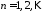
Из условия 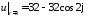имеем:

,

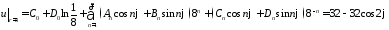откуда

, ,,

, ,

,

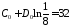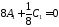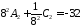Из системы

, ,

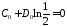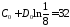находим ,.

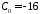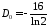Из системы

, ,

находим ,.

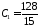Из системы

, ,

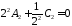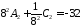находим ,.

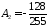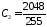Из систем

, ,,

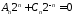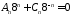находим ,,.

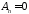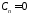Из систем

, ,,

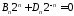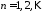находим ,,.

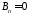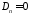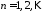Тогда в ряде для 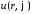ненулевыми являются только коэффициенты

, ,,,,.

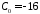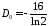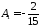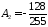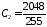Окончательно решение заданной задачи Дирихле для уравнения Лапласа в кольце имеет вид

.

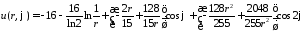4. Математическое ожидание и дисперсию найдем соответственно по формулам:

, .

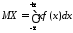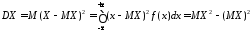Для заданной плотности имеем:

,

.

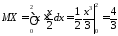Среднеквадратическое отклонение равно:

.
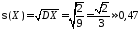