
- •Экзаменационный билет № 01
- •Экзаменационный билет № 02
- •Экзаменационный билет № 03
- •Экзаменационный билет № 04
- •Экзаменационный билет № 05
- •Экзаменационный билет № 06
- •Экзаменационный билет № 07
- •Экзаменационный билет № 08
- •Экзаменационный билет № 09
- •Экзаменационный билет № 10
- •Экзаменационный билет № 11
- •Экзаменационный билет № 12
- •Экзаменационный билет № 13
- •Экзаменационный билет № 14
- •Экзаменационный билет № 15
- •Экзаменационный билет № 16
- •Экзаменационный билет № 17
- •Экзаменационный билет № 18
- •Экзаменационный билет № 19
- •Экзаменационный билет № 20
Экзаменационный билет № 08
1.
Смешанная задача для однородного
волнового уравнения на отрезке
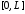 при нулевых граничных условиях
при нулевых граничных условиях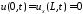 .
.
2.
Нормальный закон распределения. Доказать,
что, если
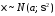 ,
то
,
то .
.
3. Найти решение смешанной задачи для волнового уравнения на полупрямой
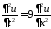 ,
,
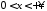 ,
,
ГУ:
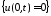 ;
;
НУ:
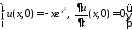 .
.
4. Из 100 лампочек 20 изготовлены на первом заводе, 30 на втором, а остальные на третьем. Первый завод выпускает 1% брака, второй – 0,5%; третий – 0,6%. Какова вероятность того, что наудачу взятая лампочка окажется бракованной?
1.
Смешанная задача для однородного
волнового уравнения на отрезке
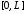 при нулевых граничных условиях имеет
вид:
при нулевых граничных условиях имеет
вид:
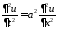 ,
,
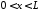 ,
,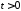 ,
,
граничные
условия:
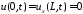 ;
;
начальные
условия:
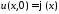 ,
,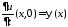 .
.
Для
решения задачи воспользуемся методом
Фурье (разделения переменных). Нетривиальные
решения уравнения
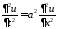 будем искать в виде
будем искать в виде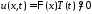 .
Подставляем в уравнение и разделяем
переменные:
.
Подставляем в уравнение и разделяем
переменные:
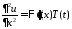 ,
,
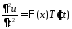 ,
,
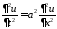 :
:
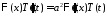 ,
,
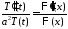 ,
,
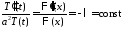 ,
,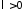 .
.
Тогда
функции
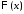 и
и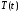 являются соответственно решениями
уравнений
являются соответственно решениями
уравнений
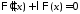 ,
,
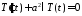 .
.
Из
граничных условий
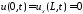 получаем краевые условия для функции
получаем краевые условия для функции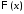 :
: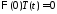 ,
,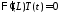 ,
значит,
,
значит,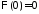 ,
,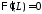 .
Таким образом, для определения
.
Таким образом, для определения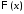 и
и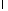 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
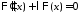
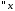 :
:
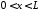 ,
,
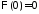 ,
,
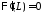 .
.
При
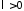 (при
(при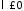 задача имеет только тривиальные решения)
общее решение уравнения
задача имеет только тривиальные решения)
общее решение уравнения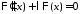 имеет вид
имеет вид
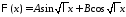 .
.
Из
краевого условия
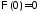 получаем:
получаем: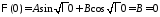 ,
,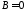 ,
т.е.
,
т.е.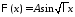 и
и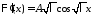 .
.
Из
краевого условия
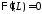 получаем:
получаем: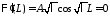 .
Поскольку
.
Поскольку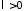 и
и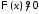 ,
то
,
то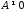 и равенство
и равенство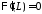 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда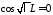 ,
откуда получаем
,
откуда получаем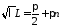 ,
,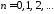 ,
т.е.
,
т.е.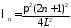 ,
,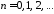 .
Тогда получим
.
Тогда получим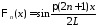 ,
,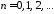 .
Таким образом, получили решение задачи
Штурма-Лиувилля:
.
Таким образом, получили решение задачи
Штурма-Лиувилля:
собственные
значения
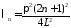 ,
,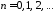 ;
;
собственные
функции
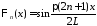 ,
,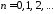 .
.
Теперь
при каждом
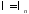 решаем уравнение для
решаем уравнение для :
:
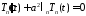 ,
,
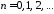 .
.
Общее решение этого уравнения имеет вид
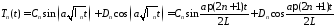 .
.
Тогда
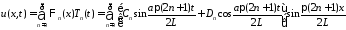 .
.
Для
нахождения коэффициентов
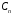 ,
,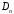 ,
,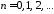 ,
воспользуемся начальными условиями
,
воспользуемся начальными условиями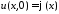 ,
,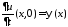 .
.
Разложим
функции
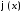 и
и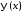 на отрезке
на отрезке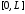 в ряды Фурье по системе
в ряды Фурье по системе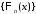 :
:
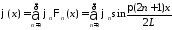 ,
,
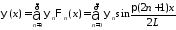 ,
,
где
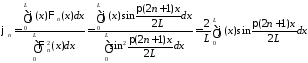 ,
,
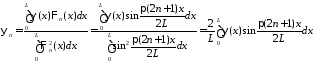 ,
,
так как
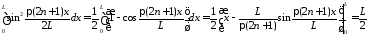 .
.
Тогда
начальное условие
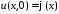 дает
дает
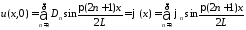 ,
,
откуда
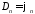 ,
,
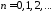 .
.
Находим
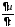 :
:
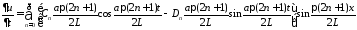 .
.
Тогда
начальное условие
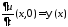 дает
дает
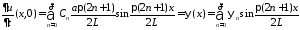 ,
,
откуда
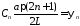 ,
,
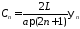 ,
,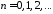 .
.
Тогда решением задачи является ряд
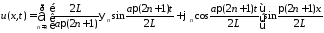 .
.
2.
Нормальным распределением с параметрами
 ,
,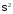 называется распределение вероятностей
с плотностью (
называется распределение вероятностей
с плотностью (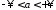 ,
,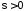 )
)
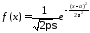 ,
,
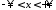 .
.
Математическое
ожидание непрерывной случайной величины
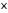 находится по формуле
находится по формуле
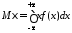 .
.
Для нормального закона
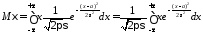 .
.
Сделаем
в интеграле замену
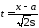 ,
откуда
,
откуда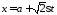 ,
,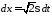 ,
если
,
если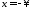 ,
то
,
то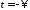 ,
если
,
если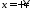 ,
то
,
то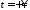 .
Тогда
.
Тогда
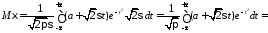
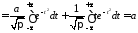 ,
,
так как
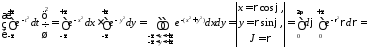
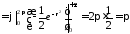 ,
,
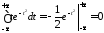 .
.
3. Для смешанной задачи для волнового уравнения на полупрямой
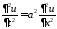 ,
,
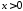 ,
,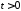 ,
,
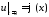 ,
,
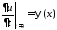 ,
,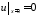 .
.
решение записывается по формуле Даламбера
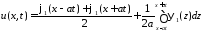 ,
,
где
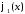 ,
,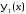 продолженные нечётным образом на
отрицательную часть оси
продолженные нечётным образом на
отрицательную часть оси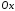 функции
функции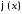 и
и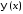 соответственно, то есть:
соответственно, то есть:
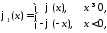
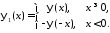
У
нас
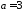 ,
,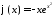 ,
,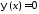 .
Тогда
.
Тогда
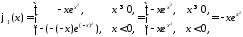 ,
,
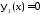
и решение задачи имеет вид
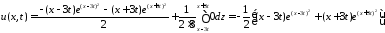 .
.
4. Воспользуемся формулой полной вероятности. Событие
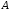 –наудачу
взятая лампочка оказалась бракованной.
–наудачу
взятая лампочка оказалась бракованной.
Введем гипотезы:
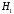 –лампочка
произведена на первом заводе;
–лампочка
произведена на первом заводе;
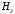 –лампочка
произведена на втором заводе;
–лампочка
произведена на втором заводе;
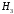 –лампочка
произведена на третьем заводе.
–лампочка
произведена на третьем заводе.
Поскольку всего изготовлено 100 лампочек, то вероятности гипотез
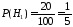 ,
,
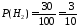 ,
,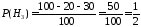 .
.
Условные
вероятности
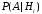 ,
,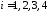 ,
по условию равны
,
по условию равны
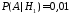 ,
,
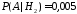 ,
,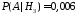 .
.
Тогда по формуле полной вероятности
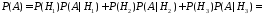
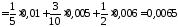 .
.
Экзаменационный билет № 09
1. Уравнение теплопроводности. Задача Коши для уравнения теплопроводности на всей прямой. Формула Пуассона.
2. Дисперсия случайной величины, свойства. Вывести формулу для нахождения дисперсии случайной величины, подчиненной биномиальному закону распределения вероятностей.
3. Решить задачу Коши для неоднородного волнового уравнения
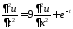 ,
,
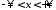 ,
,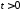 ,
,
НУ:
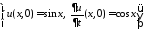 .
.
4. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами 5 см и (0,9 см)2. Найти вероятность того, что отклонение диаметра наудачу взятой детали от её математического ожидания будет меньше 2 см.
1. Уравнение теплопроводности имеет вид:
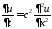 ,
,
где
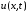 – температура тела в точке
– температура тела в точке в момент времени
в момент времени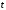 ,
,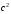 – коэффициент температуропроводности.
– коэффициент температуропроводности.
Задача Коши для уравнения теплопроводности на всей прямой имеет вид
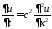 ,
,
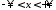 ,
,
начальное
условие:
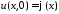 – температура в начальный момент
времени.
– температура в начальный момент
времени.
Получим
её решение. Возьмем
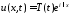 .
Тогда
.
Тогда
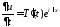 ,
,
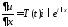 ,
,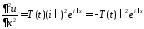 .
.
Подставив в уравнение, получим
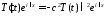 ,
,
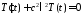 ,
,
откуда
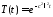 .
Тогда
.
Тогда
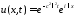 ,
,
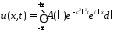 .
.
При
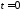 получим
получим
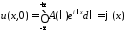 .
.
С помощью обратного преобразования Фурье
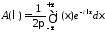 .
.
Тогда
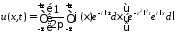 .
.
Меняя порядок интегрирования, получим
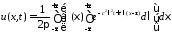
Приведем
экспоненту к виду
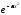 :
:
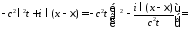
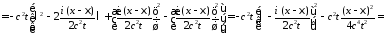
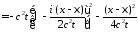 .
.
Тогда
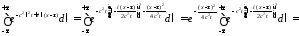
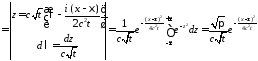 ,
,
так как
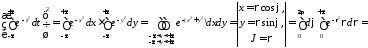
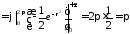 .
.
Значит,
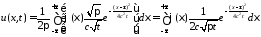 .
.
Обозначим
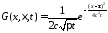 .
.
Тогда получим формулу Пуассона, которая дает решение задачи Коши для уравнения теплопроводности на всей прямой:
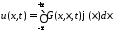 .
.
2.
Определение. Дисперсией
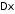 случайной величины
случайной величины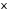 называется математическое ожидание
квадрата отклонения от
называется математическое ожидание
квадрата отклонения от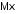 :
:
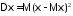 .
.
Дисперсия служит мерой рассеяния значений случайной величины около среднего значения (математического ожидания).
Свойства дисперсии:
1)
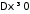 ;
;
2)
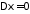 тогда и только тогда, когда
тогда и только тогда, когда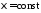 ;
;
3)
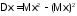 ;
;
4)
для любых
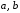
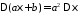 ;
;
5)
если случайные величины
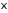 и
и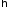 независимы, то
независимы, то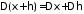 .
.
Докажем свойство 3):
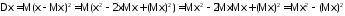 .
.
Для дискретных и непрерывных случайных величин дисперсия вычисляется соответственно по формулам:
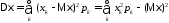 ,
,
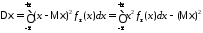 .
.
Найдем
дисперсию биномиального распределения.
Пусть случайная величина
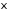 имеет биномиальное распределение, т.е.
она принимает значения от 0 до
имеет биномиальное распределение, т.е.
она принимает значения от 0 до с вероятностями
с вероятностями
 ,
,
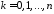 ,
,
и
является числом успехов в
 испытаниях по схеме Бернулли с вероятностью
успеха
испытаниях по схеме Бернулли с вероятностью
успеха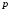 ,
,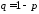 .
Рассмотрим
.
Рассмотрим бернуллиевых случайных величин
бернуллиевых случайных величин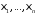 ,
которые принимают два значения: 1 с
вероятностью
,
которые принимают два значения: 1 с
вероятностью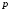 ,
если соответствующее испытание
закончилось успехом, и 0 с вероятностью
,
если соответствующее испытание
закончилось успехом, и 0 с вероятностью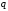 в противном случае. Тогда
в противном случае. Тогда
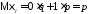 ,
,
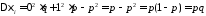 ,
,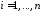 .
.
Кроме
того,
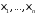 независимы и
независимы и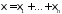 .
Значит, по свойству 5) дисперсии дисперсия
биномиального распределения равна
.
Значит, по свойству 5) дисперсии дисперсия
биномиального распределения равна
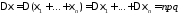 .
.
3. Решение задачи Коши для неоднородного волнового уравнения
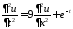 ,
,
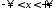 ,
,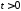 ,
,
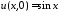 ,
,
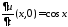 ,
,
будем искать в виде
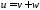 ,
,
где
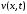 – решение задачи
– решение задачи
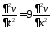 ,
,
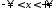 ,
,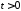 ,
,
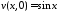 ,
,
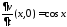 ,
,
а
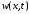 – решение задачи
– решение задачи
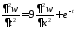 ,
,
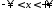 ,
,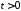 ,
,
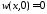 ,
,
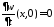 .
.
Функцию
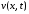 находим по формуле Даламбера
находим по формуле Даламбера
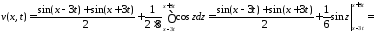
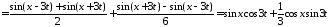 .
.
Функция
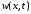 находится по формуле
находится по формуле
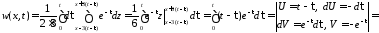
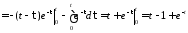 .
.
Тогда
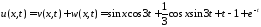 .
.
4.
Для расчета вероятностей попадания
нормальной случайной величины
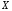 с математическим ожиданием
с математическим ожиданием и среднеквадратическим отклонением
и среднеквадратическим отклонением в промежуток
в промежуток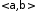 используется формула
используется формула
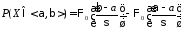 ,
,
где
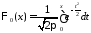 ,
причем
,
причем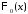 – нечетная функция:
– нечетная функция: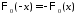 .
.
Пусть
случайная величина
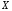 – размер диаметра детали. При
– размер диаметра детали. При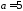 ,
,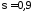 получим
получим
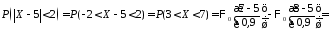
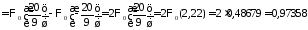 .
.
