Экзаменационный билет № 06

1. Смешанная задача для неоднородного волнового уравнения на отрезке при нулевых граничных условиях.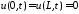

2. Формула Пуассона (с доказательством).

3. Решить задачу Дирихле для уравнения Лапласа 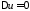вне круга радиуса. ГУ:.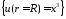

4. Найти математическое ожидание и дисперсию числа выпадений герба при десяти подбрасываниях монеты.

1. Смешанная задача для неоднородного волнового уравнения на отрезке 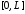при нулевых граничных условиях имеет вид:

, ,,

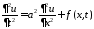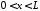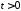граничные условия: ;

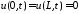начальные условия: ,.

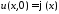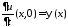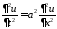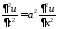Сначала найдем общее решение однородного уравнения при нулевых граничных условиях. Для этого воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнениябудем искать в вид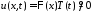е. Подставляем в уравнение и разделяем переменные:

, ,

: ,

, ,.

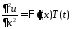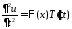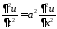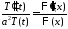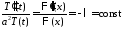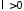Тогда функци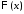и и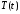являются соответственно решениями уравнений

, .

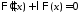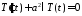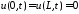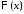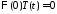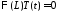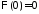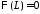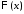Из граничных условий получаем краевые условия для функции:,, значит,,. Таким образом, для определенияи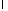получаем задачу Штурма-Лиувилля

: ,

, .

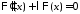
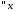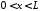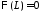Поскольку 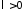(при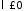задача имеет только тривиальные решения), то общее решение уравненияимеет вид

.

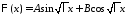Из краевого условия 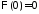получаем: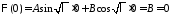, т.е..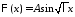

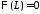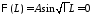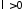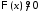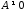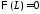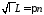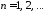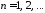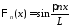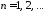Из краевого условия получаем:. Посколькуи, тои равенствовозможно тогда и только тогда, когда, откуда получаем,, т.е.,. Тогда получим,. Таким образом, получили решение задачи Штурма-Лиувилля:

собственные значения ,;

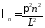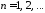собственные функции ,.

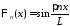Разложим функции 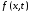,,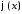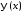в ряды Фурье на отрезке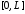по системе собственных функций:

,

,

,

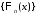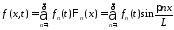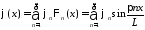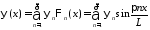где

,

,

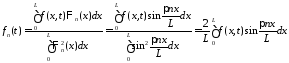
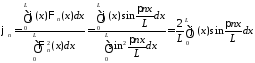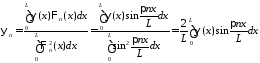так как .

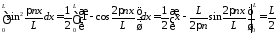Решение смешанной задачи для неоднородного волнового уравнения будем искать в виде ряда

,

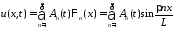где функции 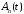,,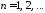 подберем так, чтобы удовлетворить неоднородному уравнению и начальным условиям. Заметим, что функция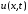при любом выборе функций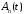,,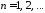 точно удовлетворяет однородным граничным условиям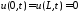. Находим производные

, ,

,

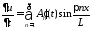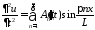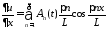и подставляем их в неоднородное уравнение :

,

,

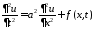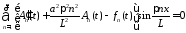откуда получим, что функции 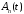,, удовлетворяют уравнениям

.

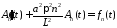Из начальных условий получаем:

,

,

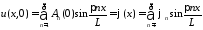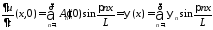откуда

, .

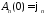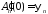Итак, функции 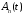,,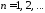 являются решениями задачи Коши

,

, .

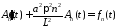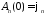Найдем её решение методом вариации. Общее решение соответствующего однородного уравнения 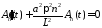имеет вид

.

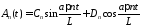Решение неоднородного уравнения будем искать в виде

.

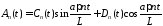Находим :

.

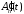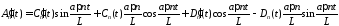Положим

.

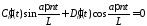Тогда

.

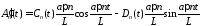Находим :

.

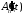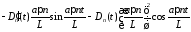Подставляем в уравнение:

,

.

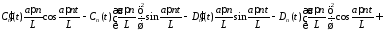
Итак, для определения 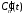и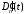получим систему линейных уравнений

,

.

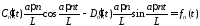Решаем её по формулам Крамера

,

, .

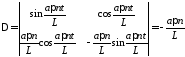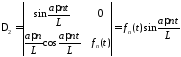Тогда

, .

Из начальных условий 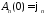,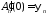получим

,

.

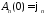
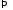
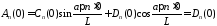
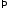
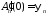
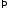
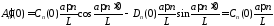
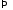
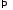
Интегрируя от 0 до 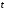, получим

, ,

,

, ,

.

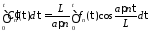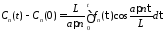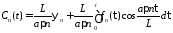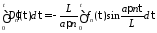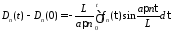Тогда

.

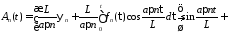
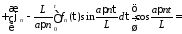
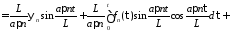
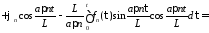
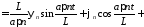
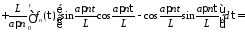
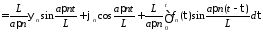Окончательно получим решение смешанной задачи для неоднородного волнового уравнения при нулевых граничных условиях в виде

.

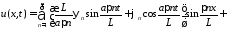
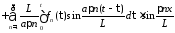2. Теорема Пуассона. Если в схеме Бернулли 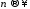,,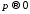 причем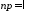, где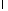– некоторая положительная постоянная (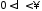), то

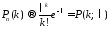
при любом постоянном ,.

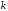Доказательство. Обозначим 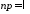. Тогда

.

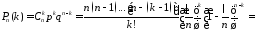
Поскольку постоянно, то все сомножители, начиная с третьего при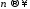стремятся к единице; второй же сомножитель при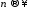стремится к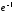(второй замечательный предел). Тогда

.

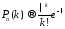Таким образом, если число испытаний по схеме Бернулли велико, а вероятность успеха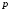в одном испытании достаточно мала, то вероятность того, что виспытаниях успех появится ровно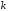раз, может быть приближенно посчитана по формуле

.

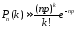3. Внешняя задача Дирихле для уравнения Лапласа вне круга радиуса 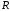ставится следующим образом:

при ,

,

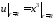где 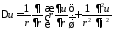– оператор Лапласа в полярных координатах,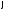(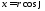,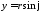). Граничное условие преобразуем в полярные координаты:

.

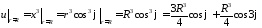Из условия однозначности решения вытекает условие периодичности

.

Для нахождения решения этой задачи используем метод Фурье.

Нетривиальные решения уравнения 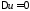будем искать в виде

,

Подставляем 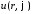в уравнение и разделяем переменные:

,

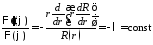откуда

,

.

Из условия периодичности следует, что

, .

Таким образом, для получаем задачу на собственные значения

,

.

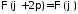Если 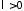, то

.

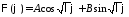Применяем условие периодичности:

.

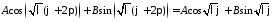Отсюда, ,,.

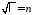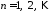Если 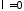, то

.

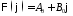Следует взять 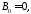иначе не выполнится условие периодичности.

При 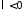ненулевых периодических решений нет.

Окончательно имеем

, .

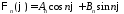Чтобы решить уравнение для при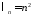, сделаем замену. Получим

, ,

откуда

,

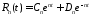т.е.

, .

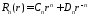При 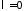получим.

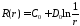Таким образом, функции

,

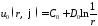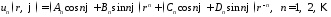
являются частными решениями уравнения 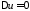. Составим функцию

,

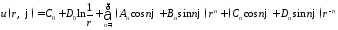которая вследствие линейности и однородности уравнения Лапласа также будет его решением.

Поскольку задача рассматривается во внешности круга радиуса 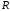, то следует положить равными нулю коэффициенты при частных решениях, которые является неограниченными в области, т.е.

, ,.

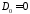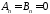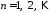Итак, в области 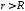имеем

.

Для нахождения 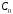,,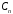,,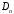 воспользуемся граничным условием: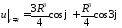

,

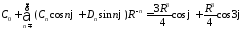откуда

, ,,,,

, .

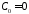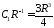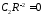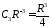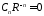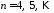
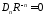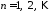Тогда в ряде для 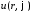ненулевыми являются только коэффициенты

, .

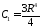По условию 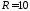, поэтому окончательно решение заданной внешней задачи Дирихле для уравнения Лапласа вне круга имеет вид

.

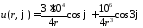4. Здесь мы имеем дело с испытаниями по схеме Бернулли, где «успех» – выпадение герба при подбрасывании монеты, вероятность «успеха» 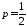, всего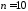испытаний. Случайная величина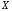– число выпадений герба при десяти подбрасываниях монеты – имеет биномиальное распределение. Поскольку для биномиального распределения

, ,

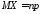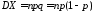то математическое ожидание и дисперсия числа выпадений герба при десяти подбрасываниях монеты равны

, .
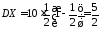