
- •Экзаменационный билет № 01
- •Экзаменационный билет № 02
- •Экзаменационный билет № 03
- •Экзаменационный билет № 04
- •Экзаменационный билет № 05
- •Экзаменационный билет № 06
- •Экзаменационный билет № 07
- •Экзаменационный билет № 08
- •Экзаменационный билет № 09
- •Экзаменационный билет № 10
- •Экзаменационный билет № 11
- •Экзаменационный билет № 12
- •Экзаменационный билет № 13
- •Экзаменационный билет № 14
- •Экзаменационный билет № 15
- •Экзаменационный билет № 16
- •Экзаменационный билет № 17
- •Экзаменационный билет № 18
- •Экзаменационный билет № 19
- •Экзаменационный билет № 20
Экзаменационный билет № 01
1. Задача Коши для одномерного волнового уравнения на всей прямой. Формула Даламбера.
2. Теорема сложения вероятностей (с доказательством). Вероятность противоположного события.
3. Найти решение смешанной задачи
 ,
,
 ,
,
ГУ:
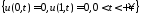 ;
НУ:
;
НУ: .
.
4. В хлопке 75% длинных волокон. Какова вероятность того, что среди взятых наудачу трёх волокон окажутся 2 длинных волокна?
1. Задача Коши для одномерного волнового уравнения на всей прямой имеет вид:
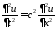 ,
,
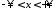 ,
,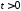 ,
,
начальные
условия:
 ,
, .
.
Решение задачи будем искать в виде суммы прямой и обратной бегущих волн:
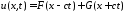 .
.
Воспользуемся
для нахождения функций
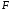 и
и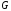 начальными условиями:
начальными условиями:
 :
:
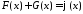 ,
,
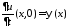 :
:
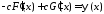 .
.
Интегрируя
уравнение
 в пределах от
в пределах от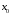 до
до ,
получим
,
получим
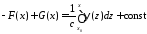 .
.
Тогда из системы
 ,
,
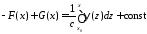 ,
,
находим
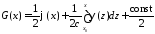 ,
,
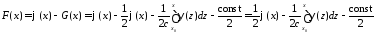 .
.
Значит,
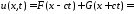

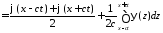 .
.
Итак, решение задачи Коши для одномерного волнового уравнения на всей прямой имеет вид
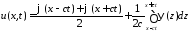 .
.
Это формула Даламбера.
2.
Теорема сложения вероятностей. Если
события
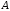 и
и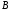 совместны, то
совместны, то
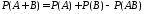 .
.
Доказательство.
Пусть
 – числе всех равновозможных исходов
испытания, в результате которого могут
появиться события
– числе всех равновозможных исходов
испытания, в результате которого могут
появиться события и
и .
Пусть
.
Пусть – число тех исходов, которые благоприятствуют
событию
– число тех исходов, которые благоприятствуют
событию ,
,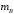 – число тех исходов, которые благоприятствуют
событию
– число тех исходов, которые благоприятствуют
событию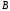 ,
,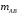 – число тех исходов, которые благоприятствуют
произведению событий
– число тех исходов, которые благоприятствуют
произведению событий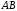 .
Тогда событию
.
Тогда событию благоприятствуют исходы числом
благоприятствуют исходы числом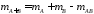 .
Значит, по формуле классической
вероятности
.
Значит, по формуле классической
вероятности
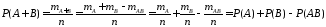 .
.
Следствие.
Если события
 и
и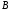 несовместны, то
несовместны, то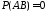 и
и
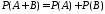 .
.
Для
трех событий
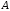 ,
,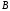 и
и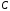 теорема сложения имеет вид
теорема сложения имеет вид
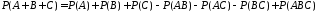 .
.
Для
 событий теорема сложения имеет вид
событий теорема сложения имеет вид

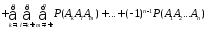 .
.
Противоположные
события
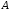 и
и несовместны и в сумме дают достоверное
событие, поэтому
несовместны и в сумме дают достоверное
событие, поэтому
 ,
,
откуда получаем формулу для вероятности противоположного события
 .
.
3.
Для решения задачи воспользуемся методом
Фурье (разделения переменных). Нетривиальные
решения уравнения
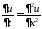 будем искать в виде
будем искать в виде .
Подставляем в уравнение и разделяем
переменные:
.
Подставляем в уравнение и разделяем
переменные:
 ,
,
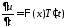 ,
,
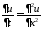 :
:
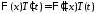 ,
,
 ,
,
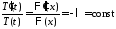 ,
, .
.
Тогда
функции
 и
и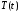 являются соответственно решениями
уравнений
являются соответственно решениями
уравнений
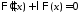 ,
,
 .
.
Из
граничных условий
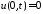 ,
,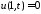 получаем краевые условия для функции
получаем краевые условия для функции :
: ,
, ,
значит,
,
значит, ,
,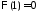 .
Таким образом, для определения
.
Таким образом, для определения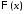 и
и получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
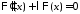
 :
:
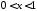 ,
,
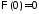 ,
,
 .
.
Поскольку
 (при
(при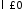 задача имеет только тривиальные решения),
то общее решение уравнения
задача имеет только тривиальные решения),
то общее решение уравнения имеет вид
имеет вид
 .
.
Из
краевого условия
 получаем:
получаем: ,
т.е.
,
т.е. .
.
Из
краевого условия
 получаем:
получаем: .
Поскольку
.
Поскольку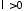 и
и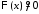 ,
то
,
то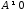 и равенство
и равенство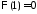 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда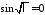 ,
откуда получаем
,
откуда получаем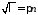 ,
,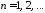 ,
т.е.
,
т.е.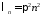 ,
,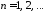 .
Тогда получим
.
Тогда получим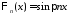 ,
,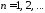 .
Таким образом, получили решение задачи
Штурма-Лиувилля:
.
Таким образом, получили решение задачи
Штурма-Лиувилля:
собственные
значения
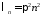 ,
,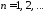 ;
;
собственные
функции
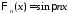 ,
, .
.
Теперь
при каждом
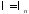 решаем уравнение для
решаем уравнение для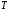 :
:
 ,
,
 .
.
Общее решение этого уравнения имеет вид
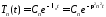 .
.
Тогда
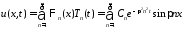 .
.
Для
нахождения коэффициентов
 ,
, ,
воспользуемся начальным условием
,
воспользуемся начальным условием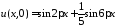 .
.
Начальное
условие
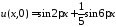 дает
дает
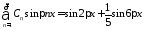 ,
,
откуда
 ,
,
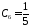 ,
,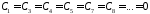 .
.
Тогда решение задачи есть
 .
.
4.
Мы имеем дело с последовательностью
независимых испытаний по схеме Бернулли,
где событие «успех» – появление при
выборе длинного волокна. По условию
вероятность «успеха» равна
 .
Проведено
.
Проведено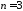 испытаний. Тогда по формуле Бернулли
вероятность того, что «успех» появится
ровно 2 раза (т.е. среди взятых наудачу
трёх волокон окажутся 2 длинных волокна),
равна
испытаний. Тогда по формуле Бернулли
вероятность того, что «успех» появится
ровно 2 раза (т.е. среди взятых наудачу
трёх волокон окажутся 2 длинных волокна),
равна
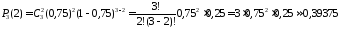 .
.
Экзаменационный билет № 02
1. Задача Коши для неоднородного волнового уравнения на всей прямой.
2. Формула полной вероятности (с доказательством). Формула Байеса.
3. Найти решение смешанной задачи
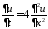 ,
,
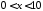 ,
,
ГУ:
 ;
НУ:
;
НУ: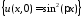 .
.
4.
Плотность вероятности случайной величины
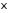 имеет вид
имеет вид ,
, .
Найти вероятность того, что
.
Найти вероятность того, что попадет на
попадет на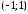 .
.
1. Задача Коши для неоднородного волнового уравнения на всей прямой имеет вид:
 ,
,
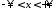 ,
,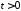 ,
,
начальные
условия:
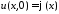 ,
,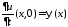 .
.
Для решения этой задачи разобьем её на две:
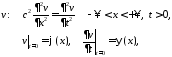
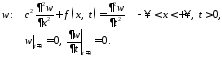
Тогда
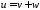 .
Функцию
.
Функцию можно записать по формуле Даламбера
можно записать по формуле Даламбера
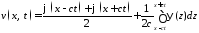 .
.
Для
нахождения
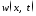 строим вспомогательную задачу
строим вспомогательную задачу
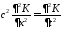
 ,
,
 ,
,
 ,
,
при
этом
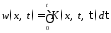 .
.
Функция
 также может быть записана по формуле
Даламбера
также может быть записана по формуле
Даламбера
 ,
,
а потому
 ,
,
и, таким образом,
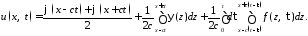
2.
События
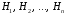 образуют полную группу попарно
несовместных событий, если:
образуют полную группу попарно
несовместных событий, если:
а)
они являются попарно несовместными,
т.е.
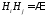 при
при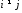 ;
;
б)
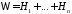 .
.
Теорема.
Пусть
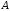 – некоторое событие, а события
– некоторое событие, а события образуют полную группу попарно
несовместных событий. Тогда имеет место
формула полной вероятности
образуют полную группу попарно
несовместных событий. Тогда имеет место
формула полной вероятности
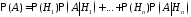 .
.
Доказательство.
Заметим, что событие
 можно представит в виде суммы попарно
несовместных событий (рис.):
можно представит в виде суммы попарно
несовместных событий (рис.):
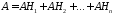 .
.
 Рис.
Рис.
Используя теорему сложения, получим
 .
.
Применяя к слагаемым последней суммы теорему умножения
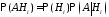 ,
,
получим
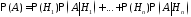 .
.
События
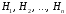 называют гипотезами.
называют гипотезами.
Часто
бывает, что событие
 может происходить при двух взаимоисключающих
условиях
может происходить при двух взаимоисключающих
условиях и
и .
Если
.
Если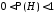 ,
то события
,
то события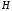 и
и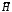 образуют полную группу событий и формулу
полной вероятности можно записать в
виде
образуют полную группу событий и формулу
полной вероятности можно записать в
виде
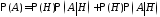 .
.
Теорема.
Пусть события
 удовлетворяют условиям, сформулированным
в условии теоремы о формуле полной
вероятности и
удовлетворяют условиям, сформулированным
в условии теоремы о формуле полной
вероятности и .
Тогда справедлива формула Байеса
.
Тогда справедлива формула Байеса
 .
.
Доказательство. Используя определение условной вероятности, получим
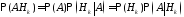 ,
,
откуда
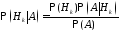 .
.
Далее,
расписав в знаменателе
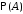 по формуле полной вероятности, получим
формулу Байеса.
по формуле полной вероятности, получим
формулу Байеса.
Вероятности
гипотез
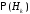 называют еще априорными вероятностями,
а вероятности
называют еще априорными вероятностями,
а вероятности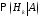 – апостериорными вероятностями (
– апостериорными вероятностями (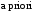 – до опыта,
– до опыта,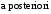 – после опыта).
– после опыта).
Если
гипотезы две –
 и
и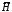 ,
то формулы Байеса для апостериорных
вероятностей имеет вид
,
то формулы Байеса для апостериорных
вероятностей имеет вид
 ,
,
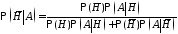 .
.
3.
Для
решения задачи воспользуемся методом
Фурье (разделения переменных). Нетривиальные
решения уравнения
 будем искать в виде
будем искать в виде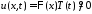 .
Подставляем в уравнение и разделяем
переменные:
.
Подставляем в уравнение и разделяем
переменные:
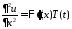 ,
,
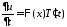 ,
,
 :
:
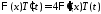 ,
,
 ,
,
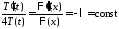 ,
, .
.
Тогда
функции
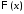 и
и являются соответственно решениями
уравнений
являются соответственно решениями
уравнений
 ,
,
 .
.
Из
граничных условий
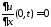 ,
, получаем краевые условия для функции
получаем краевые условия для функции :
: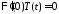 ,
, ,
значит,
,
значит, ,
,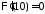 .
Таким образом, для определения
.
Таким образом, для определения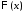 и
и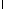 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
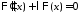
 :
:
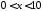 ,
,
 ,
,
 .
.
Поскольку
мы имеем дело со второй краевой задачей,
то
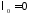 является собственным значением, а
является собственным значением, а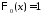 – соответствующей ему собственной
функцией.
– соответствующей ему собственной
функцией.
Пусть
теперь
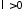 (при
(при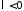 задача имеет только тривиальные решения).
Общее решение уравнения
задача имеет только тривиальные решения).
Общее решение уравнения имеет вид
имеет вид
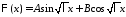 .
.
Тогда
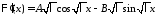 .
Из краевого условия
.
Из краевого условия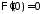 получаем:
получаем: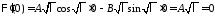 ,
, ,
т.е.
,
т.е.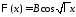 и
и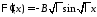 .
.
Из
краевого условия
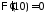 получаем:
получаем: .
Поскольку
.
Поскольку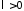 и
и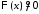 ,
то
,
то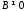 и равенство
и равенство возможно тогда и только тогда, когда
возможно тогда и только тогда, когда ,
откуда получаем
,
откуда получаем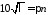 ,
,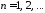 ,
т.е.
,
т.е. ,
, .
Тогда получим
.
Тогда получим ,
, .
Таким образом, получили решение задачи
Штурма-Лиувилля:
.
Таким образом, получили решение задачи
Штурма-Лиувилля:
собственные
значения
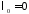 ,
, ,
,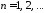 ;
;
собственные
функции
 ,
,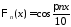 ,
,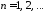 .
.
Теперь
при каждом
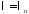 решаем уравнение для
решаем уравнение для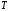 :
:
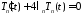 ,
,
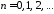 .
.
При
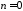 получим уравнение
получим уравнение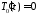 ,
откуда
,
откуда
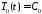 .
.
При
 общее решение этого уравнения имеет
вид
общее решение этого уравнения имеет
вид
 .
.
Тогда
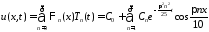 .
.
Для
нахождения коэффициентов
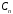 ,
, ,
воспользуемся начальным условием
,
воспользуемся начальным условием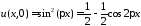 .
.
Из начального условия получаем:
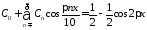 ,
,
откуда
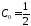 ,
,
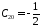 ,
, ,
, ,
, .
.
Тогда решением задачи является функция
 .
.
4.
Вероятность того, что
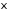 попадет на
попадет на найдем, интегрируя плотность
найдем, интегрируя плотность от
от до
до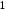 :
:
 .
.
