
- •Экзаменационный билет № 01
- •Экзаменационный билет № 02
- •Экзаменационный билет № 03
- •Экзаменационный билет № 04
- •Экзаменационный билет № 05
- •Экзаменационный билет № 06
- •Экзаменационный билет № 07
- •Экзаменационный билет № 08
- •Экзаменационный билет № 09
- •Экзаменационный билет № 10
- •Экзаменационный билет № 11
- •Экзаменационный билет № 12
- •Экзаменационный билет № 13
- •Экзаменационный билет № 14
- •Экзаменационный билет № 15
- •Экзаменационный билет № 16
- •Экзаменационный билет № 17
- •Экзаменационный билет № 18
- •Экзаменационный билет № 19
- •Экзаменационный билет № 20
Экзаменационный билет № 04
1. Задача Коши для однородного волнового уравнения в трехмерном пространстве. Формула Кирхгофа
2.
Функция распределения случайной
величины, её свойства. Доказать, что
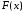 неубывающая.
неубывающая.
3.
Решить задачу Дирихле для уравнения
Лапласа
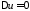 в круге радиуса
в круге радиуса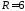 .
ГУ:
.
ГУ: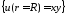 .
.
4.
Баскетболист попадает в корзину с
вероятностью
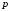 .
Он делает 5 бросков. Найти вероятность
того, что успешными будут только первый
и третий.
.
Он делает 5 бросков. Найти вероятность
того, что успешными будут только первый
и третий.
1. Задача Коши для однородного волнового уравнения в трехмерном пространстве имеет вид
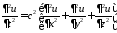 ,
,
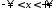 ,
,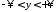 ,
,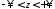 ,
,
начальные
условия:
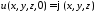 ,
,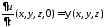 .
.
Функции
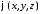 – начальные возмущения,
– начальные возмущения,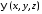 – начальные скорости.
– начальные скорости.
Используя операцию усреднения по сфере к уравнению и начальным условиям, получаем решение задачи Коши для трехмерного волнового уравнения в виде формулы Кирхгофа
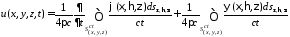 ,
,
где
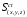 – сфера радиуса
– сфера радиуса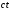 с центром в точке
с центром в точке .
.
2.
Определение. Функцией распределения
случайной величины
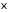 называется определенная на всей числовой
оси функция
называется определенная на всей числовой
оси функция
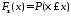 .
.
Основные свойства функции распределения:
1)
для всех
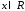
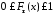 ;
;
2)
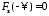 ,
,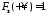 ;
;
3)
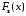 – неубывающая на
– неубывающая на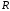 ,
т.е. для любых
,
т.е. для любых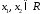 из того, что
из того, что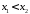 следует, что
следует, что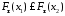 .
.
Докажем
последнее свойство. Пусть
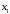 ,
,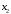 – произвольные действительные числа,
причем
– произвольные действительные числа,
причем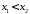 .
Тогда
.
Тогда
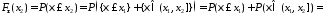
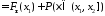 ,
,
откуда
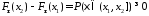 ,
,
то
есть
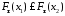 .
.
Кроме того, при доказательстве была получена формула
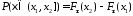 ,
,
которая позволяет проводить расчет вероятностей для случайной величины, если известна её функция распределения.
3.
Задача Дирихле для уравнения Лапласа
в круга радиуса
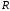 ставится следующим образом:
ставится следующим образом:
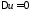 при
при
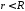 ,
,
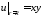 ,
,
где
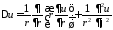 – оператор Лапласа в полярных координатах
– оператор Лапласа в полярных координатах ,
,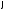 (
(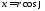 ,
,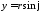 ).
Граничное условие преобразуем в полярные
координаты:
).
Граничное условие преобразуем в полярные
координаты:
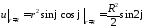 .
.
Из условия однозначности решения вытекает условие периодичности
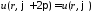 .
.
Для нахождения решения этой задачи используем метод Фурье.
Нетривиальные
решения уравнения
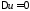 будем искать в виде
будем искать в виде
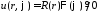 ,
,
Подставляем
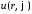 в уравнение и разделяем переменные:
в уравнение и разделяем переменные:
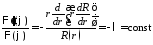 ,
,
откуда
 ,
,
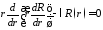 .
.
Из условия периодичности следует, что
 ,
,
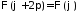 .
.
Таким
образом, для
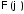 получаем задачу на собственные значения
получаем задачу на собственные значения
 ,
,
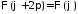 .
.
Если
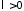 ,
то
,
то
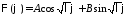 .
.
Применяем условие периодичности:
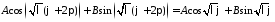 .
.
Отсюда,
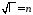 ,
,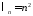 ,
,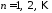 .
.
Если
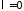 ,
то
,
то
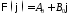 .
.
Следует
взять
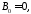 иначе не выполнится условие периодичности.
иначе не выполнится условие периодичности.
При
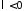 ненулевых периодических решений нет.
ненулевых периодических решений нет.
Окончательно имеем
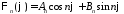 ,
,
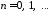 .
.
Чтобы
решить уравнение для
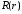 при
при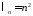 ,
сделаем замену
,
сделаем замену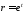 .
Получим
.
Получим
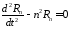 ,
,
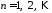 ,
,
откуда
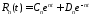 ,
,
т.е.
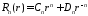 ,
,
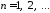 .
.
При
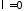 получим
получим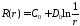 .
.
Таким образом, функции
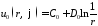 ,
,
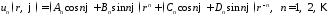
являются
частными решениями уравнения
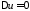 .
Составим функцию
.
Составим функцию
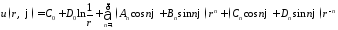 ,
,
которая вследствие линейности и однородности уравнения Лапласа также будет его решением.
Поскольку
задача рассматривается в круге радиуса
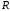 ,
то следует положить равными нулю
коэффициенты при частных решениях,
которые является неограниченными в
области
,
то следует положить равными нулю
коэффициенты при частных решениях,
которые является неограниченными в
области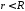 ,
т.е.
,
т.е.
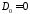 ,
,
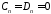 ,
,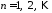 .
.
Итак,
в области
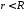 имеем
имеем
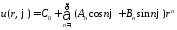 .
.
Для
нахождения
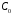 ,
,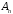 ,
,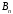 ,
,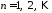 ,
воспользуемся граничным условием
,
воспользуемся граничным условием :
:
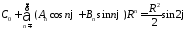 .
.
Тогда
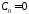 ,
,
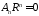 ,
,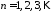
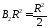 ,
,
 ,
,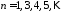 .
.
Тогда
в ряде для
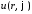 ненулевым являются только коэффициент
ненулевым являются только коэффициент
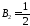 .
.
У
нас
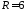 ,
поэтому окончательно решение заданной
задачи Дирихле для уравнения Лапласа
в круге имеет вид
,
поэтому окончательно решение заданной
задачи Дирихле для уравнения Лапласа
в круге имеет вид
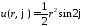 .
.
4.
Баскетболист попадает в корзину с
вероятностью
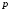 .
Он делает 5 бросков. Найти вероятность
того, что успешными будут только первый
и третий.
.
Он делает 5 бросков. Найти вероятность
того, что успешными будут только первый
и третий.
4.
Введем в рассмотрение события
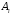 – баскетболист попал в корзину при
– баскетболист попал в корзину при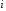 -м
броске,
-м
броске,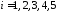 .
По условию
.
По условию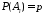 .
Тогда вероятность промаха
.
Тогда вероятность промаха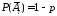 .
Событие
.
Событие
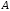 –из
пяти бросков баскетболиста только
первый и третий будут удачными
–из
пяти бросков баскетболиста только
первый и третий будут удачными
можно записать так:
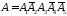 .
.
Считая, что баскетболист при каждом броске попадает или промахивается независимо от остальных бросков по теореме умножения получим
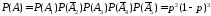 .
.
