Экзаменационный билет № 17

1. Задача Неймана для уравнения Лапласа. Условие разрешимости.

2. Формула полной вероятности (с доказательством). Формула Байеса.

3. Решить смешанную задачу для волнового уравнения

, ,

ГУ: ; НУ:.

4. Случайная величина задана плотностью вероятностиНайтии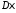.(в билете опечатка: для приведенной в нем плотности не выполняется условие нормировки, я исправил как надо)

1. Задача Неймана для уравнения Лапласа имеет вид:

в области ,

,

где – оператор Лапласа,– граница области,– нормаль к границе.

Задача Неймана имеет решение не для любой функции , а только для такой, для которой выполнено условие

(поверхностный интеграл по границе области равен нулю).

Докажем это условие. Во второй формуле Грина

возьмем – гармоническая вфункция (т.е.), а(тогда,).

Тогда формула Грина примет вид

,

откуда с учетом условия Неймана и получаем условие разрешимости в виде

Если условие разрешимости выполнено, то задача Неймана для уравнения Лапласа имеет бесчисленное множество решений.

2. События образуют полную группу попарно несовместных событий, если:

а) они являются попарно несовместными, т.е. при;

б) .

Теорема. Пусть – некоторое событие, а событияобразуют полную группу попарно несовместных событий. Тогда имеет место формула полной вероятности

.

Доказательство. Заметим, что событие можно представит в виде суммы попарно несовместных событий (рис.):

.

Рис.

Используя теорему сложения, получим

.

Применяя к слагаемым последней суммы теорему умножения

,

получим

.

События называют гипотезами.

Часто бывает, что событие может происходить при двух взаимоисключающих условияхи. Если, то событияиобразуют полную группу событий и формулу полной вероятности можно записать в виде

.

Теорема. Пусть события удовлетворяют условиям, сформулированным в условии теоремы о формуле полной вероятности и. Тогда справедлива формула Байеса

.

Доказательство. Используя определение условной вероятности, получим

,

откуда

.

Далее, расписав в знаменателе 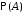по формуле полной вероятности, получим формулу Байеса.

Вероятности гипотез называют еще априорными вероятностями, а вероятности– апостериорными вероятностями (– до опыта,– после опыта).

Если гипотезы две – и, то формулы Байеса для апостериорных вероятностей имеет вид

, .

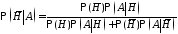3. Сначала найдем общее решение однородного уравнения при нулевых граничных условиях. Для этого воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения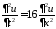будем искать в виде. Подставляем в уравнение и разделяем переменные:

, ,

: ,

, ,.

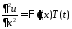Тогда функции и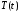являются соответственно решениями уравнений

, .

Из граничных условий ,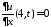получаем краевые условия для функции:,, значит,,. Таким образом, для определенияиполучаем задачу Штурма-Лиувилля

: ,

, .

Поскольку мы имеем дело со второй краевой задачей, то является собственным значением, а– соответствующей ему собственной функцией.

Пусть теперь (призадача имеет только тривиальные решения). Общее решение уравненияимеет вид

.

Тогда . Из краевого условияполучаем:,,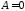 т.е.и.

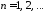Из краевого условия получаем:. Посколькуи, тои равенствовозможно тогда и только тогда, когда, откуда получаем,, т.е.,. Тогда получим,. Таким образом, получили решение задачи Штурма-Лиувилля:

собственные значения ,,;

собственные функции ,,.

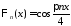Разложим функцию в ряд Фурье на отрезкепо системе собственных функций:

,

где

,

,

так как

,

Находим:

при

,

при

.

Заметим, что

, ,

, .

Тогда

.

Решение смешанной задачи для неоднородного волнового уравнения будем искать в виде ряда

,

где функции ,, подберем так, чтобы удовлетворить неоднородному уравнению и начальным условиям. Заметим, что функцияпри любом выборе функций,, точно удовлетворяет однородным граничным условиям,. Находим производные

, ,

,

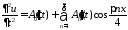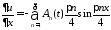и подставляем их в неоднородное уравнение:

,

,

,

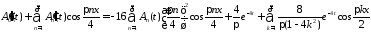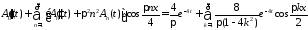откуда получим, что функции ,, удовлетворяют уравнениям

,

, ,

.

Из начальных условий получаем:

,

,

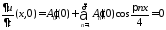откуда

, .

Итак, функции ,,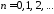 являются решениями задач Коши

, ,;

, ,;

, ,.

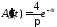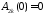Решаем задачу для :

, ,

: ,,

: ,.

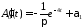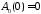Тогда

Задачи для ,, имею в силу единственности только нулевое решение:

, .

Решаем задачи для 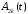. Уравнение– неоднородное линейное уравнение второго порядка с постоянными коэффициентами. Общее решение соответствующего однородного имеет вид

.

Частное решение неоднородного уравнения будем искать в виде

.

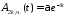Тогда

, ,

,

,

Значит, общее решение уравнения для есть

.

Найдем ,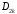из начальных условий:

: ,,

,

: ,

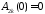Итак,

.

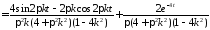Окончательно получим решение смешанной задачи для неоднородного волнового уравнения при нулевых граничных условиях в виде

.

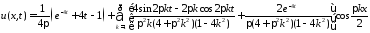4. Математическое ожидание и дисперсию найдем соответственно по формулам:

, .

Для заданной плотности имеем:

,

.