
- •Экзаменационный билет № 01
- •Экзаменационный билет № 02
- •Экзаменационный билет № 03
- •Экзаменационный билет № 04
- •Экзаменационный билет № 05
- •Экзаменационный билет № 06
- •Экзаменационный билет № 07
- •Экзаменационный билет № 08
- •Экзаменационный билет № 09
- •Экзаменационный билет № 10
- •Экзаменационный билет № 11
- •Экзаменационный билет № 12
- •Экзаменационный билет № 13
- •Экзаменационный билет № 14
- •Экзаменационный билет № 15
- •Экзаменационный билет № 16
- •Экзаменационный билет № 17
- •Экзаменационный билет № 18
- •Экзаменационный билет № 19
- •Экзаменационный билет № 20
Экзаменационный билет № 15
1. Задача Дирихле для уравнения Лапласа в кольце.
2.
Закон больших чисел (теорема о связи
 и
и ,
где
,
где ,
,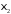 ,
…,
,
…,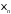 – попарно независимые величины, дисперсии
которых ограничены одной и той жеconst)
(с доказательством).
– попарно независимые величины, дисперсии
которых ограничены одной и той жеconst)
(с доказательством).
3. Решить смешанную задачу для волнового уравнения
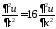 ,
,
 ,
,
ГУ:
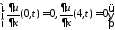 ;
;
НУ:
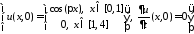 .
.
4. Найти вероятность того, что при семи подбрасываниях двух игральных кубиков пять очков в сумме появятся ровно 3 раза.
1. Уравнением Лапласа называется уравнение вида
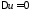 ,
,
где
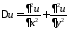 – оператор Лапласа.
– оператор Лапласа.
Задача Дирихле для уравнения Лапласа в кольце ставится следующим образом:
 при
при
 ,
,
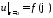 ,
,
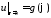 ,
,
где
 – оператор Лапласа в полярных координатах
– оператор Лапласа в полярных координатах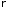 ,
,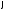 (
( ,
,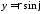 ),
), ,
,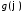 – заданные функция.
– заданные функция.
Из условия однозначности решения вытекает условие периодичности
 .
.
Для нахождения решения этой задачи используем метод Фурье.
Нетривиальные
решения уравнения
 будем искать в виде
будем искать в виде
 ,
,
Подставляем
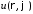 в уравнение и разделяем переменные:
в уравнение и разделяем переменные:
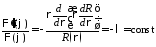 ,
,
откуда
 ,
,
 .
.
Из условия периодичности следует, что
 ,
,
 .
.
Таким
образом, для
 получаем задачу на собственные значения
получаем задачу на собственные значения
 ,
,
 .
.
Если
 ,
то
,
то
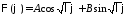 .
.
Применяем условие периодичности:
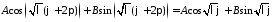 .
.
Отсюда,
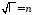 ,
,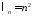 ,
, .
.
Если
 ,
то
,
то
 .
.
Следует
взять
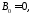 иначе не выполнится условие периодичности.
иначе не выполнится условие периодичности.
При
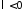 ненулевых периодических решений нет.
ненулевых периодических решений нет.
Окончательно имеем
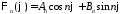 ,
,
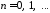 .
.
Чтобы
решить уравнение для
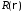 при
при ,
сделаем замену
,
сделаем замену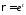 .
Получим
.
Получим
 ,
,
 ,
,
откуда
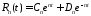 ,
,
т.е.
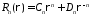 ,
,
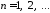 .
.
При
 получим
получим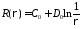 .
.
Таким образом, функции
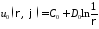 ,
,

являются
частными решениями уравнения
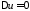 .
Составим функцию
.
Составим функцию
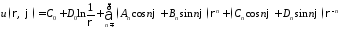 ,
,
которая вследствие линейности и однородности уравнения Лапласа также будет его решением.
Для
нахождения
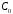 ,
,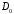 ,
,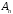 ,
, ,
,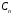 ,
, ,
, ,
воспользуемся краевыми условием
,
воспользуемся краевыми условием ,
,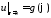 .
Разложим функции
.
Разложим функции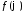 ,
, в тригонометрический ряд Фурье в
промежутке
в тригонометрический ряд Фурье в
промежутке :
:
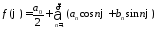 ,
,
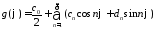 ,
,
где
 ,
,
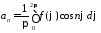 ,
, ,
, ,
,
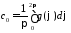 ,
,
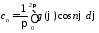 ,
,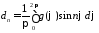 ,
,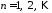 .
.
Тогда
краевое условие
 дает равенство
дает равенство
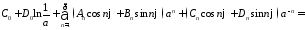
 ,
,
откуда
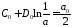 ,
,
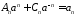 ,
,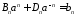 ,
, .
.
Краевое
условие
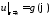 дает равенство
дает равенство
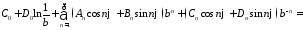
 ,
,
откуда
 ,
,
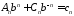 ,
,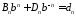 ,
,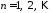 .
.
Тогда
из
системы
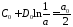 ,
, находим
находим
 ,
,
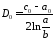 ;
;
из
систем
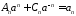 ,
,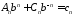 ,
,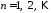 ,
находим
,
находим
 ,
,
 ,
,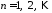 ;
;
из
систем
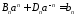 ,
,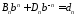 ,
, ,
находим
,
находим
 ,
,
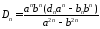 ,
,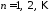 .
.
Окончательно решение задачи Дирихле для уравнения Лапласа в кольце имеет вид


 .
.
2.
Пусть
 – последовательность случайных величин,
для которых определены математические
ожидания
– последовательность случайных величин,
для которых определены математические
ожидания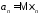 ,
, .
Кроме того, пусть для любого
.
Кроме того, пусть для любого
 .
.
Математические теоремы, формулирующие условия такой сходимости, носят название закона больших чисел (ЗБЧ).
Рассмотрим закон больших чисел в форме Чебышева.
Введем обозначения
 ,
,
 .
.
Теорема
Чебышева. Пусть
 – последовательность независимых
случайных величин, имеющих конечные
математические ожидания
– последовательность независимых
случайных величин, имеющих конечные
математические ожидания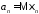 и дисперсии, ограниченные в совокупности:
и дисперсии, ограниченные в совокупности: при любом
при любом .
Тогда для любого
.
Тогда для любого
 .
.
Доказательство.
Поскольку случайные величины
 независимы, то
независимы, то
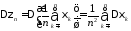 ,
,
Кроме того,
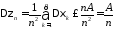 ,
,
поскольку
дисперсии
 ограничены в совокупности.
ограничены в совокупности.
Применим
к вероятности
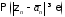 неравенство Чебышева и неравенство для
неравенство Чебышева и неравенство для :
:
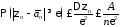 .
.
Последнее
при любом
 стремится к нулю при
стремится к нулю при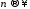 .
Теорема доказана.
.
Теорема доказана.
3.
Для решения задачи воспользуемся методом
Фурье (разделения переменных). Нетривиальные
решения уравнения
 будем искать в виде
будем искать в виде .
Подставляем в уравнение и разделяем
переменные:
.
Подставляем в уравнение и разделяем
переменные:
 ,
,
 ,
,
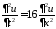 :
:
 ,
,
 ,
,
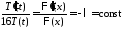 ,
, .
.
Тогда
функции
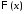 и
и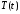 являются соответственно решениями
уравнений
являются соответственно решениями
уравнений
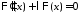 ,
,
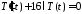 .
.
Из
граничных условий
 ,
, получаем краевые условия для функции
получаем краевые условия для функции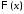 :
: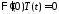 ,
, ,
значит,
,
значит, ,
,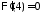 .
Таким образом, для определения
.
Таким образом, для определения и
и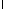 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
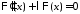
 :
:
 ,
,
 ,
,
 .
.
Поскольку
мы имеем дело со второй краевой задачей,
то
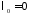 является собственным значением, а
является собственным значением, а – соответствующей ему собственной
функцией.
– соответствующей ему собственной
функцией.
Пусть
теперь
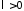 (при
(при задача имеет только тривиальные решения).
Общее решение уравнения
задача имеет только тривиальные решения).
Общее решение уравнения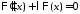 имеет вид
имеет вид
 .
.
Тогда
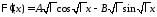 .
Из краевого условия
.
Из краевого условия получаем:
получаем: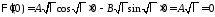 ,
, ,
т.е.
,
т.е.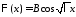 и
и .
.
Из
краевого условия
 получаем:
получаем: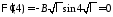 .
Поскольку
.
Поскольку и
и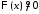 ,
то
,
то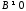 и равенство
и равенство возможно тогда и только тогда, когда
возможно тогда и только тогда, когда ,
откуда получаем
,
откуда получаем ,
,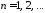 ,
т.е.
,
т.е. ,
, .
Тогда получим
.
Тогда получим ,
,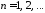 .
Таким образом, получили решение задачи
Штурма-Лиувилля:
.
Таким образом, получили решение задачи
Штурма-Лиувилля:
собственные
значения
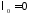 ,
, ,
,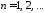 ;
;
собственные
функции
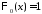 ,
,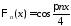 ,
,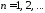 .
.
Теперь
при каждом
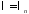 решаем уравнение для
решаем уравнение для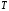 :
:
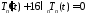 ,
,
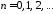 .
.
При
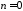 получим уравнение
получим уравнение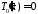 ,
откуда
,
откуда
 .
.
При
 общее решение этого уравнения имеет
вид
общее решение этого уравнения имеет
вид
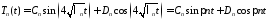 .
.
Тогда
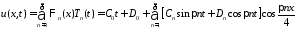 .
.
Для
нахождения коэффициентов
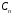 ,
,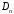 ,
,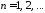 ,
воспользуемся начальными условиями
,
воспользуемся начальными условиями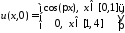 ,
,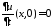 .
.
Разложим
функцию
 на отрезке
на отрезке в ряд Фурье по системе
в ряд Фурье по системе :
:
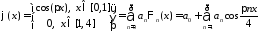 ,
,
где
 ,
,
 .
.
Находим
 ,
,
при

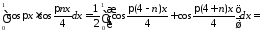

 ,
,
при
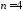
 .
.
Итак,

 .
.
Тогда
начальное условие
 дает
дает
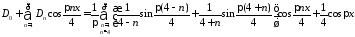 ,
,
откуда
 ,
,
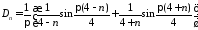 ,
,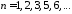 ,
,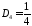 .
.
Находим
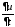 :
:
 .
.
Тогда
начальное условие
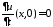 дает
дает
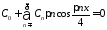 ,
,
откуда
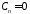 ,
,
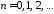 .
.
Тогда решение задачи есть ряд
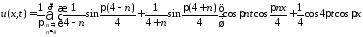 .
.
4.
Мы имеем дело с последовательностью
независимых испытаний по схеме Бернулли,
где событие «успех» – выпадение при
подбрасывании двух игральных кубиков
в сумме пяти очков. Поскольку при
подбрасывании двух игральных кубиков
всего возможно
 исходов, а сумме 5 может появиться
четырьмя способами:
исходов, а сумме 5 может появиться
четырьмя способами: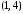 ,
,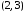 ,
, ,
, ,
то вероятность «успеха» равна
,
то вероятность «успеха» равна .
Проведено
.
Проведено испытаний. Тогда по формуле Бернулли
вероятность того, что «успех» появится
ровно 3 раза (т.е. при семи подбрасываниях
двух игральных кубиков пять очков в
сумме появятся ровно 3 раза), равна
испытаний. Тогда по формуле Бернулли
вероятность того, что «успех» появится
ровно 3 раза (т.е. при семи подбрасываниях
двух игральных кубиков пять очков в
сумме появятся ровно 3 раза), равна
 .
.
