
- •Экзаменационный билет № 01
- •Экзаменационный билет № 02
- •Экзаменационный билет № 03
- •Экзаменационный билет № 04
- •Экзаменационный билет № 05
- •Экзаменационный билет № 06
- •Экзаменационный билет № 07
- •Экзаменационный билет № 08
- •Экзаменационный билет № 09
- •Экзаменационный билет № 10
- •Экзаменационный билет № 11
- •Экзаменационный билет № 12
- •Экзаменационный билет № 13
- •Экзаменационный билет № 14
- •Экзаменационный билет № 15
- •Экзаменационный билет № 16
- •Экзаменационный билет № 17
- •Экзаменационный билет № 18
- •Экзаменационный билет № 19
- •Экзаменационный билет № 20
Экзаменационный билет № 12
1.
Смешанная задача для неоднородного
уравнения теплопроводности на отрезке
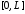 при нулевых граничных условиях
при нулевых граничных условиях .
.
2.
Функция Лапласа
 .
Доказать нечетность этой функции. Связь
между функциями
.
Доказать нечетность этой функции. Связь
между функциями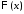 и
и .
.
3. Привести к каноническому виду
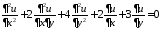 .
.
4. Найти вероятность того, что при шести подбрасываниях двух игральных кубиков четыре очка в сумме появятся ровно 3 раза.
1.
Смешанная задача для неоднородного
уравнения теплопроводности на отрезке
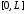 при нулевых граничных условиях имеет
вид:
при нулевых граничных условиях имеет
вид:
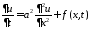 ,
,
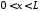 ,
,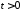 ,
,
граничные
условия:
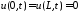 ;
;
начальное
условие:
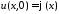 .
.
Сначала
найдем общее решение однородного
уравнения
 при нулевых граничных условиях. Для
этого воспользуемся методом Фурье
(разделения переменных). Нетривиальные
решения уравнения
при нулевых граничных условиях. Для
этого воспользуемся методом Фурье
(разделения переменных). Нетривиальные
решения уравнения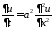 будем искать в виде
будем искать в виде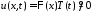 .
Подставляем в уравнение и разделяем
переменные:
.
Подставляем в уравнение и разделяем
переменные:
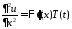 ,
,
 ,
,
 :
:
 ,
,
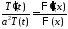 ,
,
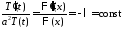 ,
,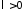 .
.
Тогда
функции
 и
и являются соответственно решениями
уравнений
являются соответственно решениями
уравнений
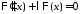 ,
,
 .
.
Из
граничных условий
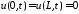 получаем краевые условия для функции
получаем краевые условия для функции :
: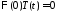 ,
,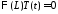 ,
значит,
,
значит, ,
,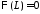 .
Таким образом, для определения
.
Таким образом, для определения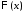 и
и получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля

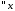 :
:
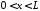 ,
,
 ,
,
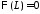 .
.
Поскольку
 (при
(при задача имеет только тривиальные решения),
то общее решение уравнения
задача имеет только тривиальные решения),
то общее решение уравнения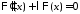 имеет вид
имеет вид
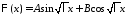 .
.
Из
краевого условия
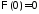 получаем:
получаем: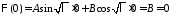 ,
т.е.
,
т.е. .
.
Из
краевого условия
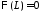 получаем:
получаем: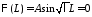 .
Поскольку
.
Поскольку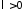 и
и ,
то
,
то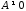 и равенство
и равенство возможно тогда и только тогда, когда
возможно тогда и только тогда, когда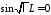 ,
откуда получаем
,
откуда получаем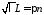 ,
,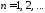 ,
т.е.
,
т.е. ,
, .
Тогда получим
.
Тогда получим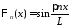 ,
,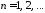 .
Таким образом, получили решение задачи
Штурма-Лиувилля:
.
Таким образом, получили решение задачи
Штурма-Лиувилля:
собственные
значения
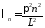 ,
, ;
;
собственные
функции
 ,
,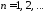 .
.
Разложим
функции
 ,
,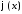 в ряды Фурье на отрезке
в ряды Фурье на отрезке по системе собственных функций
по системе собственных функций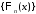 :
:
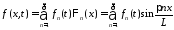 ,
,
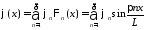 ,
,
где
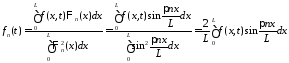
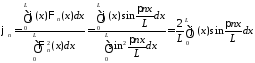 ,
,
так
как
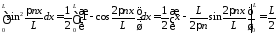 .
.
Решение смешанной задачи для неоднородного уравнения теплопроводности будем искать в виде ряда
 ,
,
где
функции
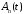 ,
,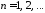 ,
подберем так, чтобы удовлетворить
неоднородному уравнению и начальному
условию. Заметим, что функция
,
подберем так, чтобы удовлетворить
неоднородному уравнению и начальному
условию. Заметим, что функция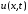 при любом выборе функций
при любом выборе функций ,
,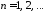 ,
точно удовлетворяет однородным граничным
условиям
,
точно удовлетворяет однородным граничным
условиям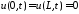 .
Находим производные
.
Находим производные
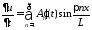 ,
,
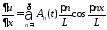 ,
,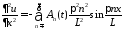
и
подставляем их в неоднородное уравнение
 :
:
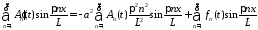 ,
,
 ,
,
откуда
получим, что функции
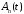 ,
, ,
удовлетворяют уравнениям
,
удовлетворяют уравнениям
 .
.
Из начального условия получаем:
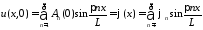 ,
,
откуда
 .
.
Итак,
функции
 ,
,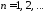 ,
являются решениями задачи Коши
,
являются решениями задачи Коши
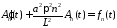 ,
,
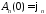 .
.
Найдем
её решение методом вариации. Общее
решение соответствующего однородного
уравнения
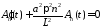 имеет вид
имеет вид
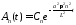 .
.
Решение неоднородного уравнения будем искать в виде
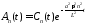 .
.
Находим
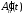 :
:
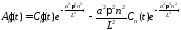 .
.
Подставляем в уравнение:
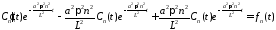 ,
,
 ,
,
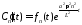 .
.
Из
начального условия
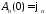 получим
получим
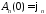
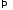
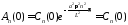
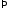
 .
.
Интегрируя
от 0 до
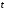 ,
получим
,
получим
 ,
,
 ,
,
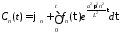 .
.
Тогда
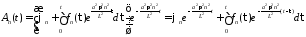 .
.
Окончательно получим решение смешанной задачи для неоднородного уравнения теплопроводности при нулевых граничных условиях в виде
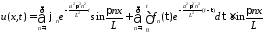 .
.
2.
Пусть случайная величина
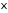 имеет нормальное распределение с
параметрами
имеет нормальное распределение с
параметрами и
и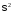 .
При расчете вероятностей, связанных с
нормальными случайными величинами
используют функции
.
При расчете вероятностей, связанных с
нормальными случайными величинами
используют функции и
и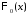 .
Они определяются следующими равенствами:
.
Они определяются следующими равенствами:
 ,
,
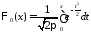 .
.
Функция
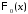 называется функцией Лапласа.
называется функцией Лапласа.
Графики этих функций имеют вид:
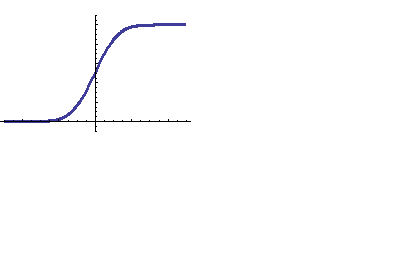


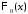
Свойства
функции
 :
:
1)
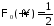 ;
;
2)
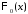 возрастает на всей числовой оси;
возрастает на всей числовой оси;
3)
 – нечетная функция, т.е. для любого
– нечетная функция, т.е. для любого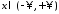
 .
.
Докажем свойство 3):
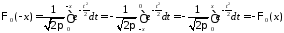 .
.
Функции
 и
и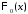 связаны равенством
связаны равенством
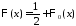 .
.
3.
У нас
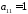 ,
,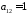 ,
,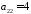 .
Определим тип уравнения. Поскольку
.
Определим тип уравнения. Поскольку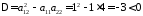 ,
то во всей плоскости уравнение является
эллиптическим. Дифференциальные
уравнения характеристик имеют вид
,
то во всей плоскости уравнение является
эллиптическим. Дифференциальные
уравнения характеристик имеют вид
 ,
,
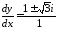 ,
,
решаем его:
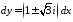 ,
,
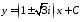 ,
,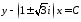 .
.
Для приведения к каноническому виду сделаем в уравнении замену
 ,
,
 .
.
Выражаем частные производные по старым переменным через частные производные по новым переменным:
 ,
,
 ,
,
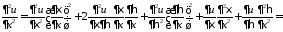
 ,
,
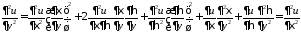 ,
,
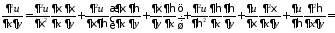
 .
.
Значения производных подставляем в заданное дифференциальное уравнение:
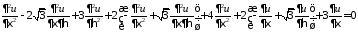 ,
,
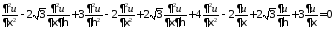 ,
,
 ,
,
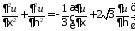 –каноническая
форма эллиптического уравнения.
–каноническая
форма эллиптического уравнения.
4.
Мы имеем дело с последовательностью
независимых испытаний по схеме Бернулли,
где событие «успех» – выпадение при
подбрасывании двух игральных кубиков
в сумме четырёх очков. Поскольку при
подбрасывании двух игральных кубиков
возможно всего
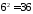 исходов, а сумме 4 может появиться тремя
способами:
исходов, а сумме 4 может появиться тремя
способами: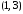 ,
,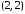 ,
, ,
то вероятность «успеха» равна
,
то вероятность «успеха» равна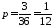 .
Проведено
.
Проведено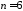 испытаний. Тогда по формуле Бернулли
вероятность того, что «успех» появится
ровно 3 раза (т.е. при шести подбрасываниях
двух игральных кубиков четыре очка в
сумме появятся ровно 3 раза), равна
испытаний. Тогда по формуле Бернулли
вероятность того, что «успех» появится
ровно 3 раза (т.е. при шести подбрасываниях
двух игральных кубиков четыре очка в
сумме появятся ровно 3 раза), равна
 .
.
