
- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Арифметика бесконечно малых последовательностей.
- •Доказательство: (метод деления пополам).
- •Второй замечательный предел:
- •Доказательство:
- •Примеры:
- •Доказательство:
- •Производная сложной функции.
- •2)Доказательство аналогично.
- •Доказательство.
2)Доказательство аналогично.
Достаточное условие строгого экстремума в терминах старшей производной.
Пусть
в точке х0 у функции f(x)
существует n
производных, причём
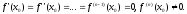 Тогда, если n=2k,
то в точке х0 экстремум, и если
Тогда, если n=2k,
то в точке х0 экстремум, и если
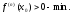
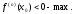 Если n=2k+1
в точке х0 нет экстремума и точка х0 точка
возрастания. Если
Если n=2k+1
в точке х0 нет экстремума и точка х0 точка
возрастания. Если
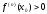
![]() и точка убывания,
и точка убывания,
![]() если
если
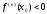 .
.
Следствие.
Если в точке х0 у функции f(x)
существует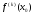 , то, если
, то, если
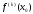 >0,
то в точке х0 минимум,
>0,
то в точке х0 минимум,
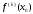 <0,то
в точке х0 максимум (k=1).
<0,то
в точке х0 максимум (k=1).
Доказательство.
Разложим функцию f(x) в ряд Тейлора.
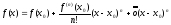 или
или
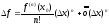 знак
знак
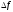 определяется
первым слагаемым, если n
– четное, то знак
определяется
первым слагаемым, если n
– четное, то знак
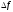 зависит от знака
зависит от знака
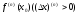 .
По этому, если
.
По этому, если
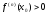 то
то
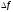 >0
– минимум.
>0
– минимум.
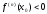 то
то
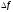 <0
– максимум. Если n
– нечетное, то знак
<0
– максимум. Если n
– нечетное, то знак
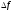 зависит от
зависит от
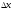 и
и
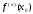 ,
т.е. при переходе через точку х0 знак
,
т.е. при переходе через точку х0 знак
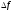 меняется, следовательно в точке х0
экстремума нет.
меняется, следовательно в точке х0
экстремума нет.
Следствие.
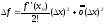 .
f’’(x0)>0,
.
f’’(x0)>0,
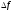 >0
– минимум; f’’(x0)<0,
>0
– минимум; f’’(x0)<0,
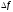 <0
– максимум.
<0
– максимум.
БИЛЕТ 36. Направление выпуклости графика функции. Точки перегиба. Необходимое условие перегиба.
Выпуклости функции. Точка перегиба.
Опр. Функция f(x) на интервале (a,b) называется выпуклой вверх (выпуклой вниз), если
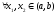
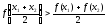 (
(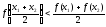 )
)
Геометрически это означает что кривая y=f(x) лежит выше(ниже) прямой.
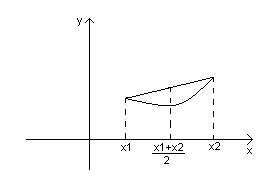
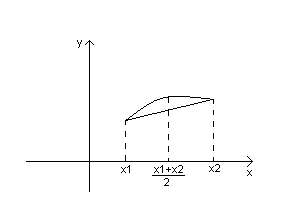
Достаточное условие строго выпуклости.
Теорема. Если на интервале (a,b) f’’(x)>0, то f(x) выпукло вниз, если f’’(x)<0, то f(x) выпукло вверх.
Доказательство
![]()
Рассмотрим
разность
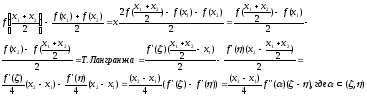 х2-х1>0
х2-х1>0
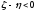
а)Если
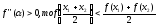 выпукла вниз.
выпукла вниз.
б)
Если
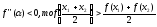 выпукла вверх.
выпукла вверх.
Опр. Точка х0 для функции f(x) называется точкой перегиба, если она является концом интервала выпуклота вверх(вниз) и началом интервала выпуклота вниз(вверх)
![]()
![]()
Необходимое условие точек перегиба.
Если функция дважды непрерывна, дифференцируема в точке х0 и если точка х0 является точкой перегиба, то f’’(x0) = 0
Доказательство. Если бы f’’(x0)>0 то в некоторой окрестности точке х0 f(x) была выпукла вниз. Если бы f’’(x0)<0 то в некоторой окрестности точке х0 f(x) была выпукла вверх. Но это противоречит определению точке перегиба: точка перегиба не принадлежит ни какому интервалу выпуклости.
БИЛЕТ 37. Достаточные условия перегиба графика функции.
Достаточное условие точки перегиба.
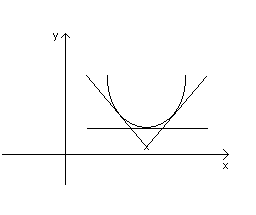
Если функция f(x) дважды дифференцируема в некоторой окрестности точке х0 кроме, быть может, самой точки х0, но f(x) непрерывна в точке х0 и ее производная меняет знак при переходе через точку х0, то в точке х0 – точка перегиба.
Доказательство.
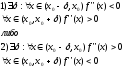
Т.е. в случае (1) точка х0 является концом интервала выпуклости вверх и началом интервала выпуклости вниз, следовательно точка х0 точка перегиба. В случае (2) точка х0 является концом интервала выпуклости вниз и началом интервала выпуклости вверх, следовательно х0 точка перегиба.
Замечание. Заметим, что если функция y=f(x) выпукла вниз, то ее график лежит выше касательной, если функция y=f(x) выпукла вверх, то ее график лежит ниже касательной.
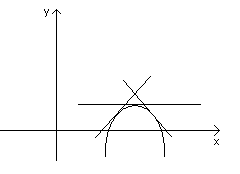
Теорема.
Пусть функция f(x)
обладает следующим условием
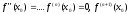 непрерывна в точке x0
и
непрерывна в точке x0
и
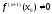 .n-четное
y=
f(x)
выпукла вверх, если
.n-четное
y=
f(x)
выпукла вверх, если
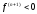 и выпукла вниз, если
и выпукла вниз, если
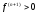 ,
n+1-нечетное-
точка x0-точка
перегиба.
,
n+1-нечетное-
точка x0-точка
перегиба.
