
- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Арифметика бесконечно малых последовательностей.
- •Доказательство: (метод деления пополам).
- •Второй замечательный предел:
- •Доказательство:
- •Примеры:
- •Доказательство:
- •Производная сложной функции.
- •2)Доказательство аналогично.
- •Доказательство.
Доказательство: (метод деления пополам).
I). Проведем построение системы отрезков.
 ограниченная
ограниченная



 .
.
Рассмотрим
точку
 -
середину отрезка
-
середину отрезка
 .
.
1)
В отрезке содержится бесконечное число элементов
содержится бесконечное число элементов
 .
.
Тогда
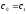 ,
,
 .
.
2)
В противном случае
 ,
,
 ,
,
 -содержит бесконечное число элементов
-содержит бесконечное число элементов
 .
.
Рассмотрим
точку
 -
середину
-
середину
 и
так далее.
и
так далее.
1.

2.
 в
в
 содержится бесконечное число элементов
содержится бесконечное число элементов
 .
.
3.
 .
.
II). Выбор подпоследовательности
По
лемме о вложенных отрезках:

1)
 произвольный
элемент из
произвольный
элемент из

2)
 элемент
из
элемент
из
 :
:

………………………………………………….
k)
 элемент
из
элемент
из
 :
:

Докажем,
что
 .
.






0
(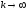 ).
).
 .
.
БИЛЕТ 11. Критерий Коши сходимости последовательности.
Теорема (критерий Коши): Числовая последовательность сходится тогда и только тогда, когда она фундаментальна.
Замечание: Условие необходимости (=>), условие достаточности (<=), критерий- условие необходимости и достаточности (<=>).
1) Необходимость: (=>).
Пусть
 .
Возьмем произвольный
.
Возьмем произвольный
 Тогда
Тогда

 .
.

 .
Обозначим
.
Обозначим ,
тогда
,
тогда

 .
.
 фундаментальна.
фундаментальна.
2) Достаточность: (<=).
1.
 фундаментальна
=>
фундаментальна
=>
 ограниченная
ограниченная



 .
.
Возьмем
 ,
,
 ,
тогда
,
тогда

 .
.
Обозначим
 .
.
 .
.


 ограничена.
ограничена.
2. Теорема Больцано-Вейерштрасса.
 ограниченная
=>
ограниченная
=>
 -
сходящаяся. Обозначим
-
сходящаяся. Обозначим

3.
Докажем, что

Возьмем
произвольный
 .
.
 фундаментальная
=>
фундаментальная
=>


 .
.




Обозначим
 и выберем
и выберем
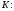
-
k>K
-

Тогда
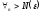 .
.
 .
То есть
.
То есть

БИЛЕТ 12. Два определения предела функции. Эквивалентность определений.
Пусть
 определена
в некоторой выколотой
определена
в некоторой выколотой
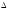 окрестности
т.
окрестности
т.
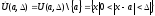
Определение
1 (Гейне):
 ,
если
,
если
 ,
,
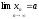 ,
,
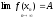
Замечание:

Определение
2 (Коши):
 ,
если
,
если



 .
.
 .
.
Замечание:
 ,
то есть
,
то есть
 .
.
Теорема: Определение 1 <=> Определение 2.
Имеем


 .
.
 .
.
Возьмем
произвольную

 =
= =>
=>
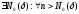
 .
.
Обозначим
 .
Тогда
.
Тогда
 0<
0<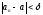 .
.
Т.обр.



 .,
то есть
.,
то есть

БИЛЕТ 13. Свойства пределов функций, связанные с неравенствами.
Теорема:
Пусть
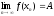 и
и
 ,
тогда
,
тогда
 .
.
Теорема:
(Локальн. Огр.):
Пусть
 ,
тогда
,
тогда
 ,
,
 :
:


 .
.




 .
.
Возьмем
 Тогда
Тогда

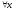
 .
.



Теорема:
Пусть
 ,
,
 и
и



 .
Тогда
.
Тогда

Возьмем
произвольный
 ,
,

 ,
,
 ,
причем
,
причем

 .
.

 (по
теореме о предельном переходе в
неравенство)
(по
теореме о предельном переходе в
неравенство)
 .
.
Теорема:
Пусть
 ,
,
 и
и


 .
Тогда существует
.
Тогда существует
 .
Возьмем произв.
.
Возьмем произв.
 ,
,

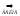
 ,
,
 ,
причем
,
причем



 сущ.
сущ.
 .
.
Теорема
(об отделимости от нуля): Пусть

 ,
,
 :
:


 .
.
Доказательство:




 .
.
Возьмем
 ,
тогда
,
тогда



 ,
,
 ,
,
 .
.
БИЛЕТ 14. Свойства пределов функций, связанные с неравенствами. Теорема об арифметике пределов функций.
Теорема:
(Локальн. Огр.):
Пусть
 ,
тогда
,
тогда
 ,
,
 :
:


 .
.




 .
.
Возьмем
 Тогда
Тогда


 .
.



Теорема:
Если существуют
 и
и
 ,
то:
,
то:
1).



 .
.
2).
 =
= (
( -
постоянная).
-
постоянная).
3).

 *
* .
.
4).



 ,
если
,
если
 .
.
Доказательства:
Доопределив
по непрерывности функции
 и
и в точке
в точке
 ,
положив
,
положив
 =
= и
и
 =
= (это изменение функций не влияет на их
пределы). В точке
(это изменение функций не влияет на их
пределы). В точке
 будут непрерывны функции
будут непрерывны функции
 ,
,
 ,
,
 ,
,
 (так как
(так как
 =
= .
Поэтому в силу равенства
.
Поэтому в силу равенства =
= получим:
получим:
1).

 =
=

 .
.
2).
 =
= =
=
3).

 =
= *
* .
.
4).

 =
=

 .
.
БИЛЕТ 15. Разные виды пределов функции: бесконечно большие функции, пределы функции на бесконечности, односторонний предел. Теорема о связи односторонних пределов с пределом функции.
Определение
1:
Функция ![]() называется бесконечно
большой в точке
называется бесконечно
большой в точке ![]() ,
если для любого
,
если для любого ![]() существует
такое
существует
такое![]() ,
что для любого
,
что для любого ![]() ,
удовлетворяющего неравенству
,
удовлетворяющего неравенству ![]() ,
выполняется неравенство:
,
выполняется неравенство: ![]() .
В этом случае пишут:
.
В этом случае пишут: ![]()
Определение
2:
Число ![]() называется пределом
функции
называется пределом
функции ![]() на
бесконечности или
при
на
бесконечности или
при ![]() ,
если для любого
,
если для любого![]() существует
число
существует
число ![]() такое,
что для всех
такое,
что для всех ![]() из
того, что
из
того, что ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .
.
Определение 3: Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
Число ![]() называется правым
пределом функции
называется правым
пределом функции ![]() в
точке
в
точке ![]() ,
если для
,
если для ![]()
![]() такое,
что для любого
такое,
что для любого ![]() и
и ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() (рис.
1). Правый предел обозначается
(рис.
1). Правый предел обозначается ![]()
Число ![]() называется левым
пределом функции
называется левым
пределом функции ![]() в
точке
в
точке ![]() ,
если для
,
если для ![]()
![]() такое,
что для любого
такое,
что для любого ![]() и
и ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() (рис.
2). Левый предел обозначается
(рис.
2). Левый предел обозначается ![]()
Теорема:
Чтобы функция ![]() имела
предел в точке
имела
предел в точке ![]() ,
необходимо и достаточно чтобы она имела
в этой точке оба односторонних предела
и чтобы они были равны.
,
необходимо и достаточно чтобы она имела
в этой точке оба односторонних предела
и чтобы они были равны.
Функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() ,
если
,
если ![]() .
.
Если
в этом определении раскрыть определение
предела на языке «![]() »,
то получим определение: функция
»,
то получим определение: функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() ,
если
,
если ![]() .
.
Если
же раскрыть определение предела на
языке последовательностей, то приходим
к определению: функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() ,
если для любой последовательности
,
если для любой последовательности ![]() ,
сходящейся к
,
сходящейся к ![]() ,
соответственная последовательность
значений функции
,
соответственная последовательность
значений функции ![]() сходится
к
сходится
к ![]() .
.
Иногда
удобно формулировать определение
непрерывности функции на языке приращений.
Разность ![]()
![]() называют
приращением аргумента в точке
называют
приращением аргумента в точке ![]() ,
а разность
,
а разность ![]() называют
приращением функции
называют
приращением функции ![]() в
точке
в
точке ![]() .
.
Функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() ,
если приращение функции в точке
,
если приращение функции в точке ![]() стремится
к нулю при стремлении к нулю приращения
аргумента, т.е.
стремится
к нулю при стремлении к нулю приращения
аргумента, т.е. ![]() .
.
БИЛЕТ
16.
Первый
замечательный предел (с доказательством).
Второй замечательный предел (без
доказательства).
Первый замечательный предел:

Для
доказательства возьмем вектор
 окружности радиуса 1 с центральным
углом, равным
окружности радиуса 1 с центральным
углом, равным
 (радиан),
(радиан),
 и проведем
и проведем
 .
Тогда пл.
.
Тогда пл.

 <
пл. сект.
<
пл. сект.
 <
пл.
<
пл.

 или
или
 .
Разделив все части этого неравенства
на
.
Разделив все части этого неравенства
на
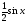 >
0, получим
>
0, получим
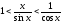 или
или
 .
Это неравенство, доказанное для любых
.
Это неравенство, доказанное для любых
 из интервала (0;
из интервала (0; ),
верно для любого
),
верно для любого
 из
интервала (-
из
интервала (- ;
; )
в силу четности функций, входящих в это
неравенство.
)
в силу четности функций, входящих в это
неравенство.
Докажем,
что

( )
при
)
при

А
раз
 и
и
 ,
то
,
то
 .
.
Кроме
того:
 =
= 1
1
