
- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Арифметика бесконечно малых последовательностей.
- •Доказательство: (метод деления пополам).
- •Второй замечательный предел:
- •Доказательство:
- •Примеры:
- •Доказательство:
- •Производная сложной функции.
- •2)Доказательство аналогично.
- •Доказательство.
Второй замечательный предел:

 .
.
На
первый взгляд кажется, что
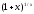 при
при
 имеет пределом единицу (так как 1+
имеет пределом единицу (так как 1+ при
при
 имеет пределом единицу, а единица в
любой степени есть единица). Но в степень
имеет пределом единицу, а единица в
любой степени есть единица). Но в степень
 возводится
1+
возводится
1+ ,
а не единица. И вот из-за этой бесконечно
малой добавки
,
а не единица. И вот из-за этой бесконечно
малой добавки
 предел не равен единице. Чтобы
приблизительно представить себе
поведение функции
предел не равен единице. Чтобы
приблизительно представить себе
поведение функции
 при
малых
при
малых
 приведем таблицу значений этой функции:
приведем таблицу значений этой функции:
|
|
1/2 |
1/3 |
1/4 |
0.01 |
0.001 |
|
|
2.25 |
2.37… |
2.44… |
2.7047… |
2.7169… |
Из
этой таблицы видно, что с уменьшением
 функция увеличивается. Оказывается,
что это имеет место для всех
функция увеличивается. Оказывается,
что это имеет место для всех
 >0,
а из этого следует, что функция имеет
предел.
>0,
а из этого следует, что функция имеет
предел.
БИЛЕТ 17. Бесконечно малые функции. Определение и свойства (без док-ва). Сравнение бесконечно малых функций. Примеры.
Определение:
Функция ![]() называется бесконечно
малой функцией (б.м.ф.) при
называется бесконечно
малой функцией (б.м.ф.) при ![]() (или
в
(или
в
точке ![]() ),
если
),
если
![]() .
.
Основные свойства бесконечно малых функций:
-
Сумма конечного числа б.м функций является функцией б.м.
-
Произведение б.м функции на ограниченную есть функция б.м.
-
Произведение двух б.м функций есть функция б.м.
-
Произведение б.м функции на константу является б.м функцией.
-
Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.
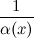
-
Функция , обратная к б.м функции
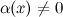 ,
есть функция бесконечно большая.
,
есть функция бесконечно большая.
Верно и обратное.
Бесконечно малые функции одного порядка:
Пусть
и - две б.м. функции
при ![]() .
.![]()
![]()
![]()
Если
, то ![]() является б.м.
более высокого порядка при
является б.м.
более высокого порядка при ![]() ,
чем ,
,
чем , ![]()
![]()
![]()
а
- б.м.
более низкого порядка по сравнению с
:
при ![]() .
.![]()
Пример:
![]() и
и ![]() .
Предел отношений: 2 => одного порядка
.
Предел отношений: 2 => одного порядка
Бесконечно малые функции более низкого и высокого порядков:
Определение 1:
![]()
Если
, то ![]() является б.м.
более высокого порядка при
является б.м.
более высокого порядка при ![]() ,
чем
,
чем ![]() ,
,
а
- б.м.
более низкого порядка по сравнению с ![]() :
: ![]() при
при ![]() .
.![]()
Пример:
![]() и
и
![]() ,
Предел отношений равен 0
,
Предел отношений равен 0
Определение 2:
![]()
Если
, то - б.м.
низшего порядка малости при ![]() по
сравнению с
по
сравнению с ![]()
![]()
Пример:
![]() и
и
![]() ,
Предел отношений равен бесконечности
,
Предел отношений равен бесконечности
Определение 3:
![]()
Если
,
то ![]() называется б.м.
порядка
называется б.м.
порядка ![]() по
сравнению
по
сравнению
с ![]() при
при
![]() .
.
Пример:
![]() и
и
![]() ,
k=2,
предел отношений равен:
1. А 1 не равен 0. Что и требовалось доказать.
,
k=2,
предел отношений равен:
1. А 1 не равен 0. Что и требовалось доказать.
Эквивалентные (равносильные) бесконечно малые функции:
![]()
Если , то б.м.
функции
![]() и
и ![]() называются эквивалентными или равносильными
б.м. одного порядка
при
называются эквивалентными или равносильными
б.м. одного порядка
при ![]() :
: ![]() при
при ![]() .
.
Пример:
![]() и
и ![]() являются
эквивалентными б.м. в точке
являются
эквивалентными б.м. в точке ![]() т.к. предел отношений при x->1
равен 1, также предел a(x)
при x->1
равен 1 и предел b(x)
при x->1
тоже равен 1.
т.к. предел отношений при x->1
равен 1, также предел a(x)
при x->1
равен 1 и предел b(x)
при x->1
тоже равен 1.
БИЛЕТ 18. Эквивалентные бесконечно малые функции. Критерий эквивалентности. Теорема о замене на эквивалентные.
Определение:
функция
 называется
бесконечно
малой
при
называется
бесконечно
малой
при
 ,
если
,
если
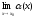 =0.
=0.
Теорема (критерий эквивалентности):
Пусть
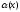 ,
, -бесконечно
малые функции при
-бесконечно
малые функции при
 .
.

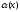 -
- .
Тогда
.
Тогда
 ~
~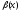 при
при



 .
.
Доказательства:
( ).
Пусть
).
Пусть
 ~
~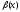 ,
,
 ,
то есть
,
то есть
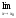
 .
.
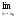


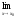
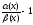 =0,
=0,
то
есть

 .
.
( ).
).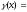
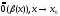 .,
.,
 .
.




 =1.
=1.
Теорема (о замене на эквивалентные):
Пусть
функция
 ~
~ ,
,
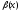 ~
~ при
при
 и существует
и существует

 ,
тогда существует и
,
тогда существует и
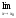
 =
=
 .
То есть выражение или функцию можно
заменять на эквивалентное.
.
То есть выражение или функцию можно
заменять на эквивалентное.

 =
=
 *
* *
* =
=
 .
.


1 1
БИЛЕТ 19. Определения непрерывности функции в точке. Простейшие свойства непрерывных функций.
Определение
1:
Функция
 непрерывна
в точке
непрерывна
в точке
 ,
если
,
если
 .
.
Определение
2:
Функция
 непрерывна
в точке
непрерывна
в точке
 ,
если
,
если
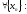
 ,
,
 .
.
Определение
3:
Функция
 непрерывна
в точке
непрерывна
в точке
 ,
если
,
если
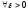
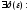


 .
.
Свойства непрерывных функций:
Теорема
1 (локальная огр.): Пусть
функция
 непрерывна
в точке
непрерывна
в точке
 ,
тогда
,
тогда
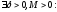

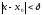
 .
.
Теорема
2 (отделимость от 0): Пусть
функция
 непрерывна
в точке
непрерывна
в точке
 и
и
 ,
тогда
,
тогда


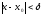
 .
.
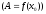 .
.
Теорема
3 (арифметика непрерывных функций):
Пусть
 ,
,
 непрерывны
в точке
непрерывны
в точке
 ,
тогда:
,
тогда:
1).
 непрерывна в точке
непрерывна в точке
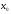 .
.
2).
 непрерывно в точке
непрерывно в точке
 .
.
3).
Если
 ,
то
,
то
 непрерывно
в точке
непрерывно
в точке
 .
.
БИЛЕТ 20. Непрерывность сложной функции.
Теорема:
если функция
 непрерывна
в точке
непрерывна
в точке
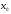 ,
а функция
,
а функция
 непрерывна
в точке
непрерывна
в точке
 то сложная функция
то сложная функция
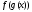 непрерывна в точке
непрерывна в точке
 .
.


