
- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Арифметика бесконечно малых последовательностей.
- •Доказательство: (метод деления пополам).
- •Второй замечательный предел:
- •Доказательство:
- •Примеры:
- •Доказательство:
- •Производная сложной функции.
- •2)Доказательство аналогично.
- •Доказательство.
Доказательство:
Возьмем
число
 >0.
Так как функция
>0.
Так как функция
 непрерывна
в точке
непрерывна
в точке
 то
можно подобрать такое число
то
можно подобрать такое число
 ,
что
,
что
 для
любого
для
любого
 ,
такого, что
,
такого, что
 .
(1)
.
(1)
А
так как функция
 непрерывна в точке
непрерывна в точке
 ,
то для положительного числа
,
то для положительного числа можно подобрать такое число
можно подобрать такое число
 ,
что
,
что
 для
любого
для
любого
 ,
такого, что
,
такого, что
 .
(2)
.
(2)
Возьмем
любое число
 такое, что
такое, что
 .
Тогда в силу (2)
число
.
Тогда в силу (2)
число
 удовлетворяет неравенству
удовлетворяет неравенству
 ,
и поэтому в силу (1)
,
и поэтому в силу (1)
 .
Так как все эти вычисления проведены
для любого
.
Так как все эти вычисления проведены
для любого
 >0,
то непрерывность функции
>0,
то непрерывность функции
 в точке
в точке
 доказана.
доказана.
БИЛЕТ 21. Классификация разрывов. Примеры.
Определение:
 -точка
разрыва функции
-точка
разрыва функции
 ,
если в точке
,
если в точке функция
функция не
является непрерывной.
не
является непрерывной.
Определение:
точка -точка
устранимого разрыва функции
-точка
устранимого разрыва функции
 ,
если существует
,
если существует
 ,
но
,
но
 не
определена в точке
не
определена в точке
 ,
либо
,
либо
 .
.
Замечание: Если в точке устранимого разрыва доопределить (переопределить) функцию:
 -
непрерывна в точке
-
непрерывна в точке
 .
.
Пример:
 .
.
 ,
,
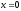 -
точка устранимого разрыва
-
точка устранимого разрыва
 .
.
Если
 не
существует, то
не
существует, то
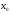 -точка
неустранимого
-точка
неустранимого
разрыва
 .
.
Определение:
Пусть точка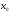 -точка
неустранимого разрыва функции
-точка
неустранимого разрыва функции
 ,
тогда:
,
тогда:
-
если существует
 ,
то
,
то
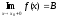 .
. -
если
 ,
то
,
то
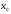 -точка
разрыва функции
-точка
разрыва функции
 1-го рода.
1-го рода. -
если
 ,
то
,
то
 -точка
разрыва функции
-точка
разрыва функции
 2-го рода.
2-го рода.
Примеры:
1).
 .
.
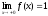 ,
,

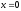 -
точка разрыва
-
точка разрыва
 1-го
рода.
1-го
рода.
2).
 .
.
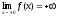 ,
,

 -
точка разрыва
-
точка разрыва
 2-го
рода.
2-го
рода.
3).


 ,
,

 -
точка разрыва
-
точка разрыва
 2-го
рода.
2-го
рода.
4).






 не
существует
не
существует
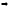 точка
точка
 -
точка разрыва
-
точка разрыва
 2-го
рода.
2-го
рода.
 ,
,
 .
Точка
.
Точка
 -
точка разрыва
-
точка разрыва
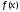 2-го
рода.
2-го
рода.
БИЛЕТ 22. Теорема о нуле непрерывной функции.
Определение:
 непрерывна на
непрерывна на

 ,
если
,
если
 непрерывна в точке
непрерывна в точке
 ,
,

 непрерывна
на
непрерывна
на

 ,
если
,
если
 непрерывна в точке
непрерывна в точке
 ,
,
 и
и
Существует
 ,
,
 .
.
Теорема:
Пусть
 определена на
определена на
 и
и
 ,
причем
,
причем
 .
Тогда
.
Тогда
 .
.

Пусть
 ,
,
 .
Используем метод деления отрезка
пополам.
.
Используем метод деления отрезка
пополам.
Обозначим:
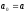 ,
,
 .
.
Определим

1)
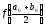 =0
=0 .
.
2)
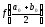 <
0
<
0 ,
,
 .
.
3)
 >
0
>
0 ,
,
 и так далее.
и так далее.

 .
.
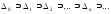

 .
.
По
лемме о вложенных отрезках:
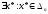
 ,
то есть
,
то есть

 .
.
 непрерывна
в точке
непрерывна
в точке

 .
.



 .
.
0
( )
)

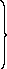
 .
.



 .
.

0
( )
)
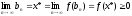
БИЛЕТ 23. Первая теорема Вейерштрасса.
Пусть
 .
Тогда
.
Тогда
 ограничена
на
ограничена
на .
.
Доказательство:
Докажем,
что

 .
.
Предположим
противное, то есть


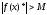 .
Возьмем
.
Возьмем
 =1,2,3…
=1,2,3…
Получим
 :
:
1)



2)

Из
этих определений получаем

 .
.

 =>
=>
 -подпоследовательность
последовательности
-подпоследовательность
последовательности
 :
:
 .
.
 -непрерывна
в точке
-непрерывна
в точке
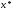 =>
=>
 .
.
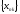 -подпоследовательность
последовательности
-подпоследовательность
последовательности
 :
:
 =>
=>
 .
Противоречие.
.
Противоречие.
Замечание:
Замкнутость
 по
существу.
по
существу.
 ,
,
 ,
но
,
но

Не
является ограниченной на
 .
.
БИЛЕТ 24. Обратная функция. Примеры. Теоремы о существовании и непрерывности обратной функции (без доказательства).
Определение: Пусть на множестве D определена функция у = f(x) и E –множество ее значений. Определим новую функцию, х = h(y), которая определена на множестве Е и каждому значению у ставит в соответствие то самое значение х из множества D, для которого у = f(x). Эта новая функция х = h(y) называется функцией, обратной к функции у = f(x). Таким образом, для нахождения функции, обратной к функции у = f(x), надо решить уравнение у = f(x) относительно х.
Примеры:
![]()
-
Найти функцию обратную для :
-
Область определения функции: D(f) =(-∞;+∞), область значений функции: E(f)=(-∞;+∞)
![]()
-
Выразим x через y - . (По сути это и есть обратная функция, но следует записывать так:)

![]()
-
– это обратная функция функции и наоборот.
![]()
-
Найти функцию обратную для . :
-
Область определения функции: D(f)=ℝ, область значений функции: E(f)=(0;+∞)
![]()
-
Выразим x через y - . (По сути это и есть обратная функция, но следует записывать так:)
![]()
![]()
-
– это обратная функция функции и наоборот.
Теорема: Пусть функция f(x) определена, непрерывна и строго монотонно возрастает (убывает) на отрезке [a,b]. Тогда на отрезке [f(a),f(b)] определена обратная функция f(-1)(x), которая также непрерывна и строго монотонно возрастает (убывает).
БИЛЕТ 26. Производная функции. Дифференцируемость функции. Дифференциал. Геометрический смысл производной.
Производной ![]() от
функции
от
функции ![]() в
точке
в
точке ![]() называется предел отношения
называется предел отношения
![]()
приращения функции ![]() к
приращению аргумента
к
приращению аргумента ![]() :
при
:
при ![]() ,
если он
,
если он
существует, то есть:
![]()
или
![]()
Определение:
Пусть функция f(x) определена в окрестности
точки
 .Если
ее приращение
.Если
ее приращение
 можно представить в виде
можно представить в виде
 ,то
говорят ,что f(x) дифференцируема в точке
,то
говорят ,что f(x) дифференцируема в точке
 (иногда
пишут
(иногда
пишут
 -величина
более высокого порядка, чем
-величина
более высокого порядка, чем
 а это означает, что
а это означает, что
 )
)

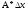 -линейная
функция от
-линейная
функция от
 .Она
называется дифференциалом функции f(x)
и обозначается
.Она
называется дифференциалом функции f(x)
и обозначается
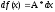
Пример:

Критерий дифференцируемости:
Для
того, чтобы функция y=f(x)
была дифференцируема в точке
 необходимо и достаточно, чтобы существовала
производная в этой точке.
необходимо и достаточно, чтобы существовала
производная в этой точке.
Доказательство:
1.Необходимость.
f(x)
дифференцируема в точке
 это означает
это означает
 .
Разделим это равенство на
.
Разделим это равенство на
 и перейдем к пределу
и перейдем к пределу

 ,т.е. существует
,т.е. существует
 ,
т.е. производная существует.
,
т.е. производная существует.
2.Достаточность.
Пусть существует
 или
или
 ,
т.е. f(x)
дифференцируема в точке
,
т.е. f(x)
дифференцируема в точке
 .
.
Итак,
 ,
т.е.
,
т.е.
 .Отсюда
следует новое обозначение производной
.Отсюда
следует новое обозначение производной
 и эту величину можно рассматривать как
один символ, так и как частное
дифференциалов.
и эту величину можно рассматривать как
один символ, так и как частное
дифференциалов.
Геометрический смысл производной.
Рассмотрим график функции y = f ( x ):

Из рис.1 видно, что для любых двух точек A и B графика функции:

где ![]() - угол
наклона секущей AB.
- угол
наклона секущей AB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей. Если
зафиксировать точку A и двигать
по направлению к ней точку B,
то ![]() неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда
следует: производная функции в точке
есть угловой коэффициент касательной
к графику этой функции в этой точке. В
этом и состоит геометрический
смысл производной.
неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда
следует: производная функции в точке
есть угловой коэффициент касательной
к графику этой функции в этой точке. В
этом и состоит геометрический
смысл производной.
БИЛЕТ 27. Дифференцирование сложной функции.
