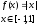- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Арифметика бесконечно малых последовательностей.
- •Доказательство: (метод деления пополам).
- •Второй замечательный предел:
- •Доказательство:
- •Примеры:
- •Доказательство:
- •Производная сложной функции.
- •2)Доказательство аналогично.
- •Доказательство.
Производная сложной функции.
Пусть
функция y=f(x)
имеет производную в точке
 ,а
функция z=F(y)
имеет производную в точке
,а
функция z=F(y)
имеет производную в точке
 ,
тогда сложная функция Ф(x)=F(f(x))
имеет производную в точке
,
тогда сложная функция Ф(x)=F(f(x))
имеет производную в точке

 .
.
Доказательство:
Функция f(x)
непрерывна в окрестности точки
 ,
функция F(y)
непрерывна в окрестности точки
,
функция F(y)
непрерывна в окрестности точки
 ,
поэтому в окрестности точки
,
поэтому в окрестности точки
 существует сложная функция Ф(x).Функция
F(y)
имеет производную в точке
существует сложная функция Ф(x).Функция
F(y)
имеет производную в точке
 ,
поэтому она дифференцируема в этой
точке.
,
поэтому она дифференцируема в этой
точке.
 (\/)
(\/)
 -бесконечно
малая более высокого порядка, чем
-бесконечно
малая более высокого порядка, чем
 ,
но
,
но
 может быть неопределенна в точке
может быть неопределенна в точке
 =0,
поэтому мы доопределяем ее по непрерывности
в точке 0 :
=0,
поэтому мы доопределяем ее по непрерывности
в точке 0 :
 .Разделим
равенство (\/) на
.Разделим
равенство (\/) на
 :
:

F(y)=F(y(x))=Ф(x)
и тогда равенство запишем в виде
 .
Перейдем к пределу
.
Перейдем к пределу

 .
окажем, что
.
окажем, что
 ,
то y=f(x)
непрерывна в окрестности точки
,
то y=f(x)
непрерывна в окрестности точки
 ,
т.е.
,
т.е.
 (
( и
и
 стремятся
к 0 одновременно), т.е.
стремятся
к 0 одновременно), т.е.
 (т.к.
(т.к.
 бесконечно
малая более высокого порядка, чем
бесконечно
малая более высокого порядка, чем
 ),
а
),
а
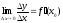 ,
т.о. получим формулу
,
т.о. получим формулу
 .
.
БИЛЕТ 28. Дифференцирование обратной функции.
![]()
![]()
![]()
Теорема: Пусть функция имеет в точке производную . Тогда обратная
![]()
![]()
![]()
функция имеет в соответствующей точке производную , которую можно
отыскать по формуле.
|
|
(4.14) |
Доказательство:
Дадим аргументу приращение
, такое что
, и ![]()
![]()
![]()
![]()
рассмотрим
соответствующее приращение ,
определяемое ![]()
![]()
равенством
. Тогда,
очевидно, ; при ![]()
![]()
![]()
этом , а из монотонности функции следует, что . Поскольку
![]()
![]()
![]()
![]()
как функция , так и функция непрерывны, то условия и эквивалентны.
![]()
Составим теперь разностное отношение для функции и запишем для него очевидное равенство:

![]()
Теперь
перейдём в этом равенстве к пределу при
и учтём, что при этом ![]() тоже
стремится к 0:
тоже
стремится к 0:

что мы и хотели доказать.
Заметим, что, очевидно, из формулы (4.14) следует, что
|
|
(4.15) |
если
-- функция, обратная к
.![]()
![]()
БИЛЕТ 29. Производные высших порядков.
Рассмотрим
дифференцируемую функцию ![]() .
Найдем её производную
.
Найдем её производную ![]() .
Рассматривая
.
Рассматривая ![]() как
новую функцию, продифференцируем её:
как
новую функцию, продифференцируем её:
![]()
Полученную
новую производную называют второй
производной от функции ![]() .
Вторую производную обозначают так:
.
Вторую производную обозначают так:
![]() или
или ![]() .
.
Аналогично находится производная третьего, четвертого, и т.д. n-го порядка. Третья производная обозначается так:
![]()
Четвертая:
![]() .
.
Производной n –
го порядка от функции ![]() называется
производная от производной
называется
производная от производной ![]() -го
порядка:
-го
порядка:
![]() .
.
Производные высших порядков вычисляются последовательным дифференцированием данной функции.
БИЛЕТ 30. Теорема Ферма.
Теорема Ферма (необходимое условие extr):
Пусть
 определена на интервале (a,b)
и точка
определена на интервале (a,b)
и точка
 если
в точке
если
в точке
 функция f(x)
достигает max
или min
значения и в точке
функция f(x)
достигает max
или min
значения и в точке
 существует производная, то f’(
существует производная, то f’( )=0.
)=0.
Доказательство.
Пусть
для определенности в точке

 принимает max
значение, т.е
принимает max
значение, т.е
 .
В точке
.
В точке
 существует производная
существует производная
 ,
тогда
,
тогда
 (правая
и левая производная).Распишем отношение
(правая
и левая производная).Распишем отношение

 переходя
в этих интервалах к пределу, получим
переходя
в этих интервалах к пределу, получим

Замечание.
Теорема
носит локальный характер, т.е. точка
 является локальным экстремумом.
является локальным экстремумом.
Геометрический смысл теоремы.
В предположение теоремы всегда существует точка, в которой касательная к графику функции параллельная OX.


БИЛЕТ 31. Теорема Ролля.
Теорема Ролля:
Пусть
функция y= :
:
1) непрерывна на отрезке [a,b];
2) дифференцируема (a,b);
3)
f(a)=f(b),
тогда

Доказательство.
Функция
f(x),
непрерывна на [a,b]
достигает на нем max
M
и min
m
значения, т.е
 .
Возможны два случая.
.
Возможны два случая.
1)
 и
и

2)
 ,тогда
либо максимальное значение f(x)
либо минимальное значения f(x)
достигается внутри интервала (a,b)
(не на конце отрезка [a,b]).(f(a)=f(b)).
,тогда
либо максимальное значение f(x)
либо минимальное значения f(x)
достигается внутри интервала (a,b)
(не на конце отрезка [a,b]).(f(a)=f(b)).
 ,
тогда
,
тогда
 достигает максимального или минимального
значения во внутренней точке интервала
(a,b)
и по теореме Ферма
достигает максимального или минимального
значения во внутренней точке интервала
(a,b)
и по теореме Ферма

|
|
|
|
|
|
|
|
Все
условия теоремы Ролля существенные.
Если выполняется, только 2 из 3(см.
картинку), то не существует точка причем
 (касательная
параллельная оси ОХ).
(касательная
параллельная оси ОХ).
БИЛЕТ 32. Теорема Лагранжа (формула конечных приращений).
Теорема Лагранжа.
Пусть функция f(x)
-непрерывна на отрезке [a,b];
-дифференцируема на интервале (a,b);
Тогда
 (формула
конечных приращений)
(формула
конечных приращений)
Доказательство.
Рассмотрим
функцию
 .Параметр
.Параметр
 выберем из условия F(a)=F(b)
выберем из условия F(a)=F(b)


Функция
F(x)
удовлетворяет всем условием т.Ролля
(она непрерывна и дифференцируема, как
сумма непрерывных и дифференцируемых
функций )



Геометрический смысл.
В
предположение теоремы существует точка :касательная к графику функции параллельна
секущей(хорде).
:касательная к графику функции параллельна
секущей(хорде).

Следствие.
Пусть
f(x)
определена, непрерывна и дифференцируема
на (a,b).
И в каждой точке интервала (a,b)
 ,
тогда f(x)=const.
,
тогда f(x)=const.
Доказательство.
Пусть
x1
и x2
две произвольные точки интервала(a,b),тогда
 ,
точка
,
точка
 лежит между этими точками x1
и x2,
по условию
лежит между этими точками x1
и x2,
по условию
 ,
т.е f(x)=const(в
силу произвольности выбора x1
и x2).
,
т.е f(x)=const(в
силу произвольности выбора x1
и x2).
БИЛЕТ 33. Теорема Коши (обобщенная формула конечных приращений).
Теорема Коши.
Пусть
функции
 и g(x)
определены на интервале (a,b)
и g(x)
определены на интервале (a,b)
1)
 и g(x)
непрерывны на [a,b];
и g(x)
непрерывны на [a,b];
2)
 и g(x)
дифференцируемы на (a,b)
причем
и g(x)
дифференцируемы на (a,b)
причем
 ,
тогда
,
тогда
Доказательство.
Рассмотрим
функцию
 параметр
параметр
 выбрали из условия
выбрали из условия


 .
.
Для
функции F(x)
выполнены условия теоремы Ролля.
Формулировка теоремы Ролля
 Сравнивания формулы для
Сравнивания формулы для
 ,
получим утверждение теоремы.
,
получим утверждение теоремы.
Следствие.
Теорема
Лагранжа.
Если
 ,то
,то
 .
.
БИЛЕТ 34. Условие постоянства функции. Условие монотонности функции.

На
рисунке нарисован график
 функции
функции
 ,
всюду имеющей производную. В точке
,
всюду имеющей производную. В точке
 касательная к
касательная к
 и ось
и ось
 образуют
острый угол
образуют
острый угол
 ,
поэтому ее угловой коэффициент, равный
,
поэтому ее угловой коэффициент, равный
 ,
положителен. Но
,
положителен. Но
 .
Следовательно,
.
Следовательно,
 .
И так будет в любой точке интервала
.
И так будет в любой точке интервала
 ,
где функция
,
где функция
 монотонно возрастает. Напрашивается
вывод: если на интервале
монотонно возрастает. Напрашивается
вывод: если на интервале
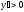 ,
то на этом интервале функция монотонно
возрастает. Далее, в точке
,
то на этом интервале функция монотонно
возрастает. Далее, в точке
 касательная к
касательная к
 образует с осью
образует с осью
 тупой
угол
тупой
угол
 ,
поэтому ее угловой коэффициент, равный
,
поэтому ее угловой коэффициент, равный
 отрицателен. А так как
отрицателен. А так как
 ,
то
,
то
 .
Вывод: если на интервале
.
Вывод: если на интервале
 ,
то на этом интервале функция монотонно
убывает. В точке
,
то на этом интервале функция монотонно
убывает. В точке
 функция имеет максимум. На чертеже ясно,
что в этой точке касательная к
функция имеет максимум. На чертеже ясно,
что в этой точке касательная к
 параллельна оси
параллельна оси
 ,
и поэтому ее угловой коэффициент равен
нулю, так что
,
и поэтому ее угловой коэффициент равен
нулю, так что
 .
При этом слева от этой точки
.
При этом слева от этой точки ,
а справа
,
а справа
 .
.
Теорема (достаточный признак монотонности).
1).
Если
 на
отрезке
на
отрезке
 ,
то
,
то
 монотонно
возрастает на
монотонно
возрастает на
 .
.
2).
Если
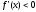 на
отрезке
на
отрезке
 ,
то
,
то
 монотонно
убывает на
монотонно
убывает на
 .
.
Доказательство:
Возьмем
любые числа
 и
и
 ,
причем
,
причем
 <
< ,
из интервала
,
из интервала
 .
По формуле Лагранжа получаем:
.
По формуле Лагранжа получаем:
 ,
,
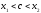 ,
и поэтому
,
и поэтому
 принадлежит интервалу
принадлежит интервалу
 .
Так как
.
Так как
 ,
то в первом случае
,
то в первом случае
 ,
то есть
,
то есть
 ,
а во втором
,
а во втором
 ,
то есть
,
то есть
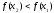 ,
что и требовалось доказать.
,
что и требовалось доказать.
БИЛЕТ 35. Экстремумы функции. Достаточные условия экстремума.
Теорема 1. Необходимое условие экстремума.
Пусть точка х0 является точка экстремума для функции f(x). Тогда, если существует f’(x0), то f’(x0)=0, либо f’(x0) не существует.

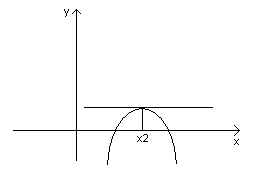


В точке х1 – min; в точке х2 – max.
Теорема 2. Достаточное условие строгого extr в терминах первой производной.
Пусть
f(x)
дифференцируема в некой окрестности
точки х0, и в точке х0 f(x)
непрерывна. Если f’(x)
при переходе через точку х0 меняет знак,
то точка х0 является точкой строгого
экстремума, при этом 1)если при
 ,
а при
,
а при

то
в точке х0 – минимум. 2)если при
 ,
а при
,
а при
 то в точке х0 максимум.
то в точке х0 максимум.
Доказательство.
Докажем
1)
 .Теорема
Лагранжа
.Теорема
Лагранжа
 .
а) Если х-х0>0 и
.
а) Если х-х0>0 и
 .
б) если х-х0<0 и
.
б) если х-х0<0 и
 ,
т.е при переходе через точку х0
,
т.е при переходе через точку х0
 не меняет свой знак:
не меняет свой знак:
 >0,
т.е точка х0-точка минимума.
>0,
т.е точка х0-точка минимума.