
- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Арифметика бесконечно малых последовательностей.
- •Доказательство: (метод деления пополам).
- •Второй замечательный предел:
- •Доказательство:
- •Примеры:
- •Доказательство:
- •Производная сложной функции.
- •2)Доказательство аналогично.
- •Доказательство.
БИЛЕТ 1. Точные грани числовых множеств. Теорема существования (без доказательства)
Точной
верхней гранью
числового множества
 (
( )
называется число
)
называется число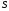 ,
такое что:
,
такое что:
1)
S-
верхняя граница
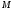 (
(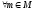
 ).
).
2)
Для любого положительного числа
 в множестве M
можно найти число
в множестве M
можно найти число
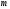 ,
такое что
,
такое что
 >
>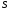 -
- .
(
.
(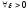

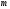 >
>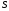 -
- )
)
Точной
нижней гранью
числового множества
 (
( )
называется число
)
называется число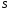 ,
такое что:
,
такое что:
1)
S-
нижняя граница
 (
(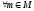
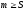 ).
).
2) Для любого положительного числа в множестве m можно найти число , такое что
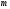

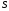 +
+ .
(
.
(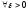
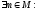
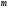

 +
+ )
)
Теорема
существования: Пусть
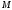

 ,
,

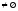 ,
ограниченное сверху (снизу), тогда
существует точная верхняя (нижняя)
грань.
,
ограниченное сверху (снизу), тогда
существует точная верхняя (нижняя)
грань.
БИЛЕТ 2. Бесконечно малые и ограниченные последовательности. Арифметика бесконечно малых последовательностей.
Определение:
Последовательность
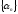 будем называть бесконечно
малой
последовательностью, если
будем называть бесконечно
малой
последовательностью, если
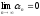 ,
то есть
,
то есть


 .
.
Теорема:
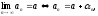
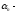 бесконечно
бесконечно
малая последовательность.
(I)-


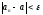
(II)-
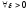


(I) (II)
(II)

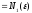
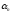 =
=
(II)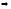 (I)
(I)
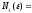
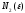
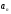 =
=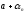
Замечание: Фактически мы дали эквивалентность определений сходящейся последовательности.
Определение:
Последовательность
 будем
называть ограниченной
последовательностью, если
будем
называть ограниченной
последовательностью, если

 .
.
Замечание: Ранее мы доказали, что всякая сходящаяся, в том числе и бесконечно малая последовательность ограничена.
Арифметика бесконечно малых последовательностей.
Теорема: сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Пусть

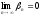 .
Возьмем произвольный
.
Возьмем произвольный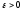 .
.
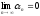


Аналогично

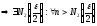
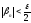 .
.
Обозначим
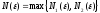 .
.
Тогда
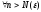
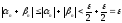 .
.
То
есть
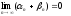
Теорема: произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
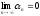 ,
,
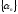 -
ограниченная,
то есть
-
ограниченная,
то есть

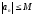 .
.
Возьмем
произвольный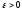 .
.
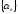 -
бесконечно
малая.
-
бесконечно
малая.


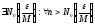
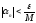 .
.
Обозначим
 .
Тогда
.
Тогда
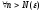
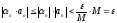 .
.
То
есть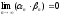
Замечание: сходимость ограниченной последовательности здесь не требуется.
БИЛЕТ 3. Бесконечно большие последовательности. Теорема о связи между бесконечно больших и бесконечно малых последовательностей.
Определение:
Последовательность ![]() называется бесконечно
большой,
если для любого
называется бесконечно
большой,
если для любого ![]() существует номер
существует номер ![]() такой,
что для любого
такой,
что для любого ![]() выполняется неравенство:
выполняется неравенство: ![]()
![]()
Формально:
![]()
Теорема:
Если
![]() - б.б. и все её члены отличны от нуля то
последовательность
- б.б. и все её члены отличны от нуля то
последовательность
бесконечно
малая, и, обратно, если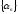 -
б.м. последовательность и все её члены
отличны от
-
б.м. последовательность и все её члены
отличны от
![]()
нуля, то - б.б.
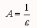
Док-во:
Пусть
![]() - б.б. Возьмем произвольное
- б.б. Возьмем произвольное
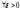 и положим .
и положим .
Согласно
определению для этого существует такой
номер N,
что при
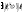 будет
будет
![]() .
Отсюда получаем, что:
.
Отсюда получаем, что: 
![]()
для
всех
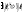 .
А это значит, что последовательность
- б.м.
.
А это значит, что последовательность
- б.м.
БИЛЕТ 4. Предел числовой последовательности. Теорема об арифметике пределов последовательностей (док-во для суммы и произведения).
Определение:
функцию
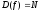 называют
числовой последовательностью.
называют
числовой последовательностью.
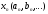 -
члены числовой последовательности.
-
члены числовой последовательности.
 -
номер члена числовой последовательности.
-
номер члена числовой последовательности.
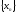 или
или
 ,
,

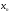 =
= ,
,
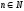 -общий
член.
-общий
член.
Определение:
Число
 называется пределом последовательности
называется пределом последовательности
 (пишут
(пишут
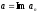 ),
если для любого положительного числа
),
если для любого положительного числа
 (
( >0)
можно указать такое число
>0)
можно указать такое число
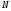 ,
зависящее от
,
зависящее от
 ,
что
,
что
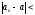
 для всех
для всех
 .
.
Арифметика:
Пусть
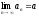 ,
,
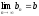 .
Тогда:
.
Тогда:
1)
существует

2)
существует
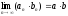
3)
если
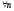
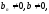 то
существует
то
существует
 .
.
Доказательства:
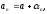
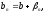 где
где
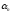 и
и
 -
бесконечно малые последовательности.
-
бесконечно малые последовательности.
1)
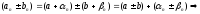

бесконечно малые.
 бесконечно
малые.
бесконечно
малые.


 2)
2)
 =
=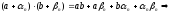
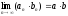
бесконечно малая бесконечно малая
бесконечно малая
Дополнительно:
3)
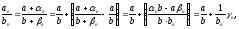 где
где
 -
бесконечно малая последовательность.
-
бесконечно малая последовательность.
По
условию
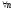

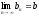
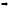

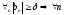
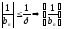 -ограниченная.
-ограниченная.
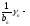 бесконечно
малая.
бесконечно
малая.
БИЛЕТ 5. Единственность предела. Ограниченность сходящейся последовательности.
Теорема:
(о единственности предела): Если
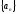 -сходящаяся,
то предел единственный.
-сходящаяся,
то предел единственный.
Доказательство:
Пусть
 ,
,
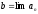 ,
,
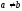 .
.
Для
определенности
 имеем:
имеем:

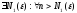








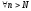 .
.

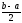
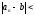

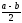 <
<
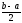
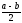 <
<
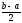
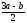 <
<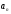

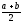 .
.
 <
<

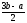 .
.

Противоречие.
Теорема:
(об ограниченности сходящейся
последовательности): Если
 -сходится,
то она ограничена.
-сходится,
то она ограничена.
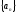 -
сходящаяся
-
сходящаяся


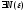 :
:

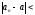
 .
.
Возьмем
 =1
=1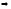
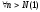
 .
.
Обозначим
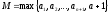 ,
тогда
,
тогда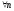
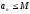
 ,
тогда
,
тогда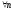

Отсюда
для обоих случаев
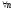


Замечание: обратное не верно.
БИЛЕТ 6. Свойства сходящихся последовательностей, связанные с неравенствами.
Теорема: (о предельном переходе в неравенство):
Пусть
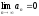 ,
,
 .
.

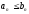 .
Тогда
.
Тогда
 .
.
Доказательство (от противного):
Пусть
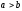 .
.
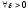
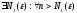
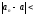

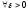
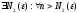
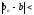

Возьмем
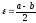 .
.
Обозначим
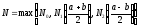
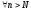 .
.
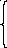

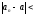
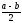


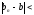
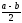
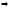


 -
противоречие.
-
противоречие.
Замечание:
Если для элементов последовательности
выполняется
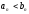 ,
то отсюда не следует, что
,
то отсюда не следует, что
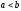 .
.
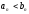
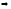
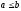 .
.
 =
=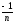 ,
,
 =
= ,
,
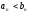
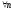

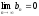 .
.
Теорема (о промежуточной последовательности).
Пусть

 ,
,
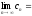
 и
и
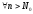
 .
Тогда существует
.
Тогда существует
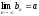 .
.
Доказательство:
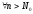
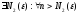


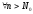



Возьмем
произвольный
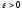 .
.
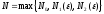 .
Тогда
.
Тогда
 .
.
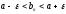 .
(
.
(
 ).
).
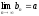 .
.
Теорема: (об отделимости от нуля).
Пусть

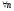 и
и
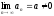 .
Тогда
.
Тогда
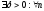
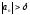 .
.
Замечание:
 -
ограниченная.
-
ограниченная.
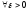
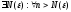
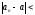
 (
( ).
).
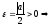
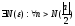
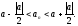

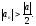
 .
.

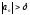 .
.
БИЛЕТ 7. Монотонные последовательности. Теорема о пределе монотонной последовательности.
Определение:
 -монотонно
возрастающая (монотонно убывающая),
если
-монотонно
возрастающая (монотонно убывающая),
если
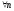
 (
(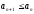 ).
Если неравенства строгие, то
последовательности строго возрастающие
(убывающие).
).
Если неравенства строгие, то
последовательности строго возрастающие
(убывающие).
Теорема
(о пределе монотонной последовательности).
Пусть
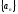 -монотонно
возрастает и ограничена сверху. Тогда
она сходится, причем
-монотонно
возрастает и ограничена сверху. Тогда
она сходится, причем
 .
.
Доказательство:
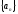 ограничена
сверху =>по теореме существования
точной верхней грани
ограничена
сверху =>по теореме существования
точной верхней грани
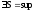
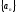 .
Докажем, что
.
Докажем, что
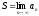 .
.
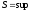
 :
1)
:
1)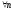
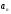
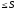
2)
 .
.
Возьмем
произвольный
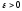 ,
обозначим
,
обозначим
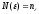 из
2).
из
2).
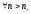 1)=>
1)=>
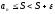
2)=>
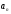
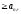 (монот.
возр).
(монот.
возр).
Из
этого следует, что
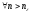 ,
,
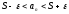 =>
=>

 .
.
Мы доказали достаточное условие числовой сходимости последовательности (монот. и огр.)
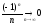 (огр.
на б.м.).
(огр.
на б.м.).
БИЛЕТ 8 Подпоследовательности. Частичные пределы. Теорема о частичных пределах сходящейся подпоследовательности.
Определение:
Пусть дана некая последовательность
 .
Из элементов этой последовательности
извлечем другую последовательность
.
Из элементов этой последовательности
извлечем другую последовательность
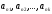 ,
где последовательность
,
где последовательность
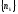 -номера
элементов исходной последовательности,
причем
-номера
элементов исходной последовательности,
причем
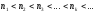 Тогда последовательность
Тогда последовательность
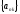 -подпоследовательность
последовательности
-подпоследовательность
последовательности
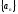 .
.
Замечание:
Элементы подпоследовательности
выбираются в порядке их следования в
исходной последовательности.
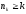 .
.
Определение:
Если
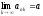 ,
то
,
то
 -частичный
предел
последовательности
-частичный
предел
последовательности
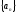 .
.
Теорема
(о частичных пределах сходящейся
подпоследовательности): Пусть
 ,
тогда
,
тогда
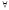
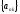
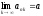 .
.
Доказательство:
Возьмем
произвольный
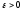 ,
тогда
,
тогда
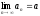
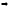
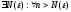
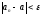 .
.
Возьмем
произвольную
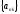 .
Обозначим
.
Обозначим
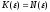 .
Тогда
.
Тогда
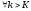 имеем:
имеем:
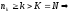
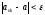 .
Таким образом:
.
Таким образом:
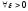

 .
.
Замечание: Понятие частичных пределов для сходящихся последовательностей не нужно.
БИЛЕТ 9. Лемма о вложенных отрезках.
Пусть
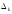 =
= ,
,
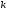 =1,2,…,
причем
=1,2,…,
причем
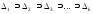 …,
то есть
…,
то есть

 ,
,

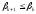 .
Тогда
.
Тогда

 ,
то есть
,
то есть

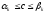 .
.
Доказательство.
Рассмотрим
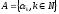 ,
,
 ,
,
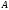 ограничено
сверху, так как любое
ограничено
сверху, так как любое
 является верхней границей множества
является верхней границей множества
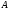 в силу вложенности отрезков.
в силу вложенности отрезков.
 .
Тогда:
.
Тогда:
а)
 -
верхняя граница
-
верхняя граница
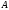 ,
то есть
,
то есть

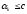 .
.
б)
 -
наименьшая из всех границ, то есть
-
наименьшая из всех границ, то есть
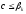 .
.
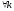
 .
.
Замечание: Если в условиях леммы хотя бы один из концов исключить, то аналогичная лемма будет не верна.

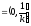 .
.
 (
] ] ] ]
(
] ] ] ]
0 1/3 1/2 1
БИЛЕТ 10. Теорема Больцано-Вейерштрасса.
Теорема: Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
