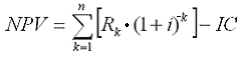Самостоятельное задание №4
Составьте график погашеия кредита по данным из задания 3.1, при условии, что основная сумма долга погашается равнными частями в течение 10 лет. Сравните суммы уплаченных процентов.
12.4. Оценка инвестиционных проектов
Инвестиции – это долгосрочные финансовые вложения экономических ресурсов с целью создания и получения выгоды в будущем, которая должна быть выше начальной величины вложений.
Инвестиционный процесс – это последовательность связанных инвестиций, растянутых во времени, отдача от которых также распределена во времени. Этот процесс характеризуется двусторонним потоком платежей, где отрицательные члены потока являются вложениями денежных средств в инвестиционный проект, а положительные члены потока – доходы от инвестированных средств.
Реализация инвестиционных проектов требует отказа от денежных средств сегодня в пользу получения дохода в будущем, поэтому любой инвестиционный проект требует анализа и оценки.
При анализе потоков платежей используются обобщающие показатели:
наращенная стоимость;
приведенная стоимость;
норма доходности.
Эти показатели уже рассматривались ранее, но для инвестиционных процессов они приобретают свою специфику.
Чистый приведенный доход
Поскольку денежные средства распределены во времени, то и здесь фактор времени играет важную роль.
При оценке инвестиционных проектов используется метод расчета чистого приведенного дохода, который предусматривает дисконтирование денежных потоков: все доходы и затраты приводятся к одному моменту времени.
Центральным показателем в рассматриваемом методе является показатель NPV (net present value) – текущая стоимость денежных потоков за вычетом текущей стоимости денежных оттоков. Это обобщенный конечный результат инвестиционной деятельности в абсолютном измерении.
При разовой инвестиции расчет чистого приведенного дохода можно представить следующим выражением:
|
|
(18) |
где Rk – годовые денежные поступления в течение n лет, k = 1, 2, …, n;
IC – стартовые инвестиции;
i – ставка дисконтирования.
Важным моментом является выбор ставки дисконтирования, которая должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке. Для определения эффективности инвестиционного проекта отдельной фирмой в качестве ставки дисконтирования используется средневзвешенная цена капитала, используемого фирмой для финансирования данного инвестиционного проекта.
Показатель NPV является абсолютным приростом, поскольку оценивает, на сколько приведенный доход перекрывает приведенные затраты:
при NPV > 0 проект следует принять;
при NPV < 0 проект не принимается,
при NPV = 0 проект не имеет ни прибыли, ни убытков.
Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала фирмы в случае принятия данного проекта.
Пример. Фирма рассматривает целесообразность инвестиционного проекта, стоимость которого составляет 210 тыс. долларов. По прогнозам ежегодные поступления составят 55 тыс. долларов. Проект рассчитан на 5 лет. Необходимая норма прибыли составляет 8%. Следует ли принять этот проект?
Решение:
Чистая стоимость проекта равна:
NPV = 55000 (1,08)-1 + 55000 (1,08)-2 + 55000 (1,08)-3 + 55000 (1,08)-4 +
+ 55000 (1,08)-5 - 210000 = 50926 + 47154 + 43661 + 40427 + 37432 – 210000 = 9599 долларов.
Поскольку величина чистой текущей стоимости 9599 долларов, т.е. NPV > 0, то проект может быть принят.
Формулу (18) можно ввести в Excel, тогда можно будет увидеть сумму накопленного дисконтированного денежного потока в каждый год реализации инвестиционного проекта:
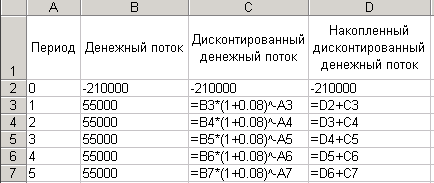
В результате получим:
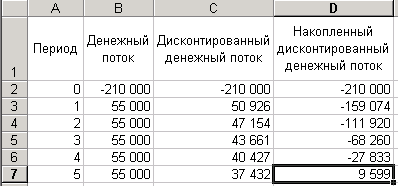
Для проверки правильности ввода формул можно сравнить величину чистой текущей стоимости на 5-й год реализации проекта со значением, рассчитанным вручную (9599 долларов)