Лабораторная работа №5

0. 5.1. Задача о рюкзаке.

Цель работы:

Составить набор компонент a_i, максимизирующий суммарную полезность U при условии∑v_i <= M, где полезностьu_iи вес v_i– характеристики какого-то набора элементов, называемого рюкзаком.

Ход работы:

Самостоятельное задание №8.

Имеется 10 элементов с полезностьюu_iи весомv_iсоответственно (i= 1…10). Составить рюкзак, вес которого не должен превышатьM.

Исходные данные:

u1	u2	U3	u4	u5	u6	u7	u8	u9	u10	v1	v2	v3	v4	v5	v6	v7	v8	v9	v10	M
48	58	29	35	39	56	60	77	61	47	10	9	5	5	4	7	4	10	9	1	17

Решение.

Внесем условия задачи в таблицу Excelв столбцы:

i -номер элемента,

u_i -полезностьi-го элемента

v_i - весi-го элемента.

Включен:1, если элемент включается в рюкзак, и 0, если не включается в рюкзак;

UиV- умножение столбца «Включен» на, соответственно, полезность и весi-го элемента.

В итоге, просуммируем столбцы «U» и «V», получим суммарную полезность и вес включенных в рюкзак элементов.

Для решения задачи воспользуемся функцией Excel«Поиск решения». Необходимо определить, какие элементы должны включаться в рюкзак, то есть какие ячейки в столбце «Включен» должны равняться 1. При этом сумма полезности включенных в рюкзак элементов должна быть максимальной, а сумма весов этих элементов должна быть <= 17.

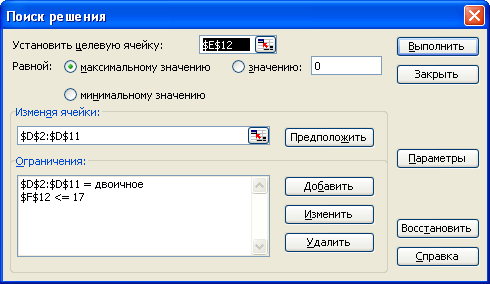
Выполнив поиск решения, получим следующий результат:

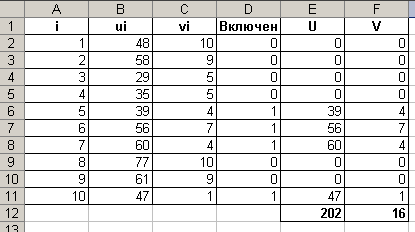
Вывод:

Таким образом, в рюкзак необходимо включить элементы 6,8,10 и 11, при этом вес рюкзака составит 18, а полезность 207.

5.2. Задача о загрузке судна.

Цель работы:

Решить задачу о загрузке, то есть определить каким количеством каждого груза в диапазоне от 0 до m_i, суммарный вес которых ограничен, необходимо загрузить судно, так чтобы получить наибольшую суммарную прибыль.

Ход работы:

Самостоятельное задание №9.

Имеется 5видов различного груза. Количество грузов каждого вида ограничено числомm_i.Каждый груз, помещенный на судно, приносит прибыльu_iи имеет весv_i(i= 1…5). Максимальная грузоподъемность судна равнаM.Определите количествоq_iкаждого вида груза, которым необходимо загрузить судно таким образом, чтобы получить наибольшую суммарную прибыль.

Исходные данные:

m1	m2	m3	m4	m5	u1	u2	u3	u4	u5	v1	v2	v3	v4	v5	M
6	6	3	6	7	56	57	48	63	53	15	16	20	15	14	196

Решение.

Данную задачу решим аналогично предыдущей с той только разницей, что количество помещаемого груза на судно находится в диапазоне от 0 до m_i.

Выполним «Поиск решения» со следующими ограничениями:

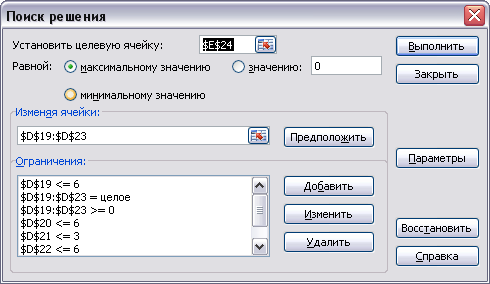
В результате получим:

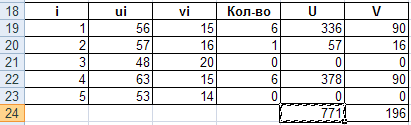
Вывод:Таким образом, чтобы получить наибольшую суммарную прибыль 771 при грузоподъемности судна 196, следует загрузить:

• 1 вид груза в количестве 6;

• 2 вид в количестве 1;

• 3 вид в количестве 0;

• 4 вид в количестве 6

• 5 вид в количестве 0.