1.6. Лабораторная работа №6: Экономико-математическая модель межотраслевого баланса (модель Леонтьева)

В зависимости от цели исследования экономику можно изучать в различных разрезах - от уровня национальной экономики до уровня отдельных фирм и потребителей. Целью построения модели Леонтьева является анализ перетока товаров между отраслями экономики, обеспечивающего такое функционирование производственного сектора, когда объем выпуска соответствует суммарному (т.е. производственному и конечному) спросу на товары. Поэтому экономика рассматривается в разукрупненном до уровня отраслей виде. Предполагается, что каждая отрасль является "чистой", т.е. выпускает только один и только свой продукт. Это допущение и ряд других упрощений (постоянство технологии производства, отсутствие инвестиций, игнорирование невоспроизводимых ресурсов и др.) касаются, в основном, исходной модели. Их не следует относить к недостаткам модели, ибо она в дальнейшем обобщается и конкретизируется до разных уровней детализации.

В модели Леонтьева все отрасли предполагаются взаимозависимыми в том смысле, что для производства своего продукта каждая из них использует результаты производства (продукты) других отраслей и только их. Иначе говоря, на данном уровне формализации применение отраслями невоспроизводимых производственных факторов не предусматривается.

Обозначим через n количество всех отраслей. Так как отрасли являются чистыми, индекс отрасли можно отождествить как с видом товара, так и с технологическим процессом.

Предположим, что на данном плановом периоде времени (например, на предстоящий год) известен конечный спрос y = (y₁,…,y_n)на всеnтоваров. Пусть технология производства предписывает для выпуска одной единицыi-го товараколичество товара вида 1,количество товара вида 2 и т.д. Обозначим черезобъем производства отраслиi на всем плановом периоде (валовый выпуск). Тогда величинаa_ijx_i показывает объем продукции отраслиj, необходимый для функционирования отраслиiс планом выпуска, а величина

- суммарное потребление продукции отрасли iв производственном секторе.

Тогда получаем следующее соотношение баланса, называемого моделью Леонтьева(илимоделью "Затраты-выпуск"):

,i= 1, 2,…,n. (24)

Правую часть равенства (24) можно трактовать как итоговый (производственный плюс конечный) спрос на продукцию отрасли i(наi-ый товар), а левую - как предложениеi-го товара. Поэтому, во-первых, уравнения (24) отражают общее равновесие (т.е. равновесие по всем видам товаров) в экономике. Во-вторых, система (24) показывает самодостаточность производства - для выпуска любого товара достаточно иметь воспроизведенную продукцию рассматриваемых отраслей. В-третьих, из уравнений (24) следует, что весь валовый выпуск полностью распределяется между потребителями. Последние два обстоятельства говорят о замкнутости экономики - нет поступления извне, и продукция не экспортируется.

Таким образом, схема межотраслевого баланса задает те условия, когда экономика будет находиться в равновесном состоянии. А именно, при известном спросе и известной постоянной технологии вектор валового выпуска должен вычисляться как решение системыnлинейных уравнений (24).

Введя вектор валового выпуска X, матрицу прямых затрат A и вектор конечного потребления Y:

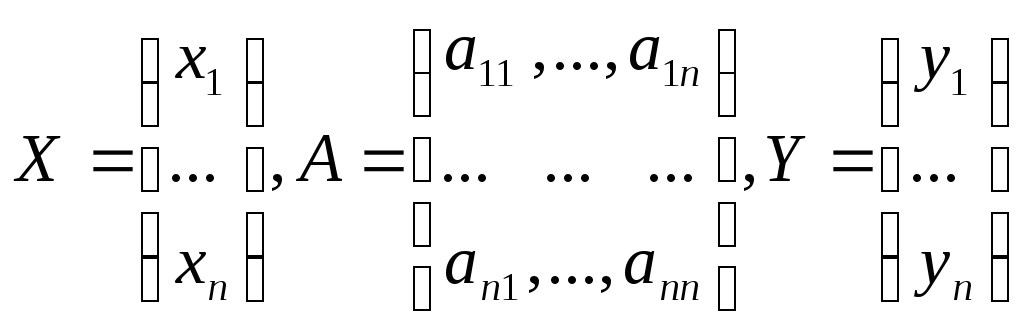
модель Леонтьева (24) можно записать в матричном виде

X=AX+Y(25)

Матрица A ≥ 0, у которой все элементы a_ij≥ 0 (неотрицательны), называется продуктивной матрицей, если существует такой неотрицательный вектор X ≥ 0, для которого выполняется неравенство

X>AX.

Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором продукции выпускается больше, чем затрачивается на ее производство. Другими словами, при этом режиме создается конечный (прибавочный) продукт Y = X – AX> 0.

Модель Леонтьева с продуктивной матрицей Aназывается продуктивной моделью.

Для проверки продуктивности матрицы A достаточно существования обратной матрицы B = (E–A)^-1с неотрицательными элементами, где матрица E – единичная матрица.

С помощью модели Леонтьева (25) можно выполнить три вида плановых расчетов, при условии соблюдения условия продуктивности матрицы A:

1) Зная (или задавая) объемы валовой продукции всех отраслей X можно определить объемы конечной продукции всех отраслей Y:

Y= (E–A)X

2) Задавая величины конечной продукции всех отраслей Yможно определить величины валовой продукции каждой отрасли

X= (E–A)^-1Y(26)

3) Задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.

Матрица B = (E–A)^-1называется матрицей полных материальных затрат. Ее смысл следует из матричного равенства (26), которое можно записать в видеX=BY. Элементы матрицы B показывают, сколько всего необходимо произвести продукции вi-ой отрасли, для выпуска в сферу конечного потребления единицы продукции отраслиj.

Пример.Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

.

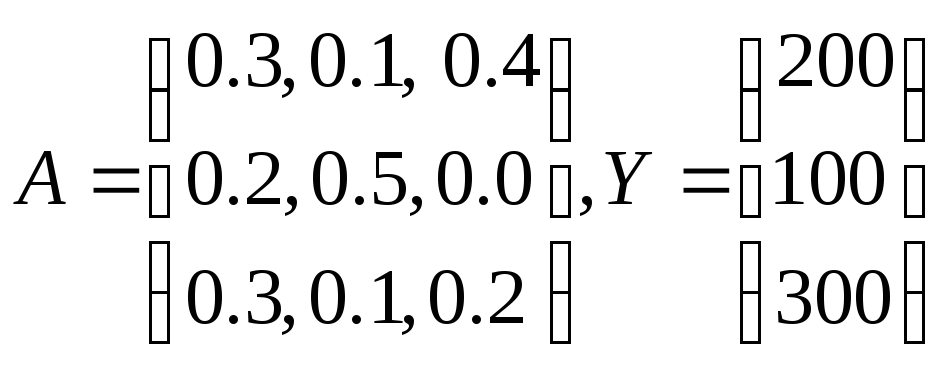Определить:

1) Матрицу коэффициентов полных материальных затрат B

2) Проверить продуктивность матрицы A

2) Вектор валового выпуска X

3) Межотраслевые поставки продукции x_ij

Решение.

Модель Леонтьева имеет вид

X=AX+Y.

Матрица полных материальных затрат Bравна

B = (E–A)^-1

Продуктивность матрицы A проверяется, по вычисленной матрице B. Если эта матрица существует и все ее элементы неотрицательны, то матрица A продуктивна.

Вектор валового выпуска X рассчитывается по формуле

X=BY

Межотраслевые поставки продукции x_ijвычисляются по формуле

x_ij=a_ijx_j

Для решения задачи межотраслевого баланса необходимо уметь выполнять с помощью Excel следующие операции над матрицами:

- Умножение матрицы на вектор

- Умножение двух матриц

- Транспонирование матрицы или вектора

- Сложение двух матриц