2.2.3. Основные характеристики движения жидкостей

Движущей силой при течении жидкости является разность давлений, которая создается с помощью насосов или компрессоров либо вследствие разности уровней или плотностей жидкости.

Знание законов гидродинамики позволяет находить Δp, необходимое для перемещения заданного количества жидкости с требуемой скоростью, а значит, и расход энергии на это перемещение или, наоборот, определить скорость и расход жидкости при заданном Δp.

Различают внутреннюю, внешнюю и смешанную задачи гидродинамики.

К внутренней задаче гидродинамики относятся вопросы изучения закономерностей движения жидкости и газов внутри труб и каналов. Внешняя задача связана с изучением закономерностей обтекания жидкостями и газами различных тел (процессы осаждения, механического перемешивания и т.д.).

Смешанная задача заключается в изучении движения жидкости и газов через зернистые и пористые слои твердых материалов. Жидкость в этом случае движется одновременно внутри каналов сложной формы и обтекает твердые частицы (процессы фильтрования, течения жидкостей и газов через насадки массообменных аппаратов, реакторов с твердым катализатором и т.п.).

Скорость и расход жидкости. Количество жидкости, протекающей через поперечное сечение потока в единицу времени, называется расходом жидкости.

Различают объемный (м³/с) и массовый (кг/с) расходы.

В разных точках поперечного сечения потока скорости частиц жидкости неодинаковы, поэтому в расчетах используют не истинные (локальные) скорости, а фиктивную среднюю скорость: .

Объемный расход жидкости: ,

массовый расход: ,

массовая скорость жидкости: .

Гидравлический радиус и эквивалентный диаметр. При движении жидкости через площадь поперечного сечения любой формы, отличающейся от круглой, в качестве расчетного линейного размера применяют гидравлический радиус или эквивалентный диаметр.

Гидравлический радиус представляет собой отношение площади поперечного сечения трубы или канала, через которое протекает жидкость, к смоченному периметру.

Для круглой трубы .

Диаметр, выраженный через гидравлический радиус, представляет собой эквивалентный диаметр , следовательно,.

Эквивалентный диаметр равен диаметру гипотетического трубопровода круглого сечения, для которого отношение площади F к смоченному периметру П то же, что и для заданного трубопровода некруглого сечения.

Для квадрата со сторонами a и b эквивалентный диаметр

.

Для кольцевого сечения с внутренним диаметром D большого трубопровода и наружным малого d

.

Для круглой трубы .

Установившиеся и неустановившиеся потоки. Движение жидкости называется установившимся или стационарным, если скорости частиц потока и другие параметры, влияющие на его движение, например ,р, Т, не изменяются во времени в каждой фиксированной точке пространства. Расходы жидкости при установившемся течении через поперечные сечения канала также не зависят от времени.

При установившемся движении жидкости проекция скорости может быть переменной в любой из точек, но не меняется со временем, т.е..

В отличие от стационарного при неустановившемся или нестационарном потоке факторы, влияющие на движение жидкости, изменяются во времени:

, т.е. .

Установившиеся условия движения жидкости характерны для непрерывных процессов химической технологии. Неустановившееся течение жидкости происходит главным образом в периодических процессах или возникает кратковременно в непрерывных процессах в период пуска или изменения режима работы установки.

Для каждой движущейся частицы жидкости изменение ее параметров во времени и пространстве выражается не частной, а полной производной во времени, называемой в гидродинамике субстанциональной производной. По смыслу ее называют производной, следующей за потоком.

Обозначим через любую величину, изменяющуюся в потоке жидкости как во времени, так и в пространстве, например: плотность, давление, температуру, концентрацию или любую из составляющих скоростижидкости в направлении осей координат.

Допустим, что при наблюдении за движением потока можно мгновенно регистрировать значение параметра в каждый момент времени и в любой точке потока. Изменение параметрав единицу времени для фиксированной точки пространствавыражается частной производной, а изменениев указанной точке за бесконечно малый промежуток временисоставляет. Это изменение являетсяместным или локальным изменением данной переменной. При установившемся движении .

Если наблюдатель перемещается вместе с потоком, с какой-либо частицей, то за время частица потока переместится из точкиА с координатами в точкуВ с координатами ,и.

В результате перемещения из точки А в точку В изменения , соответствующие проекциям пути, равны,и. Эти изменения не связаны с изменениемво времени в какой-либо фиксированной точке пространства. Если бы не было локального изменения, то при переходе частицы из точкиА в точку В значение изменилось бы на величину

.

Это выражение представляет собой конвективное изменение параметра . Полное изменениепри неустановившемся движении представляет собой суммулокального и конвективного изменений

,

откуда изменение параметра за малый промежуток времени

, ,,,

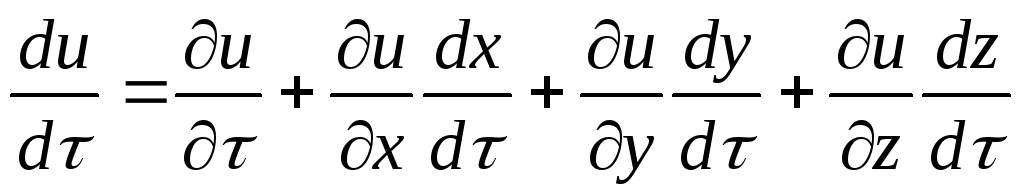тогда .

При установившемся движении ,.

Последние выражения представляют собой субстанциональную производную для неустановившегося и установившегося течения жидкости. Они характеризуют изменение какого-либо параметра или свойства материи (субстанции) во времени при перемещении материальных частиц в пространстве. С учетом специфики понятия субстанциональную производную зачастую обозначают вместо.