2.2.4. Уравнение неразрывности (сплошности) потока

Это уравнение представляет собой зависимость между скоростями в потоке жидкости, для которого соблюдается условие сплошности, или неразрывности течения, т.е. в жидкости не образуется незаполненных пустот.

Уравнение выражает фундаментальный закон сохранения массы (расхода).

Дифференциальное уравнение неразрывности для неустановившегося течения имеет вид

В установившемся потоке плотность не меняется во времени , поэтому уравнение неразрывности выглядит так:

Для капельных жидкостей, которые практически несжимаемы, а также для газов в условиях изотермического потока при скоростях, меньших скорости звука, , следовательно, уравнение неразрывности примет вид

Для трубопровода постоянного сечения в результате интегрирования дифференциального уравнения неразрывности для установившегося однонаправленного движения жидкости (в направлении оси ) получается зависимость

.

Если же площадь сечения трубопровода переменна, то интегрирование по площади приводит к зависимости

. (2.4)

Для трех сечений трубопровода одного и того же потока жидкости (рис. 2.6):

или для массового расхода жидкости в трубопроводе переменного сечения:

.

Согласно уравнению постоянства расхода, при установившемся течении жидкости, полностью заполняющей трубопровод, через каждое его поперечное сечение проходит в единицу времени одно и то же количество жидкости

,

при

(2.5)

или для объемного расхода жидкости в трубопроводе переменного сечения

.

Из уравнения (2.5) следует, что скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений.

В соответствии с уравнением (2.4), массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода (рис. 2.6). Таким образом, уравнение неразрывности является частным случаем закона сохранения массы и выражает материальный баланс потока.

2.2.5. Режимы движения жидкостей

Характер движения жидкости зависит от скорости ее течения. Этот вопрос был решен в 1883 г. О. Рейнольдсом, который поставил простой убедительный опыт. Установка О. Рейнольдса показана на рис. 2.7. Характер движения жидкости устанавливается по степени размытости струйки подкрашенной жидкости, истекающей по трубке 2 из сосуда 1. В зависимости от высоты уровня жидкости в сосуде 1 устанавливалась та или иная скорость течения.

При малых скоростях течения струя окрашенной жидкости 3 не размывалась, что указывало на послойный характер движения жидкости. Такие течения были названы ламинарными.

Рис. 2.7. Опыт Рейнольдса:

а – ламинарное движение; б – турбулентное движение

При некоторой критической скорости струйка размывалась по всему сечению, что свидетельствовало о вихревом характере перемешивания жидкости по всему сечению трубы 4. Такой режим течения был назван турбулентным. Рейнольдс показал, что переход от одного режима течения к другому соответствует определенному значению безразмерной величины:

,

где – средняя скорость;– диаметр канала;– кинематический коэффициент вязкости жидкости.

Безразмерная переменная впоследствии была названа числом или критерием Рейнольдса. Переход от ламинарного течения наступает при . Причаще всего наблюдается турбулентный режим течения. Однако прирежим течения неустойчиво турбулентный, илипереходный.

Вышесказанное справедливо к стабилизированным изотермическим потокам в прямых трубах с малой шероховатостью стенок. Наличие различных возмущений, обусловленных шероховатостью стенок трубы, изменением скорости или направления течения потока, близость входа в трубу и т. п. могут существенно снизить значения критических чисел Рейнольдса.

Распределение скоростей в движущемся потоке жидкости. Распределение скоростей определяется режимом течения жидкости. При ламинарном режиме распределение может быть установлено законом Стокса

,

представляющим параболическое распределение скоростей в сечении трубопровода, где – текущий радиус, отсчитываемый от оси трубопровода;– скорость на оси трубопровода.

Средняя скорость по сечению трубопровода связана с максимальной скоростью следующим соотношением

.

Уравнение, определяющее объемный расход жидкости при ее ламинарном движении в круглой прямой трубе, носит название уравнения Пуазейля

.
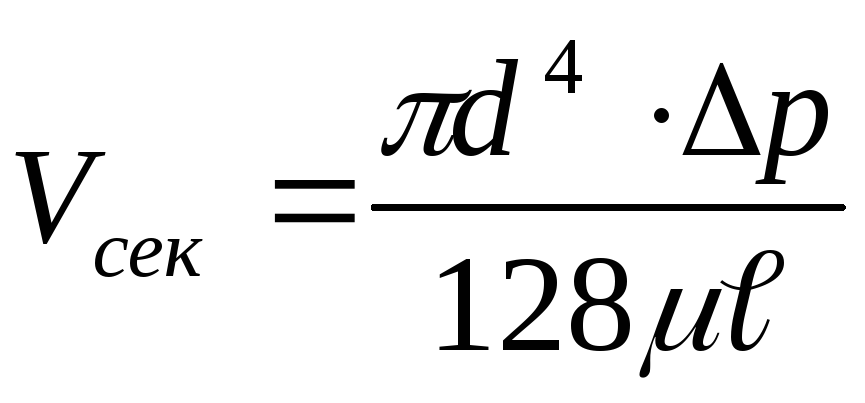