Диагонализации квадратичной формы ортогональным преобразованием координат

Поскольку - ортогональна матрица, то есть также равенство:

А это формула изменения матрицы квадратичного функционала при переходе к новому базису. Напомним, что квадратичный функционал всегда имеет симметричную матрицу. Координатное представление квадратичного функционала -квадратичная форма.

Теорема. Для любого квадратичного функционала существует ортогональный базис , в котором матрица этого функционала является диагональной.

Любую квадратичную форму можно ортогональным преобразованием координат привести к диагональному виду.

Пусть - квадратичная форма.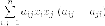

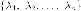 - Собственные числа симметричной матрицы квадратичной формы. Собственно число выписано столько раз, какова его кратность.

- ортонормированный базис из собственных векторов (собственный вектор 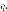соответствует собственному числу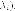 

 - матрица перехода к новому базису, й столбик матрицы- это координаты вектора

Если 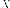столбик старых координат,столбик новых координат, то после преобразования координатимеем:

То есть матрица квадратичной формы в новых координатах:

Приведение общего уравнения кривой

Приведение общего уравнения кривой второго порядка к каноническому виду

Общее уравнение кривой второго порядка имеет вид:

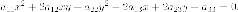
Квадратичная часть этого уравнения  - это квадратичная форма

Матрица квадратичной формы:

В каноническом уравнении матрица квадратичной части должно быть диагональной. Нам известно, что существует ортогональное преобразование координат такое, что матрица квадратичной формы в новых координатах имеет диагональный вид. Новый базис образуется из собственных векторов матрицы

Итак, для того чтоб привести общее уравнение к каноническому виду нужно

• найти ортогональный базис из собственных векторов матрицы;

• перейти к новой системе координат, в которой матрица квадратичной части является диагональной;

• осуществить параллельный перенос начала координат таким образом, чтобы уравнение приняло канонический вид (например, в центр вершину кривой).

Пример . Привести к каноническому виду уравнение кривой

Найти каноническую систему координат.

Выписываем матрицу квадратичной части:

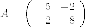
Характеристический многочлен этой матрицы:

Его корни, собственные числа матрицы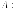 

Ищем собственные векторы.

Для собственный вектор находится из системы уравнений Матрица этой системы:

Итак, собственный вектор имеет направление 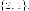Нормируем его (делим на длину) и берем в качестве первого нового базисного вектора 

Для собственный вектор находится из системы уравнений Матрица этой системы:

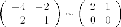
Итак, собственный вектор имеет направление Нормируем его (делим на длину) и берем в качестве второго нового базисного вектора 

Переходим к новой системе координат. Напомним, что старые координаты 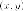связаны с новымиследующим образом:

где - матрица перехода к новому базису, ее столбиками есть координаты новых базисных векторов в старом базисе.

Матрица - ортогональная, ее определитель равен илиВ нашем случаеесть при таком преобразовании координат мы изменим ориентацию плоскости, не желательно. Итак, для того чтобыориентация не изменилась, мы изменим направление нового второго базового вектора на противоположный, то есть возьмем 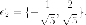Итак

Преобразование координат

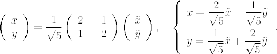
Подставляем эти выражения в уравнение кривой. В квадратичную часть подставлять не нужно, по известной теореме в базисе из собственных векторов матрица квадратичной части имеет диагональный вид, где диагонали стоят собственные числа. Нужно подставить эти выражения только в линейную часть:

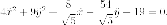
Выделяем полные квадраты:

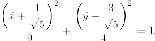
Делаем замену переменных, с геометрической точки зрения  - параллельный перенос:

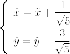
В новой системе координат имеем каноническое уравнение эллипса :

Теперь нужно выписать общее преобразование координат. Выражаем координаты 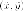через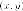

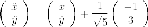
i подставляем в выражение для координат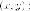 

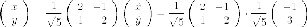
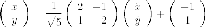
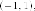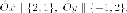Итак, это превращение дает нам каноническую систему координат: ее начало находится в точке с координатаминаправляющие векторы новых координатных осей(направляющий вектор - это не базовый вектор, он может быть не единичным).

Приведение общего уравнения поверхности