• 1. - Эллипс ,

• 2.  - воображаемый эллипс,

• 3.  - гипербола,

• 4.  - парабола ,

• 5.  - пара прямых, которые пересекаются,

• 6.  - пара мнимых прямых, которые пересекаются,

• 7. - пара параллельных прямых  ,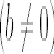

• 8. - пара параллельных воображаемых прямых ,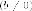

• 9.  - пара прямых, совпадают.

• Некоторые способы образования поверхностей

• Цилиндрические поверхности

• Пусть - плоская кривая, то есть лежит в плоскости Через каждую точку кривой проведём прямую в направлении вектора который не параллелен плоскости Полученная поверхность называется цилиндром , построенным над Сама кривая называется направляющей , а семья параллельных прямых называется семье образующих цилиндра. 

• Можно записать параметрическое уравнение цилиндрической поверхности. Пусть кривая имеет параметрическое (векторное) уравнениеПри фиксированном значениимы точку наНапишем параметрическое уравнение прямой через точку в направлении вектора 

• 

• Это параметрическое уравнение цилиндрической поверхности с направляющей и прямолинейными образующими параллельнымиВекторное уравнение этой поверхности

• Если прямолинейные образующие перпендикулярны плоскости в которой лежит криваято поверхность называется прямым цилиндром, построенным надПо типу направляющей цилиндрам дают соответствующие названия. Например, "прямой круговой цилиндр"- цилиндр, построенный над кругом.

• Уравнение прямого цилиндра задать очень легко. Расположим в плоскости оси координат, а осьнаправим перпендикулярноесть вдоль образующих цилиндра. Пусть- неявное уравнение кривой Тогда для любой точки с координатами на цилиндрической поверхности, координаты связаны соотношением  а координата является произвольной, то есть уравнение поверхности формально совпадает с уравнением кривой:

• 

• это неявное уравнение прямого цилиндра.

• Поверхности вращения

• Пусть - кривая в некоторой плоскости и - прямая, лежащая в плоскости и не пересекает поверхность которая образуется кривой при вращении плоскости вокруг прямой называется поверхностью вращения. Кривая называется профильной кривой , - осью вращения .

• Запишем параметрическое уравнение поверхности вращения. Примем прямую как осьа вотнаправим перпендикулярно осив плоскостилежит криваяВотнаправим перпендикулярноПредположим, чтозадана уравнениемВ начальный момент плоскостьсовпадает сВернем плоскостьна некоторый уголфиксируя положение осейи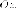для любой точкикоординатапри этом не изменится. Не изменится ирасстояние от оси вращенияк новому положению точкиесть при каждом фиксированном значениипри вращении плоскостивокруг оситочкакоторая в начальный момент имела координатыдвижется по окружности радиусав плоскостиПараметрическое уравнение кругаИтакпараметрическое уравнение поверхности вращения :

• 

• Уравнение поверхности вращения получить особенно легко, если кривая может быть задана в виде графика некоторой функции. Предположим, чтолежит в плоскостии задана уравнениемПри вращении вокруг осикоординаталюбой точкипри этом не изменится. Не изменится ирасстояние от оси вращенияк новому положению точки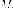Следовательно, уравнение которое связывает координаты точек поверхности примет вид: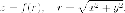

• 

• Следствие. Если - неявное уравнение кривой, которая лежит в плоскости то

• 

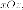
• неявное уравнение поверхности вращения вокруг оси

• Пример. Прямая вращается вокруг осиНайдите уравнение поверхности вращения.

• При вращении вокруг оси точкас координатамидвижется по кругу, которое лежит в плоскостии имеет центр в точкеНайдем радиус кругаНапишем параметрическое уравнение поверхности вращения:

• 

• Мы получили неявное уравнение этой же поверхности. В разделе "гиперболоиды" мы выясним, что это однополостный гиперболоид вращения с центром в точке 

• 

• Поверхности переноса.

• Рассмотрим плоскость и пусть криваяЗафиксируем точкуи построим плоскостьпересекающей плоскостьпо прямойпроходящей через точкуПустьнекоторая кривая в плоскостипричем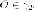Фиксируя плоско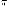стьбудем параллельно переносить плоскостькак твердое тело, вдоль кривойтак, чтобы точкапри движении находилась на кривойповерхность образована кривойназываетсяповерхностью переноса .

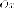• Уравнение поверхности переноса легче получить если плоскости ивзаимно перпендикулярны. Примем прямуюкак осьи осиинаправим в плоскостяхиПредположим, что уравнениеа уравнениеТогда координататочкина поверхности переноса состоит из координатыв плоскостинад осьюи координатыточкинад осьюв плоскостиесть координатадвижущейся точки определяется выражением:

• 

Эллипсоиды.

 В плоскости 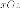возьмем эллипс

и будем вращать его вокруг оси получим поверхность с уравнением

которая называется эллипсоидом вращения .

Итак, эллипсоид вращения получается вращением канонического эллипса вокруг меньшей полуоси.

Если мы будем проводить сжатие пространства вдоль оси с коэффициентомто с эллипсоида вращения мы получим так называемыйтрехосный эллипсоид :

Действительно, если точка с координатамилежит на эллипсоиде вращения

то точка 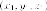с координатамина поверхности эллипсоида

Трехосный эллипсоид выходит из эллипсоида вращения сжатием вдоль оси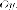 

И так имеем такое

Определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

называется эллипсоидом. Данное уравнение называется каноническим уравнением эллипсоида, а соответствующая система координат называется канонической. Если то поверхность называетсяэллипсоидом вращения.

(Случай мы не рассматриваем, - в этом случае поверхность является сферой.)

Замечания. Уравнение

определяет пустую множество в пространстве, но по аналогии с эллипсоидом говорят, что это уравнение задает воображаемый эллипсоид.

Эллипсоид имеет три плоскости симметрии - координатные плоскости, три оси симметрии  - оси координат и единый центр симметрии  - начало координат.

Рассмотрим  сечения эллипсоида плоскостями вида В проекции на плоскость получим  семью эллипсов

с полуосями 

Сечения существуют при   Аналогично по другим осям.

Пример. Даны вершины эллипсоида Найдите уравнение этого эллипсоида, то если известно, что его оси симметрии параллельные осям координат и плоскость пересекает его по эллипсу: 

Известно, что вершины находятся на оси симметрии, а центр эллипсоида расположен посередине между вершинами. Итак, - ось симметрии, -центр симметрии.

Заметим, что если оси симметрии эллипсоида параллельные осям координат, а центр имеет координаты то уравнение эллипсоида имеет вид:

В нашем случае:

Параметр - это расстояние от центра до вершин, то есть Подставляем это значение в уравнение эллипсоида и находим пересечение с плоскостью 

Сравниваем это уравнение с известным, получаем:

Следовательно, уравнение эллипсоида:

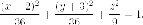
Круговые сечения трехосного эллипсоида.

Заметим, что на каноническом эллипсоиде

сечение  дает эллипс с большой полуосью на оси а сечение  дает эллипс с малой полуосью на оси Итак, существует сечение, где полуоси уровне и равны

Рассмотрим плоскость,  натянутую на векторы:

которая проходит через начало координат. Векторное уравнение этой плоскости: Векторы перпендикулярны и имеют единичную длину, поэтому в плоскости векторы и образуют базисные векторы декартовой прямоугольной системы координат. Итак, - координаты относительно этой системы координат. Запишем параметрическое уравнение плоскости   

и найдем ее пересечение с эллипсоидом:

или 

В плоскости сечения параметры и есть декартовыми прямоугольными координатами. Поэтому полученный сечение является эллипсом. Покажем, что среди этих эллипсов является круг. Будем подбирать так, чтобы

Итак, 

Действительно, 

Упражнение. Показать, что любая плоскость параллельна найденной, пересекает эллипсоид по кругам.

Точка на эллипсоиде, в которой касательная плоскость параллельна круговым сечениям называется оболочною точкой, или коротко ОМБИЛИК .

Упражнение. Найти омбиличны точки на поверхности трехосного эллипсоида. Исследовать их поведение в зависимости от соотношения осей.

Гиперболоиды.

Однополостный гиперболоид

В плоскости 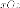возьмем гиперболу

и будем вращать ее вокруг оси получим поверхность с уравнением

которая называется Однополостный гиперболоидом вращения .

Итак, однополостный гиперболоид вращения получается вращением гиперболы вокруг воображаемой оси.

Если мы будем проводить сжатие пространства вдоль оси с коэффициентомто с однополостного гиперболоида вращения мы получим так называемыйтрехосный однополостный гиперболоид :

Итак имеем такое  определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

называется Однополостный гиперболоидом . Данное уравнение называется каноническим уравнением однополостного гиперболоида, а соответствующая система координат называется канонической . Если то поверхность называетсяОднополостный гиперболоидом вращения .

Однополостный гиперболоид имеет три плоскости симметрии  - координатные плоскости, три оси симметрии  - оси координат и единый центр симметрии  -начало координат.

Сечения однополостного гиперболоида плоскостями проецируются на плоскостьв  семью эллипсов

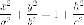
с полуосями 

Сечения однополостного гиперболоида плоскостями проецируются на плоскость

• при 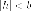в семью гипербол 

с полуосями  

• при в пару прямых, пересекающихся 

• при в самосопряжённых гипербол 

с полуосями 

Свойства сечений плоскостями аналогичные свойствам сечений плоскостями

Двуполостные гиперболоид.

В плоскости возьмем сопряженную гиперболу

и будем вращать ее вокруг оси получим поверхность с уравнением

которая называется двуполостные гиперболоидом вращения .

Итак, двуполостные гиперболоид вращения получается вращением гиперболы вокруг действительной оси.

Если мы будем проводить сжатие пространства вдоль оси с коэффициентомто с двуполостные гиперболоида вращения мы получим так называемыйтрехосный двуполостные гиперболоид :

Итак имеем такое

Определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

называется двуполостные гиперболоидом. Данное уравнение называется каноническим уравнением двуполостные гиперболоида, а соответствующая система координат называется канонической. Если то поверхность называетсядвуполостные гиперболоидом вращения.

Двуполостные гиперболоид имеет три плоскости симметрии - координатные плоскости, три оси симметрии  - оси координат и единый центр симметрии  -начало координат.

Сечения двуполостные гиперболоида плоскостями 

• при проецируются на плоскостьв семью эллипсов

с полуосями 

• при плоскостьсоприкасается поверхности в единой точке- вершине 

• при плоскостьне имеет общих точек с двуполостные гиперболоидом.

Сечения двуполостные гиперболоида плоскостями проецируются на плоскостьв  семью гипербол

с полуосями 

Свойства сечений плоскостями аналогичные свойствам сечений плоскостями

Упражнение. Найти круговые сечения трехосного двуполостные гиперболоида и омбилични точки на нем. Исследовать поведение омбиличних точек в зависимости от соотношения осей.

Параболоид.

Эллиптический параболоид.

В плоскости возьмем параболу

и будем вращать ее вокруг оси получим поверхность с уравнением

которая называется параболоидом вращения.

Эллиптический параболоид

получается из параболоида вращения сжатием вдоль оси 

Определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

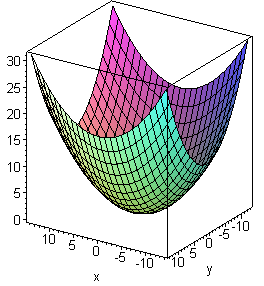
называется эллиптическим параболоидом . Данное уравнение называется каноническим уравнением эллиптического параболоида, а соответствующая система координат называется канонической . Если то поверхность называетсяэллиптическим параболоидом вращения , или просто параболоидом вращения.

Эллиптический параболоид имеет две плоскости симметрии  - координатные плоскости иодну ось симметрии - ось и не имеет ни центра симметрии.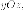  

Сечения эллиптического параболоида плоскостями 

• при проецируются на плоскостьв  семью эллипсов 

с полуосями  

• при плоскостьсоприкасается поверхности в единой точкекоторая называется вершиной эллиптического параболоида;

• при плоскостьне имеет общих точек с эллиптическим параболоидом.

Сечения эллиптического параболоида плоскостями проецируются на плоскостьв  семью конгруэнтных парабол

полученные сдвигом "вверх" параболы 

Свойства сечений эллиптического параболоида плоскостями аналогичные свойствам сечений плоскостями

Эллиптический параболоид является поверхностью переноса, образованной парабола мы икоторые лежат во взаимно ортогональных координатных плоскостях.

Гиперболический параболоид.

Еще одной поверхностью переноса второго порядка является гиперболический параболоид, он образуется парабола мы 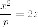икоторые лежат во взаимно ортогональных координатных плоскостях.

Определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

называется гиперболическим параболоидом . Данное уравнение называется каноническим уравнением гиперболического параболоида, а соответствующая система координат называется канонической .

Гиперболический параболоид имеет две плоскости симметрии  - координатные плоскости иодну ось симметрии - ось и не имеет ни центра симметрии.  

Сечения гиперболического параболоида плоскостями проецируются на плоскость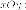 

• при в сім'ю гіпербол 

с полуосями 

• при в две прямые, пересекающиеся 

• при в сім'ю гіпербол 

с полуосями 

Сечения эллиптического параболоида плоскостями проецируются на плоскостьв  семью конгруэнтных парабол

полученные сдвигом "вниз" параболы 

Сечения эллиптического параболоида плоскостями проецируются на плоскостьв  семью конгруэнтных парабол

полученные сдвигом "вверх" параболы 

Конусы и цилиндры

Шишки

В плоскости возьмем две прямые, пересекающиеся

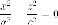
и будем вращать их вокруг оси получим поверхность с уравнением

которая называется конусом вращения .

Тривісний конус

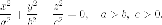
получается из конуса вращения сжатием вдоль оси с коэффициентом 

Определение. Геометрическое место точек пространства, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяет уравнению

называется конусом . Данное уравнение называется каноническим уравнениемконуса, а соответствующая система координат называется канонической . Если то поверхность называетсяконусом вращения.

Замечания. Уравнение

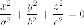
определяет одну точку  - начало координат, но по аналогии с конусом говорят, что это уравнение задает воображаемый конус с вершиной в настоящей точке 

Конус имеет три плоскости симметрии  - координатные плоскости, три оси симметрии  - оси координат и единый центр симметрии  - начало координат.

Сечения конуса плоскостями проецируются на плоскостьв семейство эллипсов

с полуосями 

При эллипсы вырождаются в точку с координатамикоторая называетсявершиной конуса.

Сечения конуса плоскостями проецируются на плоскость 

• при 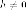в семейство гипербол

с полуосями 

• при в две прямые, пересекающиеся 

Свойства сечений плоскостями аналогичные свойствам сечений