
- •Парабола.
- •Директориальна свойство параболы
- •Относился к притче.
- •Оптическая свойство параболы.
- •Фокусное свойство эллипса
- •Директориальна свойство эллипса
- •Уравнение касательной к эллипсу
- •Оптическая свойство эллипса
- •Фокусное свойство гиперболы
- •Директориальна свойство гиперболы
- •Уравнение касательной к гиперболе.
- •Оптическая свойство гиперболы.
- •Поверхности вращения
- •Поверхности переноса.
- •Цилиндры.
- •Прямолинейные образующие на поверхности однополостного гиперболоида
- •Прямолинейные образующие на поверхности гиперболического параболоида
- •Касательная плоскость
- •Свойства симметричной матрицы
- •Самосопряжённых оператор в евклидовом пространстве
- •Диагонализации квадратичной формы ортогональным преобразованием координат
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •Приведение общего уравнения поверхности второго порядка к каноническому виду
Свойства симметричной матрицы
Матрица  будет
симметричной тогда и только тогда, когда
для любых вектор-столбцов
будет
симметричной тогда и только тогда, когда
для любых вектор-столбцов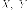 выполняется
выполняется

Действительно,
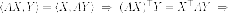
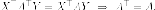
Утверждение. Если - симметричная
матрица с действительными элементами
размера тогда все собственные числа
матрицы действительны.
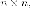

Доказательство. Пусть - собственное
число матрицы - вiдповидний
собственный вектор, т.е.
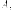
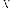

Рассмотрим
вектор-столбец  с
комплексно сопряженными координатами,
принимая во внимание, что матрица
с
комплексно сопряженными координатами,
принимая во внимание, что матрица имеет
действительные элементы (
имеет
действительные элементы ( ):
):
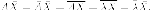
Итак,
вектор-столбец 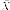 является
собственным вектором
матрицы
является
собственным вектором
матрицы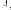 соответствующий
собственному числу
соответствующий
собственному числу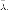 Мы
два равенства:
Мы
два равенства:

Поскольку
матрица  симметрична,
то
симметрична,
то

Итак, имеем:
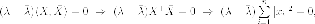
и
так как 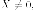 то
то 
Утверждение. Собственные
векторы симметричной
матрицы 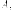 соответствующие
различным собственным числам взаимно
ортогональны.
соответствующие
различным собственным числам взаимно
ортогональны.
Доказательство. Пусть 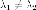 -
различные собственные числа
матрицы-собственные
векторы, которые им соответствуют, то
есть
-
различные собственные числа
матрицы-собственные
векторы, которые им соответствуют, то
есть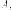


Тогда, 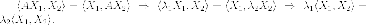
Отнимая, получаем
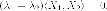
Поскольку 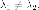 то
то 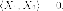
Самосопряжённых оператор в евклидовом пространстве
Пусть линейный
оператор ,
которому в ортонормированном
базисе отвечает матрица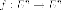
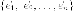
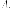
Оператор 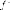 называетсясопряженным
к оператору
называетсясопряженным
к оператору 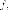 если
для любых векторов
если
для любых векторов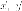 выполняется
выполняется

Выясним
какая матрица соответствует сопряженное
оператору. Если  -
матрица оператора
-
матрица оператора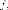 а
матрица- матрица
сопряженного оператора то
имеем
а
матрица- матрица
сопряженного оператора то
имеем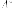
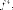
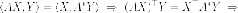
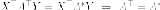
Итак сопряженных оператору соответствует транспонированная матрица .
Оператор
называется самоспряжених ,
если самоспряжених
оператору соответствует симметричная
матрица

Собственные
числа матрицы - это
собственные значения оператора и
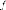

где
вектор-столбец 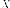 соответствует
вектору
соответствует
вектору
Поскольку между линейными операторами и их матрицами в некотором базисе существует изоморфизм, то свойства собственных чисел и собственных векторов симметричной матрицы являются свойствами собственных чисел и собственных векторов самосопряжённого линейного оператора.
Утверждение.
Пусть 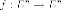 самосопряжённыхлинейный
оператор ,
тогда все собственные числа
самосопряжённыхлинейный
оператор ,
тогда все собственные числа 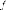 действительны,
а собственные векторы, соответствующие
различным собственным числам, ортогональны.
действительны,
а собственные векторы, соответствующие
различным собственным числам, ортогональны.
Итак,
если все собственные числа самосопряжённого
линейного оператора разные, тогда в
евклидовом пространстве
существует ортонормированный
базис 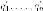 из
собственных векторов этого оператора.
из
собственных векторов этого оператора.
Действительно,
мы имеем  различных
действительных собственных чисел,
каждому из них соответствует ненулевой
собственный вектор. Все собственные
векторы между собой ортогональны,
нормируем их и получаем орто \ -нор \
-мований базис
различных
действительных собственных чисел,
каждому из них соответствует ненулевой
собственный вектор. Все собственные
векторы между собой ортогональны,
нормируем их и получаем орто \ -нор \
-мований базис
Остается
вопрос, что происходит, если собственное
число как корень характеристического
полинома имеет кратность больше
единицы? Оказывается, что размерность
подпространства собственных векторов,
соответствующих собственному
числу 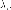 равна
кратности корня
равна
кратности корня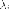 в
характеристическом полиноме. Наша
задача доказать, что для самосопряжённого
оператора существуетортогональный
базис из
собственных векторов.
в
характеристическом полиноме. Наша
задача доказать, что для самосопряжённого
оператора существуетортогональный
базис из
собственных векторов.
Напомним,
что подпространство 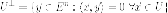 называется
ортогональным
дополнением подпространства
называется
ортогональным
дополнением подпространства  подпространства
подпространства и
и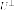 образуют
прямую сумму
образуют
прямую сумму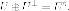
Лема. Пусть 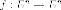 самосопряжённыхлинейный
оператор ,
самосопряжённыхлинейный
оператор ,  -
инвариантный подпространство в отношении
этого оператора, то есть
-
инвариантный подпространство в отношении
этого оператора, то есть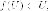 тогда
ортогональное дополнение
тогда
ортогональное дополнение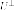 также
инвариантным подпространством
относительно
также
инвариантным подпространством
относительно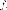
Доказательство. По определениями ортогонального дополнения, инвариантного подпространства и самосопряжённого оператора имеем:
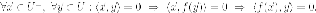
Итак, имеем
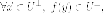
что
означает, что 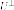 есть
инвариантным подпространством
относительно
есть
инвариантным подпространством
относительно 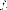
Теорема . Пусть 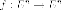 самосопряжённыхлинейный
оператор ,
тогда в пространстве существует ортонормированный
базис из
собственных векторов оператора
самосопряжённыхлинейный
оператор ,
тогда в пространстве существует ортонормированный
базис из
собственных векторов оператора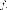
Доведения.
Все собственные числа самосопряжённого
оператора действительны. Пусть - различные
собственные числа кратность которых
в характеристическом полиноме может
быть больше единицы.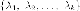
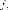
Пусть - соответствующие
собственные подпространства
(подпространства из собственных
векторов). Доказано, что эти
подпространства между собой ортогональны,
так что они образуют прямую сумму.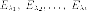
Докажем, что

Предположим обратное
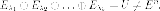
Подпространство  состоит
из собственных векторов
состоит
из собственных векторов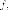 следовательно
он инвариантным подпространство
водноосно этого
оператора, по лемме ортогональное
дополнение
следовательно
он инвариантным подпространство
водноосно этого
оператора, по лемме ортогональное
дополнение 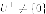 также
инвариантным подпространством
относительно
также
инвариантным подпространством
относительно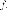 Рассмотрим
ограничения
Рассмотрим
ограничения самосопряжённого
линейного оператора
самосопряжённого
линейного оператора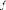 на
инвариантный подпространство
на
инвариантный подпространство 
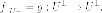
Два
оператора  и
и отличаются
лишь областью определения. Итак
оператор
отличаются
лишь областью определения. Итак
оператор также
самосопряжённых, он действует на
ненулевом пространстве, следовательно
имеет хотя бы одно собственное
число
также
самосопряжённых, он действует на
ненулевом пространстве, следовательно
имеет хотя бы одно собственное
число 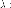

Но 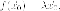 значит
значит является
собственным числомоператора
является
собственным числомоператора 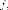 а
а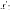 является
собственным
вектором
является
собственным
вектором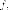 есть
есть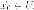 С
С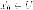 и
и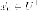 следует,
что
следует,
что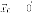 -
противоречие. Итак,
-
противоречие. Итак, есть
есть

В
каждом из подпространств 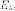 мы
можем выбратьортогональный
базис и
получить ортогональный
базис всего
пространства
мы
можем выбратьортогональный
базис и
получить ортогональный
базис всего
пространства 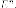 Теорема
доказана.
Теорема
доказана.
Так
что для самосопряжённого оператора
существует ортогональный
базис из
собственных векторов и матрица оператора
в этом базисе имеет диагональный вид.
Напомним, что матрица перехода  (ее столбики- это
координаты новых базисно их векторов)
от ортонормированного базиса к
ортонормированного является ортогональной:
(ее столбики- это
координаты новых базисно их векторов)
от ортонормированного базиса к
ортонормированного является ортогональной:
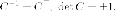
Если - симметричная
матрица самосопряжённого линейного
оператора в некотором базисе, - матрица
перехода к ортонормированного базиса
из собственных векторов то в новом
базисе мы диагональную
матрицу



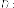
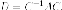
Благодаря изоморфизма между линейными операторами и матрицами мы имеем такую теорему.
Теорема. Для
любой симметричной матрицы  с
действительными элементами
размера
с
действительными элементами
размера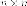 существует
ортогональная матрица
существует
ортогональная матрица такая,
что
такая,
что
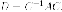
где - диагонально
матрица с действительными элементами.
Или короче, любая симметричная матрица ортогонально подобная диагональной .
