Оптическая свойство параболы.

Утверждение. Касательная к параболе образует равные углы с осью 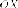и с фокальным радиусом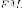

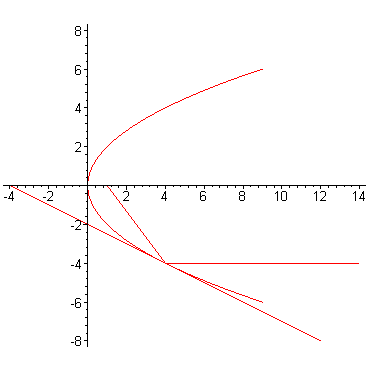
Доказательство. Обозначим через - точку пересечения касательной с осью   Из уравнения касательной следует, что ее координаты Итак, Таким образом, треугольник равнобедренный.

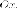
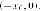
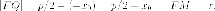
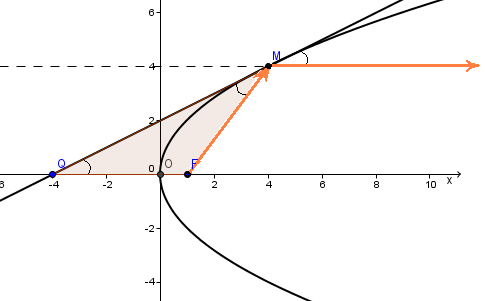
Если представить параболу как зеркальную кривую, то по законам оптики луч света, выпущенный из фокуса, после отражения от параболы пойдет на бесконечность параллельно фокальной оси. И наоборот, пучок лучей, параллельных фокальной оси, соберется в фокусе. Собственно, по этой причине указанное свойство называется оптической. Фокусное ось иногда называется оптической осью параболы. Оптическая свойство имеет очевидные технические применения.

Эллипс.

Г.М.Т, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяют уравнению

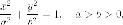
называется эллипсом . Данное уравнение называется каноническим уравнением эллипса , а соответствующая система координат называется канонической .

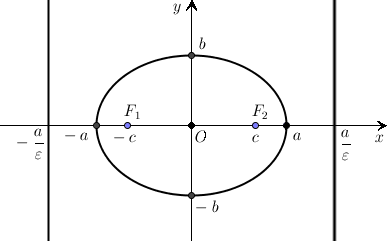
Геометрическими характеристиками эллипса являются:

• две оси симм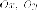етрии и одинцентр симметрии  ;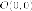

• Величины и, которые называются соответственнобольшой и малой полуосями;

• величина 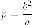, которая называетсяфокальным параметром ;

• величина ;

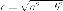• точки 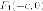и, которые называютсялевым и правым фокусами (очаговыми точками) соответственно;

• величина 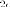, которая называетсяфокусным расстоянием ;

• величина 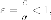которая называетсяэксцентриситетом ;

• две директрисы :

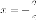 - левая, или 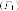 директриса,

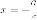 - права, или 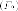 директриса;

• точки  называемыхвершинами эллипса.

Представление о форме эллипса дает следующее

Утверждение. Эллипс

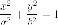
можно получить сжатием круга 

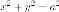
вдоль одной из двух взаимно перпендикулярных осей симметрии круга.

Доказательство. Направим вдоль пары взаимно перпендикулярных диаметров круга радиуса координатные ос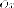ии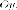Тогда уравнение окружности запишется в виде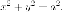

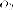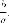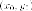Будем проводить сжатия вдоль оси с коэффициентомПусть точка с координатамипринадлежит кругу, то есть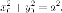Тогда точка с координатамипринадлежит эллипсу. Действительно,

Замечания.

1. Эксцентриситет 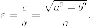Чем ближе значение эксцентриситета к нулю, тем ближе форма эллипса к кругу. При 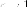форма эллипса приближается к отрезку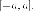

2. Если фокусы эллипса расположены на оси 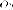симметрично относительно начала координат, то уравнение эллипса имеет канонический вид, но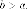есть- большая полуось, - малая полуось. Тогда величина фокусы имеют координаты эксцентриситет уравнения директрис  

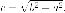
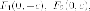
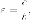
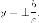
Пример. Установить, что уравнение 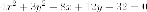задает эллипс, найти все его параметры.

Выделяем полные квадраты

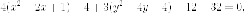
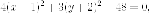
Итак, большая полуось малая полуось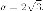

Центр имеет координаты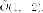 

Величина 

Эксцентриситет 

Фокусы находятся на оси симметрии на расстоянииот центра эллипса, то есть в точках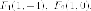

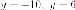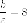Директрисы имеют уравнения (на расстоянииот центра).

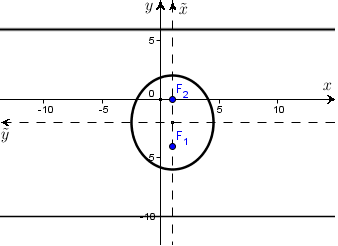
Каноническое уравнение этого эллипса

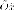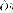Каноническая система координат: ось совпадает с, осьсовпадает с.

Фокусное свойство эллипса

Отрезок, соединяющий фокус с точкой на эллипсе называется фокальным радиусом этой точки.

Утверждение. Пусть фокальный радиус с левого фокус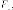аафокальный радиус с правого фокуса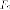к одной и той же точки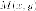на эллипсе. Тогда

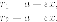
Доказательство. Действительно, Следовательно точк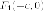ии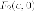находятся внутри эллипса. С уравнение эллипса находим, что 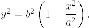Пусть - точка на эллипсе с координатами тогда вычислим расстояние от этой точки до левого фокуса: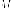

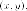
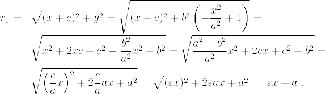
Но так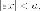откудаесть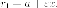

Аналогично проверяется, что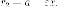  

Как следствие получаем фокусное свойство эллипса.

Для любой точки на эллипсе

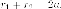
Фокусное свойство полностью Характеризуя эллипс.

Упражнение. Доказать, что геометрическое место точек, сумма расстояний от которых до двух различных заданных точек равна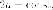является эллипс с фокусамии большой полуосью

Утверждение. Размер равна половине длины фокальной хорды, перпендикулярной фокальной оси.

Доказательство. Действительно,