Цилиндры.

Если в качестве направляющей цилиндрической поверхности выбрать любую из 9 кривых второго порядка, а образующие направить перпендикулярно плоскости, в которой эти кривые лежат, то такая цилиндрическая поверхность будет задаваться многочленом 2-го порядка, то есть будет поверхностью второго порядка в пространстве.

Направим ось декартовой прямоугольной системы координат перпендикулярно плоскости кривой 2-го порядка, а ос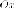ии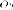совместим с осями канонической системы координат для соответствующей кривой. При таком выборе координатной системы уравнения 9 типов кривых второго порядка зададут 9 типов цилиндров второго порядка.

Эллиптический цилиндр (действительный)

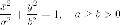
Эллиптический цилиндр имеет

• две фиксированные плоскости симметрии  - плоскост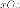и и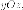и семьюплоскостей симметрии, которые перпендикулярны образующим;

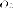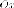• одну фиксированную ось симметрии  - ось i  семью осей симметрии, параллельные осями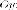

• линию центров симметрии, которые лежат на оси 

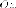
Воображаемый эллиптический цилиндр

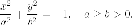
Гиперболический цилиндр

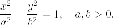
Гиперболический цилиндр имеет

• две фиксированные плоскости симметрии  - плоскост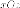и и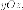i  семьюплоскостей симметрии, которые перпендикулярны образующим;

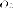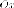• одну фиксированную ось симметрии  - ось и  семью осей симметрии, параллельные осями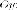

• линию центров симметрии, которые лежат на оси 

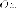
Параболический цилиндр

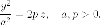
Параболический цилиндр имеет

• одну фиксированную плоскость симметрии  - плоскость 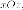i  семью плоскостей симметрии, которые перпендикулярны образующим;

• семью  осей симметрии, параллельные оси

• ни центра симметрии.

Цилиндры, которые построены над парами прямых, является парами плоскостей, они образуют класс поверхностей второго порядка, которые распадаются .

Пара действительных плоскостей, пересекающихся

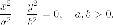
Пара мнимых плоскостей, пересекающихся

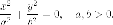
Пара действительных параллельных плоскостей

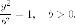
Пара мнимых параллельных плоскостей

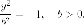
Пара плоскостей, совпадают

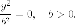
Сущность классификационной теоремы состоит в том, что выбором подходящей декартовой прямоугольной системы координат уравнения любой поверхности 2-го порядка может быть сведена к одному из перечисленных 17 типов уравнений 2-го порядка. Тем самым, любая поверхность 2-го порядка является одной из перечисленных 17 поверхностей. Это два эллипсоиды, два гиперболоиды, два параболоиды, два конуса, четыре цилиндра, не распадаются, и пять цилиндров, распадаются.

Прямолинейные образующие. Касательная плоскость

При изучении сечений поверхностей второго порядка, можно было заметить, что в некоторых случаях, а именно в случае однополостного гиперболоида и гиперболического параболоида, существовали плоскости, пересекающие эти поверхности по паре прямых, которые пересекаются. Оказывается, что эти две поверхности обладают той замечательным свойством, что они могут быть образованы из двух семей прямых, которые пересекаются.

Прямолинейные образующие на поверхности однополостного гиперболоида

Уравнение однополостного гиперболоида имеет вид:

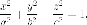
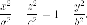
Разложим на множители:

Рассмотрим следующую систему линейных уравнений:

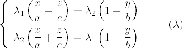
Каждое линейное уравнение задает в пространстве плоскость. Данные плоскости не параллельны, следовательно эта система из двух линейных уравнений задает прямую. Покажем, что эта прямая лежит на Однополостный гиперболоид. Действительно, если точка принадлежит этой прямой, то она удовлетворяет каждое из линейных уравнений системы, следовательно удовлетворяет произведения этих уравнений, то есть уравнению однополостного гиперболоида.

Это утверждение справедливо для любых 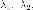которые не равны нулю одновременно. Итак, мы получилиуравнение одной  семьи прямолинейных образующих на Однополостный гиперболоид.

Уравнение второй семьи :

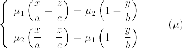
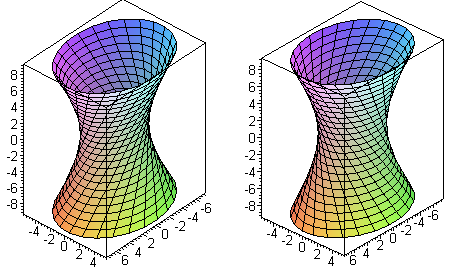
Теорема. Однополостный гиперболоид несет на себе две  семьи прямолинейных образующих, имеющих следующие свойства:

• через любую точку проходит ровно одна прямая с каждой семьи ;

• любые две образующие из разных семей лежат в одной плоскости;

• любые две образующие с одной  семьи является скрещивающимися;

• любые три образующие с одной семьи не параллельны одной плоскости.

Доказательство можно посмотреть в методичке.

Пример. Найти прямолинейные образующие поверхности 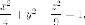которые проходят через точку

Запишем уравнение первой  семьи прямолинейных образующих 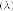и подставим координаты точки

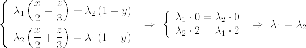
Можем взять любые числа, удовлетворяющие этому равенства, например: 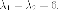Получаем уравнение прямолинейной образующей с первой семьи :

Уравнение второй  семьи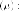 

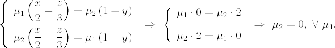
Возьмем, 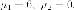получаем уравнение прямолинейной образующей с другойсемье :