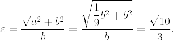Директориальна свойство эллипса

Утверждение. Для любой точки 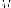на эллипсе

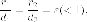
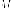где - расстояния от точкидо соответствующих директрис.

Доказательство. Действительно,

Тогда

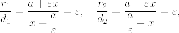
завершающий доказательства.

Директориальна свойство Характеризуя эллипс.

Упражнение. Пусть - фиксированная прямая, - фиксированная точка, не лежит на этой прямой. Геометрическое место точек на плоскости, отношение расстояний от которых до  расстояний от до есть величина постоянная является эллипс с эксцентриситетом , фокусом и директрисой

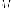
Пример. Написать уравнение эллипса, если известны его эксцентриситет 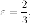фокус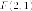и уравнение соответствующей директрисы

1 способ с использованием канонического уравнения.

Поскольку директриса перпендикулярна оси то оси эллипса параллельные осям координат, каноническая система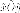 получается из данной параллельным переносом начала координат в центр эллипса. Поскольку 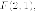то ось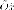совпадает сПусть центр эллипса находится в точке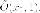

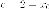 - расстояние от центра эллипса до фокуса; - расстояние от центра до директрисы. Итак, расстояние от фокуса до директрисы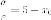

Поскольку 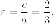тоНаходим

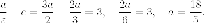
Итак 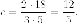Находим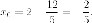Центр эллипса

находится в точке Находим

Каноническое уравнение эллипса:

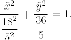
С учетом параллельного переноса отрумуемо общее уравнение эллипса:

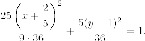
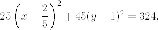
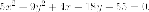
2 способ с использованием директориальнои свойства.

Отношение расстояния от произвольной точки 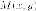эллипса до фокуса(в нашем случае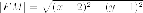) к расстоянию от точкидо соответствующей директрисы (в нашем случае) равна эксцентриситетаИтак

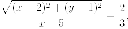
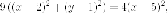
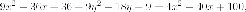
Выделением полных квадратов из этого уравнения можно получить каноническое.

Уравнение касательной к эллипсу

Утверждение. Если точка 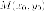лежит на эллипсе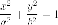, то уравнение касательной к эллипсу в этой точке имеет вид:

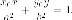
Доказательство . Пусть 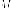лежит на верхней половине эллипса:

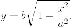
Вычислим 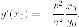Тогда для уравнения касательной последовательно находим:

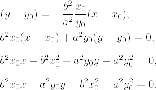
Разделим последнее равенство на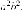 

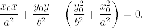
Итак,

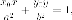
так как точка 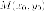 принадлежит эллипсу.

Упражнение. Докажите, что фокусы эллипса расположены по одну сторону от касательной в любой точке эллипса.

Оптическая свойство эллипса

Утверждение. Касательная к эллипсу образует одинаковые углы с локальными радиусами.

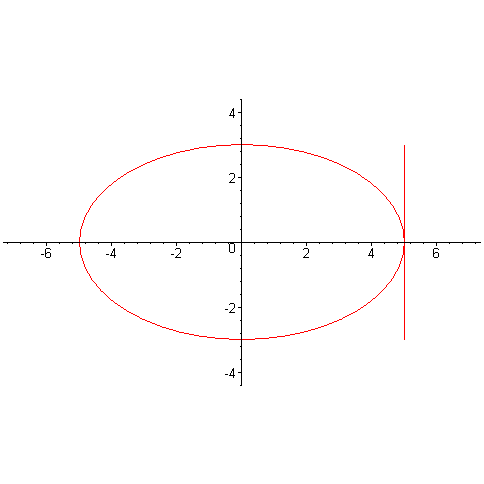
Доказательство. Пусть - касательная к эллипсу в точке с уравнением

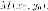
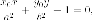
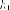- расстояние до касательной от левого 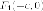фокуса и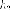- расстояние от правого 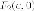фокуса. Тогда

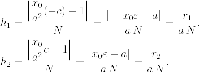
где - модуль вектора нормали касательной. Итак,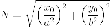

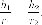
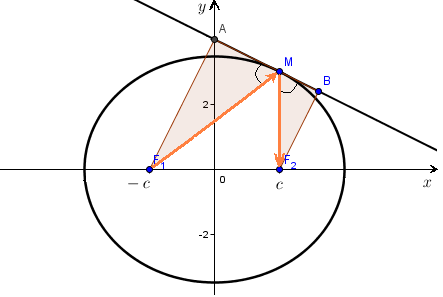
Последнее равенство означает равенство синусов углов, образованных локальными радиусами с касательной. Но так как оба угла острые, то из равенства синусов следует равенство самых углов.

Если представить эллипс как зеркальную кривую, то по законам оптики луч света, выпущенный с одной фокуса, после отражения от эллипса пройдет через второй фокус.

Источник: Файл:Ellipse with focus.svg - https://ru.wikipedia.org

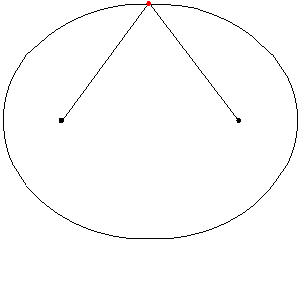
Источник: Файл:ElipseAnimada.gif - https://ru.wikipedia.org

шҐ˜ю~ э

Источник: Файл:Parametric ellipse.gif - https://ru.wikipedia.org

Гипербола.

ГМТ, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяют уравнению

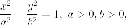
называется гиперболой . Данное уравнение называется каноническим уравнением гиперболы , а соответствующая система координат называется канонической . Если то гипербола называетсяравносторонний .

Следующие два утверждения дают представление о форме гиперболы.

Первое. Любая гипербола выходит из равносторонней путем сжатия (растяжения) плоскости вдоль оси 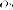с коэффициентом

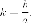
Действительно, пусть точка 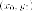принадлежит равностороннего гиперболе, то естьЛегко проверить, что в таком случае точка с координатами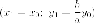принадлежит гиперболам

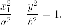
Второе. равностороннего гипербола 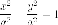получается поворотом на уголграфика обратной пропорциональной зависимости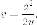

Пусть 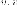декартовы координаты, и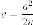график обратной пропорциональной зависимости. Осуществим вращения плоскости на угол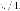Аналитическое задание такого преобразования

Итак, в новых координатах получаем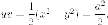 

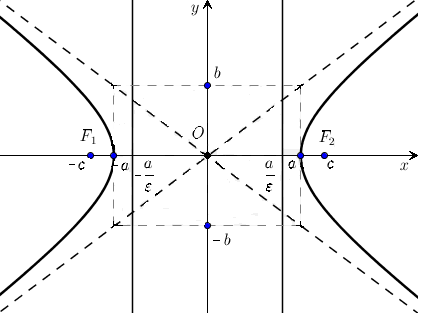
Геометрическими характеристиками гиперболы являются:

• две оси симметри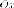и и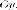одинцентр симметрии  - точка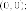

• параметр - действительно полуось , параметр  - мнимая полуось ;

• величина 

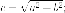
• точки 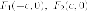называютсялевым и правым фокусами (очаговыми точками) } соответственно;

• величина - фокусное расстояние, то есть расстояние между фокусами;

• величина 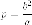– фокальный параметр;

• величина 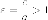– эксцентриситет;

• точки - вершины гиперболы (пересечение гиперболы с осью симметрии);

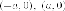
• две прямые - директрисы гиперболы;

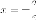
• две прямые - асимптоты гиперболы.

Замечания.

1. Эксцентриситет 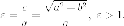Чем ближе значение эксцентриситета к единице, тем ближе форма гиперболы до двух луче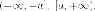йПри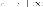форма гиперболы приближается к двум параллельных прямых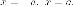

2. Гипербола с уравнением

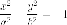
называется сопряженной к гиперболы с уравнением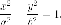

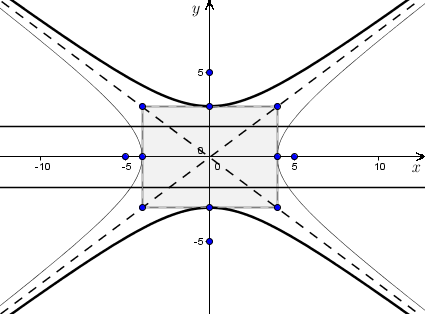
Для сопряженной гиперболы - действительно полуось, - мнимая пиввись. Вершины сопряженной гиперболы находятся в точках Размер имеет такое же значение фокусы сопряженной гиперболы расположены на оси и имеют координаты эксцентриситет уравнения директрис Асимптоты гиперболы и сопряженной гиперболы совпадают:

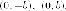
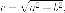
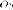
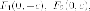
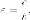
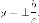
Пример. Вычислить эксцентриситет гиперболы, если ее асимптотами являются прямые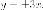 

Асимптоты имеют каноническое положение, следовательно гипербола имеет каноническое уравнение

Уравнения асимптот гиперболы 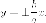Итак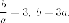

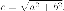Эксцентриситет где Итак

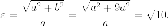
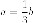Обычно в задачах подразумевается каноническая гипербола. Но мы можем рассмотреть все случаи. Сопряженная гипербола имеет такие же асимптоты, но Итак, имеем и