
- •Парабола.
- •Директориальна свойство параболы
- •Относился к притче.
- •Оптическая свойство параболы.
- •Фокусное свойство эллипса
- •Директориальна свойство эллипса
- •Уравнение касательной к эллипсу
- •Оптическая свойство эллипса
- •Фокусное свойство гиперболы
- •Директориальна свойство гиперболы
- •Уравнение касательной к гиперболе.
- •Оптическая свойство гиперболы.
- •Поверхности вращения
- •Поверхности переноса.
- •Цилиндры.
- •Прямолинейные образующие на поверхности однополостного гиперболоида
- •Прямолинейные образующие на поверхности гиперболического параболоида
- •Касательная плоскость
- •Свойства симметричной матрицы
- •Самосопряжённых оператор в евклидовом пространстве
- •Диагонализации квадратичной формы ортогональным преобразованием координат
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •Приведение общего уравнения поверхности второго порядка к каноническому виду
Фокусное свойство гиперболы
Отрезок, соединяющий фокус с точкой на гиперболе называется фокальным радиусом .
Утверждение. Пусть  фокальный
радиус с левого фокуса
фокальный
радиус с левого фокуса 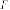 ,
а
,
а  фокальный
радиус с правого фокуса
фокальный
радиус с правого фокуса 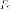 к
одной и той же точки
к
одной и той же точки 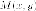 на гиперболе.
на гиперболе.
Тогда для точек левой ветви гиперболы
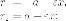
а для точек правой ветви
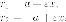
Доказательство. Пусть - расстояние от
точки на
гиперболе к левому фокуса. Вычислим
ее:
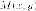
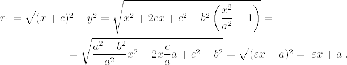
Аналогично находим
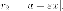
Рассмотрим правую ветвь. Для
точек правой ветви имеем 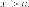 Так
как
Так
как 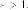 то
то 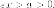 Значит
Значит 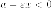 и
и 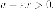 Раскрыв
модули, находим
Раскрыв
модули, находим
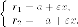
Рассмотрим левую ветвь. Для
точек левой ветви имеем 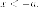 Так
как
Так
как 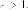 то
то  Следовательно
Следовательно 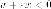 и
и 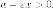 Раскрыв
модули, находим
Раскрыв
модули, находим
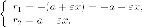
Как следствие получаем фокусное свойство гиперболы.
Для любой точки на гиперболе
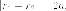
Доведння. Если
точка находится на правой ветке,
то 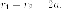 Если
же точка на левой ветке,
тогда
Если
же точка на левой ветке,
тогда 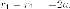 Значит
Значит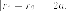
Фокусное свойство полностью Характеризуя гиперболу.
Упражнение. Доказать,
что геометрическое место точек, разность
расстояний от которых до двух
различных заданных
точек  равна
равна 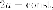 является
гиперболой с фокусами
является
гиперболой с фокусами  и
действительной полуосью
и
действительной полуосью
Директориальна свойство гиперболы
Утверждение. Для
биде точку 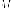 на
гиперболе
на
гиперболе

где - расстояния
от точки до
соответствующих директрис.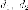
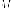
Доказательство. Рассмотрим правую ветвь, тогда
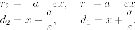
Итак,
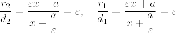
Для левой ветви доведите самостоятельно.
Директориальна свойство полностью Характеризуя гиперболу.
Упражнение. Пусть - фиксированная
прямая, - фиксированная
точка, не лежит на этой
прямой. 
 Геометрическое
место точек
Геометрическое
место точек 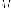 на
плоскости, отношение расстояний от
которых до
на
плоскости, отношение расстояний от
которых до  до
расстояний от
до
расстояний от 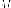 до
до  есть
величина постоянная
есть
величина постоянная 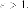 является
гиперболой с
эксцентриситетом
является
гиперболой с
эксцентриситетом  фокусом
фокусом  и
директрисой
и
директрисой
Уравнение касательной к гиперболе.
Утверждение. Если
точка 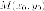 принадлежит
гиперболе, то уравнение касательной к
гиперболе в этой точке имеет вид:
принадлежит
гиперболе, то уравнение касательной к
гиперболе в этой точке имеет вид:
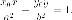
Доказательство аналогичное доказательству для касательной к эллипсу, проведите его самостоятельно.
Упражнение. Докажите, что фокусы гиперболы расположены по разные стороны от касательной в любой точке гиперболы.
Пример. С
точки  проведите
касаются гиперболы
проведите
касаются гиперболы
Точка  не
принадлежит гиперболе. Записываем
уравнение касательной к гиперболе в
неизвестной точке
не
принадлежит гиперболе. Записываем
уравнение касательной к гиперболе в
неизвестной точке 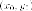 ,
принадлежащей гиперболе:
,
принадлежащей гиперболе:

Эта
касательная должна проходить через
точку  следовательно
следовательно

Поскольку
точка 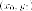 принадлежит
гиперболе, то
принадлежит
гиперболе, то 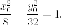 Итак,
Итак,
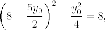
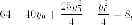

Есть
два корня этого уравнения 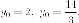 Итак,
имеем две точки
соприкосновения
Итак,
имеем две точки
соприкосновения 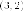 и
и 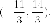 Уравнение
искомых касательных
Уравнение
искомых касательных
 и
и 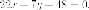
Оптическая свойство гиперболы.
Утверждение. Касательная к гиперболы образует равные углы с локальными радиусами.
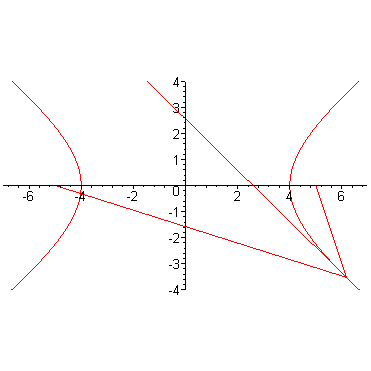 Доказательство. Пусть - касающаяся
гиперболы в
точке ее
уравнение
Доказательство. Пусть - касающаяся
гиперболы в
точке ее
уравнение 
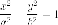
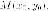
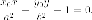
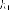 - расстояние до
касательной от левого
фокуса
- расстояние до
касательной от левого
фокуса 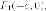 а
а 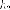 - расстояние до
касательной от правого
фокуса
- расстояние до
касательной от правого
фокуса 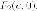 Вычислим
Вычислим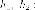
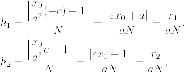
где - модуль
вектора нормали касательной. Очевидно,
что и
так как оба угла острые, то с равенства
синусов следует равенство самых
углов.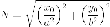
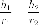
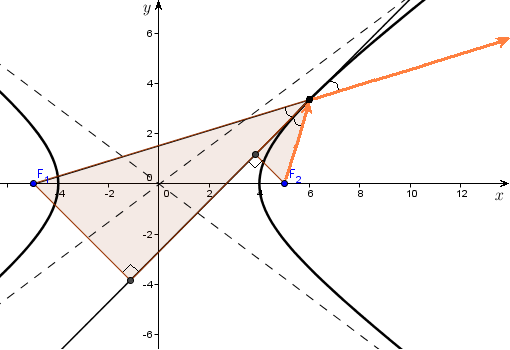
Если представить гиперболу как зеркальную кривую, то по законам оптики луч света, выпущенный с одной фокуса, после отражения от гиперболы идет так, будто его выпустили из второго фокуса.
Другие виды уравнений второго порядка.
Множество
точек 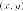 на
плоскости, удовлетворяющих
уравнению
на
плоскости, удовлетворяющих
уравнению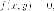 где-многочлен
второго порядка от двух переменных,
называется кривой второго порядка.
где-многочлен
второго порядка от двух переменных,
называется кривой второго порядка.
Эллипс, гипербола и парабола не исчерпывают весь класс кривых второго порядка. Рассмотрим другие виды уравнений и соответствующих кривых.
Воображаемый
эллипс.
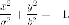
Эта «кривая» задает пустую множество точек на плоскости, но это множество задается многочленом 2-го порядка. Эта "кривая" имеет две "оси симметрии" и один "центр симметрии".
Пара
прямых, которые пересекаются.
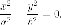
Действительно, разложение левой части на множители приводит к паре прямых
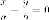 и
и 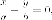
которые
пересекаются в точке 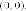 Эта «кривая» имеет две оси симметрии и
один центр симметрии.
Пара
мнимых прямых, которые пересекаются.
Эта «кривая» имеет две оси симметрии и
один центр симметрии.
Пара
мнимых прямых, которые пересекаются.
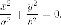
Единственной
точкой на плоскости, удовлетворяет
этому уравнению является точка 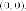 По аналогии с предыдущим уравнением,
говорят о паре мнимых прямых, пересекающихся
в действительной точке. Эта "кривая"
имеет две "оси симметрии" и "центр
симметрии".
По аналогии с предыдущим уравнением,
говорят о паре мнимых прямых, пересекающихся
в действительной точке. Эта "кривая"
имеет две "оси симметрии" и "центр
симметрии".
Пара
параллельных прямых.
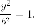
Это уравнение задает пару прямых
 и
и 
которые
очевидно параллельны. Эта «кривая»
имеет бесконечно много осей симметрии
(перпендикулярных этим прямым) и линию
центров симметрии – ось
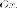
Пара параллельных воображаемых прямых.
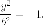
Это
уравнение задает пустую множество точек
на плоскости, но по аналогии с предыдущим
случаем эту "кривую" называют парой
параллельных воображаемых прямых. Эта
«кривая» имеет бесконечно много "осей
симметрии" и "линию центров
симметрии", - ось
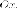
Пара прямых, совпадают.

Это
уравнение задает одну прямую - ось 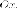 Но
так как эта прямая является предельной
для пары прямых
Но
так как эта прямая является предельной
для пары прямых при
при то
говорят о паре прямых, совпадают. Эта
кривая так же имеет бесконечно много
осей симметрии, перпендикулярных
оси
то
говорят о паре прямых, совпадают. Эта
кривая так же имеет бесконечно много
осей симметрии, перпендикулярных
оси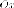 и
линию центров симметрии- ось
и
линию центров симметрии- ось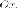
Классификационная теорема для кривых второго порядка.
Сущность классификационной теоремы состоит в том, что выбором прямоугольной декартовой системы координат уравнения любой кривой 2-го порядка может быть приведено к уравнению эллипса, гиперболы, параболы, воображаемого эллипса и перечисленным 5 типам уравнений пар прямых.
Эллипс (действительный и мнимый), гипербола и парабола образуют класс кривых 2-го порядка, которые не распадаются. Остальные кривых 2-го порядка - это кривые, которые распадаются (по парам прямых).
По количеству центров симметрии кривые 2-го порядка делят на центральные, имеющих единый центр симметрии, и нецентральные, не имеющих центра симметрии или имеющих более одного центра симметрии. К типу центральных относятся эллипсы (действительный и мнимый), гипербола, пары прямых, пересекающихся (действительных и мнимых). К нецентральных относятся парабола, пары параллельных прямых (действительных и мнимых) и пара прямых, совпадают.
Заметим, что в пересечении этих классов лежит парабола, она является единственной нецентральной кривой 2-го порядка, не распадается. Теорема . Пусть
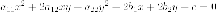
уравнение
кривой второго порядка. Тогда
существует декартова прямоугольная
система координат, в которой уравнение
данной кривой приводится к одному
из  типов:
типов:
