Аналитическая Геометрия.

Приведение общего уравнения кривой

второго порядка к каноническому виду

Общее уравнение кривой второго порядка имеет вид:

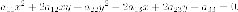
Квадратичная часть этого уравнения - это квадратичная форма

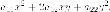
Матрица квадратичной формы:

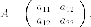
В каноническом уравнении матрица квадратичной части должно быть диагональной. Нам известно, что существует ортогональное преобразование координат такое, что матрица квадратичной формы в новых координатах имеет диагональный вид. Новый базис образуется из собственных векторов матрицы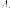

Итак, для того чтоб привести общее уравнение к каноническому виду нужно

• найти ортогональный базис из собственных векторов матрицы;

• перейти к новой системе координат, в которой матрица квадратичной части является диагональной;

• осуществить параллельный перенос начала координат таким образом, чтобы уравнение приняло канонический вид (например, в центр вершину кривой).

Пример. Привести к каноническому виду уравнение кривой

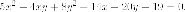
Найти каноническую систему координат.

Выписываем матрицу квадратичной части:

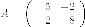
Характеристический многочлен этой матрицы:

Его корни, собственные числа матрицы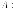 

Ищем собственные векторы.

Для собственный вектор находится из системы уравнений Матрица этой системы:

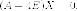
Итак, собственный вектор имеет направление 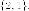Нормируем его (делим на длину) и берем в качестве первого нового базисного вектора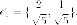 

Для собственный вектор находится из системы уравнений Матрица этой системы:

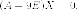
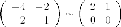
Итак, собственный вектор имеет направление Нормируем его (делим на длину) и берем в качестве второго нового базисного вектора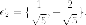 

Переходим к новой системе координат. Напомним, что старые координаты 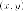связаны с новыми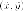следующим образом:

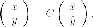
где - матрица перехода к новому базису, ее столбиками есть координаты новых базисных векторов в старом базисе.

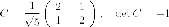
Матрица - ортогональная, ее определитель равен или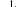В нашем случае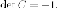есть при таком преобразовании координат мы изменим ориентацию плоскости, не желательно. Итак, для того чтобыориентация не изменилась, мы изменим направление нового второго базового вектора на противоположный, то есть возьмем 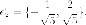Итак

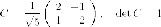
Преобразование координат

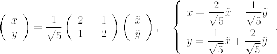
Подставляем эти выражения в уравнение кривой. В квадратичную часть подставлять не нужно, по известной теореме в базисе из собственных векторов матрица квадратичной части имеет диагональный вид, где диагонали стоят собственные числа. Нужно подставить эти выражения только в линейную часть:

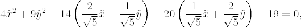
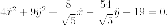
Выделяем полные квадраты:

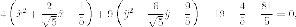
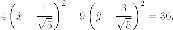
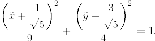
Делаем замену переменных, с геометрической точки зрения  - параллельный перенос:

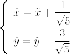
В новой системе координат имеем каноническое уравнение эллипса :

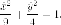
Теперь нужно выписать общее преобразование координат. Выражаем координаты 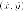через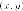

i подставляем в выражение для координат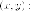 

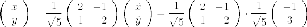
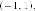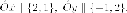Итак, это превращение дает нам каноническую систему координат: ее начало находится в точке с координатаминаправляющие векторы новых координатных осей(направляющий вектор - это не базовый вектор, он может быть не единичным).

Парабола.

Геометрическое место точек на плоскости, координаты которых в некоторой прямоугольной декартовой системе координат, удовлетворяющих уравнению

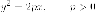
называется параболой. Это уравнение называется каноническим уравнением параболы, а соответствующая система координат называется канонической системой координат.

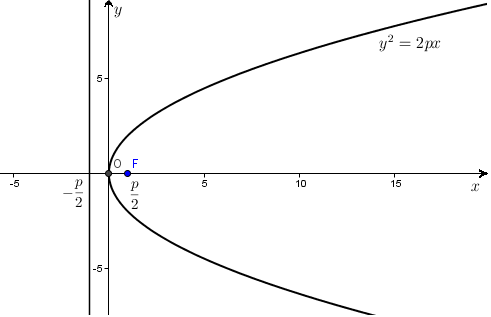
Геометрическими характеристиками параболы являются:

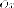•  - ось симметрии или фокусное ось ;

• параметр , который называется фокальным параметром ;

• точка - фокус параболы;

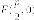
• прямая - директриса параболы.

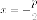
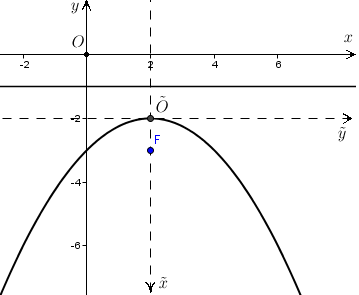
Пример. Установить, что уравнение 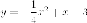задает параболу, найти все ее параметры.

Выделяем полный квадрат

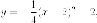 или 

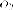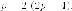Итак, ось симметрии параллельна оси , параметр равен Вершина имеет координаты 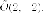Ветви параболы направлены вниз. Фокус находится на оси симметрии на расстоянии 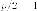вниз от вершины параболы, то есть в точке 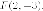Директриса имеет уравнение

Каноническое уравнение этой параболы Каноническая система координат: ось 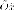совпадает с , которая направлена ​​вниз, ось 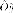совпадает с

Отрезок, соединяющий две точки параболы и происходит через фокус называется фокальной хордой .  Отрезок, который связывает фокус с любой точкой на параболе называется фокальным радиусом .

Утверждение. Для произвольной точки 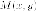на параболе ее фокальный радиус имеет вид:

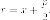
Доказательство. Пусть 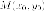принадлежит параболе. Тогда

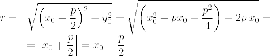
так як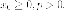 

Геометрический смысл фокального параметра проясняет

Утверждение. Фокальный параметр равен половине длины фокальной хорды, перпендикулярной фокальной оси.

Доказательство. Уравнение прямой, проходящей через фокус перпендикулярно фокальной оси: Итак, точки пересечения этой прямой с параболой:

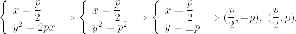
Длина соответствующей хорды: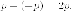 

Действительно, фокальный радиус точки на параболе, которая имеет ординату равна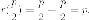

Директориальна свойство параболы

Утверждение. Пусть 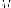- произвольная точка на параболе, - расстояние от точки до директрисы. Тогда d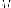  

Доказательство. Действительно,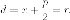 

Упражнение. Доказать, что справедливо обратное утверждение: геометрическое место точек, расстояния от которых до фиксированной точки и фиксированной прямой уровне, является параболой.

Пример. Написать уравнение параболы, если известны ее фокус 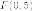и директриса

1 способ с использованием канонического уравнения.

Директриса перпендикулярна оси симметрии параболы, фокус находится на оси симметрии справа от директрисы. Итак ось симметрии параболы Каноническая система координат в данном случае получается параллельным переносом данной системы координат в вершину параболы.

Расстояние между фокусом и директрисой равна фокальному параметра Итак каноническое уравнение 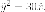Вершина находится посередине между фокусом и директрисой, следовательно имеет координаты 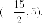Уравнение параболы:

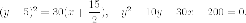
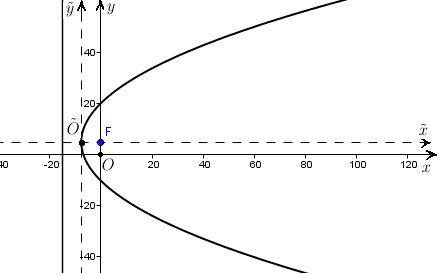
2 способ с использованием фокальной свойства.

Расстояния от произвольной точки 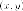на параболе до фокуса 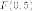и до директрисы уровне, то есть

Относился к притче.

Утверждение. Если точка 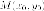принадлежит параболе, то уравнение касательной к параболе в этой точке имеет вид:

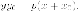
Доказательство. Действительно, рассмотрим точки параболы в полуплоскости 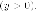Тогда 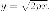Поскольку уравнение касательной для явно заданной кривой имеет вид  а 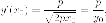 то имеем

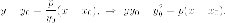
Поскольку 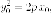получаем 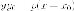- уравнение касательной.

Пример. Написать уравнение касательной к параболе параллельной прямой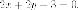

Решать эту задачу можно двумя способами.

1 способ. Записываем уравнение касательной к параболе в неизвестной точке 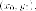принадлежащей параболе:

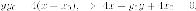
Эта касательная должна быть параллельна прямой 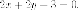Условие параллельности двух прямых:

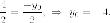
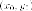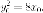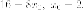Поскольку точка принадлежит параболе, то Итак, Уравнение искомой касательно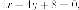й или

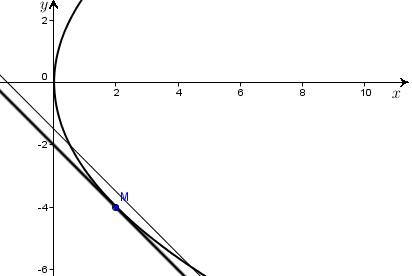
2 способ. Записываем уравнение прямой, параллельной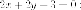 

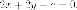
Ищем точки пересечения прямой и параболы

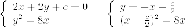
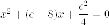
Касательная имеет с кривой единую двойной точку пересечения, то есть дискриминант должен равняться нулю. Итак 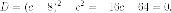Отсюда Точку соприкосновения ищем при 

Итак уравнение касательно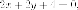й или