Элементы-алгебры-Шайкин-А.Н

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский химико-технологический университет им. Д.И. Менделеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

второй – B

. Легко проверить, что первая квадратичная форма

..pdf

Скачиваний:

697

Добавлен:

12.03.2016

Размер:

1.95 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1212

1	0	1	0

S 1 1	1	0	0	.
1	1	1	0
	1	1	1
2	1	1	1
	1		0 1		0 2 2				2		1 1 1			1	0	1	0	0	0

																	1	0	0
Тогда B		1	1 0		0	3	3		2		1	1 0		1	0	0	1	0	0	.
Тогда B		1	1 0		0	3	3		2		1	1 0		1	0	0		2	1	.
	1		1 1 0 3 2						3		1 0 1			1	0	0 0		2	1
																		0	2
		2	1 1 1			2 1			1		2	1 1		0	1	0 0		0	2
		2	1 1 1			2 1			1		2	1 1		0	1	0 0
Пример 3. Составить матрицу A квадратичной формы от трех
неизвестных f (x , x , x ) 7x2						3x2	4x x			2	x	2	x .
		1	2	3	1	3		1		2		2	3

Решение. Матрица этой квадратичной формы имеет вид:

				7			2	0
			A		2		0
			A		2		0	0,5 .
					0	0,5		3
					0	0,5		3
Пример 4. Указать квадратичную форму f, соответствующую
симметрической матрице						4	1	1
						4	1	1
						1	5	3
				A		1	5	3	.
						1	3	2
						1	3	2
Является ли указанная квадратичная форма невырожденной?
Решение. Порядок матрицы A равен трем, поэтому квадратичная форма f
будет зависеть от трех неизвестных. Тогда
f (x , x , x ) 4x2 5x						2 2x2		2x x			2		2x x 6x				x .
1	2	3	1			2	3		1		2		1	3		2		3
Вычислим определитель:			\| A\| 40 3 3 5 2 36 79.												Поскольку \| A\| 0,
то квадратичная форма f невырождена.
Пример 5. Дана квадратичная форма
f (x , x , x ) x2				2x2 5x2 2x x						2		2x x 6x			2		x .
1	2	3	1		2		3	1		2			1	3	2			3

Привести эту форму к каноническому виду с помощью перехода к другому базису.

Решение. Выделим вначале полный квадрат по переменной x1, получим:

f(x12 2x1x2 2x1x3) 2x22 5x32 6x2x3

((x1 x2 x3)2 x22 x32 2x2x3) 2x22 5x32 6x2x3

(x x x )2 3x2						4x2			8x x .
1		2	3		2		3			2	3
Далее, выделим полные квадраты по переменным x2										и x3 :
f (x x		x )2		3	x2		8	x x		4x2
f (x x	2	x )2		3	x2			x x		4x2
1	2		3		2		3		2 3		3
							3

111

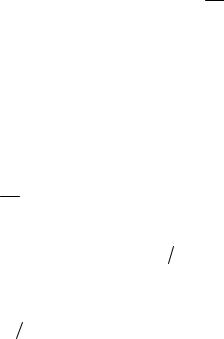
(x x	x		2		x	4	x	2	16	x	2	4x	2
		)		3
		)		3
1 2	3				2	3	3		9	3		3
						3			9

(x x		x )2	3	x		4	x	2	16	x2	4x2
	2				2
1		3				3	3		3	3	3

(x x x )2	3	x				4	x		2	28	x2 .
(x x x )2	3	x					x				x2 .
1 2 3			2		3			3		3	3
Положим					3					3
Положим
y1 x1 x2 x3 ,
			4
			4
y2	x2			x3	,
y2	x2		3	x3	,
	x .		3
y	x .
3	3

Тогда квадратичная форма f примет канонический вид:

g(y1, y2, y3) y12 3y22 28 y32 .

Покажем, что y1,y2,y3 – базис. В матричном виде замена переменных

y1 x1 x2 x3 ,

				4
				4
	y2		x2		x3	,
	y2		x2	3	x3	,
			x ,	3
	y		x ,
		3	3			f
приводящая	квадратичную	форму				f	к	каноническому	виду

g(y1, y2, y3) y12 3y22 28 y32 , выглядит следующим образом:

							y1			1		1	1	x1
							y		2		0	1	4 3	x	.
									2		0	0	1	2
							y				0	0	1	x
									3					3
		1		1	1
Матрица S	1		0	1	4	3		имеет ненулевой определитель. Поэтому и матрица
Матрица S			0	1	4	3		имеет ненулевой определитель. Поэтому и матрица
			0	0	1
			0	0	1

S (столбцами которой являются координаты в старом базисе векторов нового базиса) также невырождена. Заметим, что ранг исходной квадратичной формы f равен 3, так как число ненулевых коэффициентов в каноническом виде равно 3.

Пример 6. Привести квадратичную форму f (x ,x		) 2x2	5x	2	4x x	2	к
1	2	1		2	1	2

каноническому виду двумя способами: с помощью ортогонального преобразования (записать явный вид этого преобразования) и методом Лагранжа. Проверить выполнение закона инерции.

Решение. 1-й способ. Матрица квадратичной формы имеет вид:

2		2	. Собственные значения:
A			. Собственные значения:
	2	5
	2	5

112

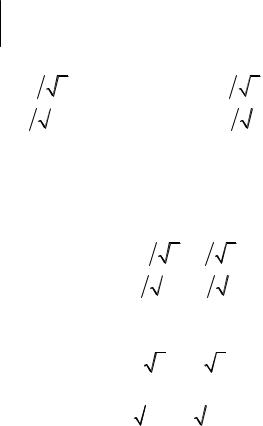
2	2	0	2 7 6 0	1,
2	5
				6.

Тогда ортонормированный базис собственных векторов:

	2		5		1		5		6).
e				(для 1); e				(для	6).
1		1	5	2		2	5
		1	5			2	5

Векторы e1 и e2 (в силу того, что матрица A – симметрическая, собственные числа различны) взаимно-ортогональны. Впрочем, условие ортогональности e1 и e2 можно проверить и непосредственно, так как скалярное произведение e1 e2 0. Отсюда, матрица S ортогонального преобразования имеет вид:

2		5	1	5
S					.
	1	5	2	5

Тогда явный вид этого ортогонального преобразования следующий:


x				2			y	1		y			,
x							y			y		2	,
	1	5				1		5				2
		5						5
			1					2
x			1		y			2	y	2	.


2		5				1		5
		5						5

С помощью этого преобразования квадратичная форма f примет вид:

									g(y ,y				) y2		6y2 .
											1	2		1			2
2-й способ. Выделим полные квадраты по переменным x1 и x2 :
		f (x ,x		2	) 2(x2	2x x		2	) 5x	2	2((x			x	2	)2	x2) 5x	2	2(x	x	2	)2 3x	2 .
		1		2	1		1	2		2			1		2		2	2	1	f	2		2
Положим			z1 x1 x2,				z2	x2 .			Тогда			квадратичная					форма	f		примет вид:
h(z ,z	2	) 2z2			3z2 .
1	2		1		2

Закон инерции, очевидно, выполняется.

Пример 7. Является ли положительно определенной квадратичная форма

f (x1, x2, x3) 5x12 x22 4x32 4x1x2 2x1x3 2x2x3 ?

							5	2	1
	Решение. Матрица квадратичной формы имеет вид:							1
	Решение. Матрица квадратичной формы имеет вид:						A 2	1	1 .
								1
							1	1	4
Тогда	1 5 0,	2	5	2	1 0,	3 det(A) 20 2 2 1 16 5 2 0.
			5	2
			2	1

Значит, по критерию Сильвестра, квадратичная форма f (x1, x2, x3) является положительно определенной.

Пример 8. Привести к каноническому виду одновременно две квадратичные формы

45x12 72x1x2 18x1x3 45x22 18x2x3 18x32 ,

113

90x2	144x x		2	36x x			106x2	36x		x 36x2 .
1		1	2		1	3	2		2	3	3	45		36	9
												45		36	9
Решение. Матрица		первой			квадратичной				формы		A		36	45	9	, а
Решение. Матрица		первой			квадратичной				формы		A		36	45	9	, а
													9	9	18
													9	9	18

положительно определенная. Приведем ее к каноническому виду, выделяя полные квадраты.45x12 72x1x2 18x1x3 45x22 18x2x3 18x32

36x12 72x1x2 36x22 9x12 18x1x3 9x32 9x22 18x2x3 9x32

(6x1 6x2)2 (3x1 3x3)2 (3x2 3x3)2 (x1)2 (x2)2 (x3)2 ,

6x1 6x2

3x2 3x3.

где

Так

как

то

x2 3x1 3x3

1/12

1/ 6

1/6

S 1

Тогда

1/12

1/ 6

Следовательно,

1/ 6

1/12

1 0

19/9

2/9

C S T

, а

D ST BS

2/9

22/9

4/9

Теперь

найдем

0 0

2/9

4/9 22/9

характеристический

многочлен

матрицы

19/9

2/9

22/9

4/9

2/9

4/9

22/9

3 7 2

16 12,

его корни

Собственные

векторы,

2,3

соответствующие

3, имеют вид

. Тогда в качестве базисного

1/3

можно

взять

(нормированный)

h 2/3 .

Собственные

векторы,

2/3

2C1 2C2

соответствующие

имеют

вид

Легко проверить, что

2,3

каждый из них ортогонален h1 .

Выберем два,

ортогональных между собой.

114

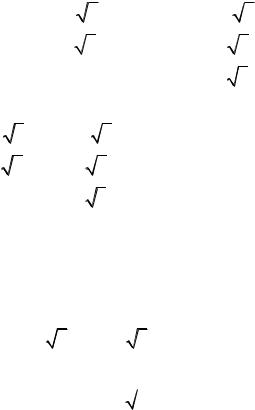
				2					2			2C1 2C2
Пусть					1	. Тогда	h	найдем из равенства		1			C	0, т.е.
Пусть	h				1	. Тогда	h	найдем из равенства		1			C	0, т.е.
		2					3						1
					0					0			C2
					0					0			C2
											2
4C 4C												4	. Нормировав h
4C 4C		2	C 0. Значит, в качестве h можно взять h									4	. Нормировав h
1		2		1				3	3					2
												5
												5

								2/		5					2/ (3 5)
и h3 ,																				h1 ,	h2		h3
и h3 ,	получим					h2 1/				5			и	h3 4/ (3			5) .	Записывая		h1 ,	h2	и	h3		как
									0

															5/(3	5)

столбцы			матрицы,						получим						матрицу		ортогонального			преобразования
1/3 2/								2/ (3												1 0			0
1/3 2/							5	2/ (3				5)								1 0			0
																		T	CS2
S2 2/3				1/		5		4/ (3			5) .				Следовательно,			T			0	1	0	,	а
S2 2/3				1/		5		4/ (3			5) .				Следовательно,			E S2			0	1	0	,	а
																					0 0		1
	2/3				0			5/(3 5)
	2/3				0			5/(3 5)
				3		0		0
				3		0		0
F S2	T	DS2			0	2		0
F S2		DS2			0	2		0	. Тогда преобразование, приводящее к каноническому
					0	0		2
					0	0		2

виду одновременно две данные квадратичные формы, будет иметь матрицу

7/36		5 /15				5 / 45
	1/ 4		0			0			сами		квадратичные формы будут
S S1 S2	1/ 4		0			0		, а	сами		квадратичные формы будут

	1/36		0			5 /9
	1/36		0			5 /9
		2		2			2		2			2		2	.
приведены к виду (x1)			(x2)		(x3)			и 3(x1)		2(x2)			2(x3)		.

5.10. Задачи для самостоятельного решения

Задача 1. Доказать, что e –										базис. Найти координаты x в этом базисе,
если они даны в стандартном:
	1			1						0		;
а) e e1,e2 , e1	, e2				1	,		x				;
	1				1					1
б) e e ,e ,e , e		1		, e		1			, e		0		, x	1
б) e e ,e ,e , e			1	, e			0		, e			1	, x	1	;
1 2 3	1			2					3
			0				1					1
			0				1					1		1

115

						, e		1			, e				1						, e					1		, x					0
в) e e ,e ,e						, e			0		, e						1				, e					1		, x						0		;
		1 2 3				1						2										3
									0								0																	1
									0								0									1								1
										1								0									0										0						1
г) e e ,e ,e ,e ,										1		,								2								1									1							1
г) e e ,e ,e ,e ,							e					,	e									, e							,		e								,	x					.
		1 2 3 4						1		1				2				0					3				3					4					0						4
																				0								1
										1										0								1									4						2
	Задача 2. Найти координаты вектора																															x			в базисе										если они даны в
	Задача 2. Найти координаты вектора																															x			в базисе								e ,		если они даны в
базисе e:
	1 0								1 1															0
а) e			0	,		; e		,							1		; x							;
			0	1					1						1									1
	1 1 0											0 0 4																			1
б) e														0						3			0												;
б) e	1			, 0 , 1			; e							0		,				3		,	0		;			x			1				;
														2						0			0
			0 1			1								2						0			0								1
	1 1 1											1 0 3																		0
в) e			0																2													0			;
в) e			0	, 0 , 1 ;					e			1 ,							2		, 1			;				x				0			;
			0																0													1
			0	1		1						1							0		0											1
	2 3 0 4																3 3 3 3																							1
			0						0											0											0										1
			0		4 0				0											0		1			1						0										1
															0 , 2 , 2 , 2 ; x 4
г) e 4 , 2 , 1 , 3 ; e															0 , 2 , 2 , 2 ; x 4

			0						3											0			4								0										2
			0		4 0				3											0			4		0						0										2
	Задача 3. Ортонормировать базис e:
	3 2																												1 1 0
	3 2																						б) e														0
а) e				,	3	;																	б) e						1					,			0		, 1		;
	1				3																										0
																															0		1					1
	1 0 3																												2 3 0 4
	1 0 3																														0						4			0			0
в) e	1 ,				2	, 1	;																г) e								0		,				4	,		0	,		0	.
					0																								4 2 1 3
	1				0	0
																															0 4 0										3
																															0 4 0										3
																																										, если она дана в базисе
	Задача 4. Найти матрицу оператора A в базисе e																																									, если она дана в базисе

116


	1 0					1 1									1		2	;
а) e		0	,	; e	,			1	; A
			1			1									3		4
	1 1 0						0 0 4											1 1			0
б) e								0			3			0		;				0 1	0		;
	1		, 0	, 1		; e			,				,				A
		0						2			0			0						0 0	2
			1	1
	1 1 1						1 0 3											1 1			0
в) e		0								2							A		0 1		1
			, 0	, 1 ; e			1 ,					, 1			;							;
		0								0									0 0		1
			1	1			1					0

1 1 0 1						1 1 1 1					1		0 0	0
	0		0				0			0		0	2 0	0
		1		0				1	1
											; A 0		0 3	0
г) e 1 , 1 , 1 , 1 ; e					0 , 1 , 1 , 1

	0		0				0			0		0	0 0	4
		1		1				0	1

Задача 5. Найти собственные значения и собственные (и присоединенные) векторы оператора, заданного матрицей:

2		1	;	2		1	;	3		1	;
а)	1	4		б)	3	4		в)	4
										1

1		1
г)	2	3	.

Задача 6. Найти матрицу оператора в базисе из собственных и присоединенных векторов, если она дана в стандартном базисе:

	0		1	0			12	6	2		4		5	2			1		3	3
а)		4	4	0	;	б)		9	3	; в)		5	7	3	;	г)		2	6	13
							18														.
		2	1	2				9	3			6	9	4				1	4	8
							18

Задача 7. Привести к нормальному виду методом выделения полных квадратов:

а)x2	x2	3x2		4x x 2x x 2x						x ;
1	2		3	1	2		1	3	2	3
б)x2	2x2		x2	2x x		2	4x x 2x x ;
1		2	3	1		2	1	3	2	3

в)x12 3x32 2x1x2 2x1x3 6x2x3;

г)x1x2 x1x3 x1x4 x2x3 x2x4 x3x4 .

Задача 8. Привести к каноническому виду методом ортогонального преобразования, найдя собственные векторы матрицы квадратичной формы:

а)3x2	3x2		4x x 4x x 2x x ;
2		3	1	2	1	3		2	3
б)7x2	7x2		7x2	2x x 2x x 2x x ;
1		2	3		1	2	1	3	2	3
в)x2 2x x 2x x 2x x ;
1	1	2	1	3	2		3
г) 3x2	3x2		x2 6x x 4x x .
1		2	3	1	3		2	3

Задача 9. Проверить квадратичные формы на знакоопределенность:

а)3x12 3x22 3x32 2x1x2 ;

117

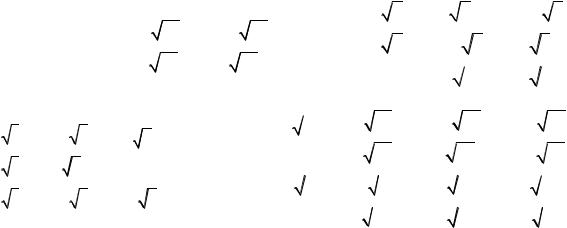
б)5x12 3x22 4x32 4x1x3 4x2x3 ; в)27x12 3x22 10x1x2 ;

г) 2x12 4x22 3x32 4x1x2 2x1x3 .

Задача 10. Привести к каноническому виду одновременно две квадратичные формы и найти матрицу данного преобразования:

а)45x2		72x x			2	18x x				45x2	72x	x		153x		2	,
	1	1			2		1	3		2	2	3			3
90x2	144x x			2	36x x				106x2		192x x				342x2			;
1		1		2		1	3			2		2	3				3
б)45x2		72x x 18x x 45x2									54x	x 90x2				,
	1	1			2		1		3	2	2	3			3
90x2	144x x			2	36x x				106x2		140x x				196x2			;
1		1		2		1	3			2		2	3				3
в)45x2		72x x 18x x 45x2									36x	x 45x2				,
	1	1			2		1		3	2	2	3			3
90x2	144x x			2	36x x				106x2		88x x			94x2		;
1		1		2		1	3			2	2	3			3
г)45x2		72x x 18x x 45x2									18x x 18x2 ,
	1	1		2		1		3		2	2	3			3
81x2	132x x				54x x				102x2		48x x			27x2 .
1		1	2			1	3			2	2	3			3

5.11. Ответы

	1/ 2		1/ 2		0
1. а)	1/ 2	; б)		; в)		; г)
1. а)		; б)	1/ 2	; в)	1	; г)
	1/ 2				1
			1/ 2		1

11 . 2.

1/ 2 а) ; б)

1/ 2

1			1
	2/3	; в)		0	;
	2/3	; в)		0	;
				0
1/ 2				0

	3										1/			1/				1/
	3										1/		2	1/		6		1/		3
	5/ 2		3/			1/
					10				10
г)		. 3. а)			10				10
г)		. 3. а)				,				; б)	1/		2 , 1/				6 , 1/		3		;
3/ 2			1/	10			3/	10				0
3/ 2			1/	10			3/	10
	4														2/	6			3
	4														2/	6		1/	3


													1/					5	2/					55 4/							22 2/									66

1/ 3 1/ 6 1/ 2


																	0				5/			55 1/					22 5/											66
																	0				5/			55 1/					22 5/											66
в) 1/		3 , 2/				6 , 0			;			г)								,							,						,								.
в) 1/		3 , 2/				6 , 0			;			г)								,							,						,								.
															2/ 5					1/					55 2/					22 1/								66
															2/ 5					1/					55 2/					22 1/								66

1/ 3				1/ 6				1/ 2									0
1/ 3				1/ 6				1/ 2															22					5/	55						6/
																					1/		22					5/	55						6/				66
			5		1				3/ 2			3/ 4					1										2							2						1
4.	а)		5		1		;	б)		2/3			1				0				;		в)														1/3					;
4.	а)			2			;	б)		2/3			1				0				;		в)				1/ 2 1/3										1/3					;
				2	0					1/ 4		3/8																0				2/3					2/3
										1/ 4		3/8				3/ 2												0				2/3					2/3
3		0		0		0
	0 4 0				0						3,			1								0	; б) 1,											1		,		5,
г)							. 5. а)				3,	h				, h							; б) 1,						h							,		5,
0		2 2				0			1,2			1					2									1			1								1
0		2 2				0								1								1												1
	2	3		0	1
	2	3		0	1

118

		1				;			в)									1,2			1,													1											0				;			г)					1,2		2 i,											1
h2						;			в)									1,2			1,										h1				2		,		h1										;			г)					1,2		2 i,						h1,2							.
		3																																	2										1																									1 i
		2						0 0																							0			0 0																1 0								0								1					1 0
6. а)			0					2 1									;				б)												0	0 1				;							в)							0 0						1	;			г)					0			1 1
6. а)			0					2 1									;				б)												0	0 1				;							в)							0 0						1	;			г)					0			1 1		.
			0					0 2																									0	0 0																		0 0						0									0			0 1
			0					0 2																									0	0 0																		0 0						0									0			0 1
							2									2								2			;																2						2						2	;													2			2	;
7. а) (x1)								(x2)										(x3)									;										б) (x1)								(x2)						(x3)					;								в) (x1)						(x2)			;
			2									2								2											2	.																														2						2				2	;
г) (x1)				(x2)											(x3)							(x4)										.																						8. а) 4(x1)									4(x2)						2(x3)				;
					2												2											2		;																														2						2						2	;
					2												2											2																																2						2						2
б) 6(x1)							6(x2)											9(x3)																																				в) (x1)							3(x2)						3(x2)
				2			(1																		2														2	.						9. а) положительно																			определена;
				2																					2														2
г) 3(x1)																17)(x2)													(1 17)(x2)
б) положительно																			определена;																	в) положительно																определена;											г) отрицательно
определена.																																				2						2					2	,														2						2				2	,
определена.																											10. а) (x1)										(x2)							(x3)				,											3(x1)				2(x2)						2(x3)				,
19/90													/15						2										/ 45
19/90										5			/15						2						5				/ 45
																																												2					2						2							2						2				2
	4/15											0													5 /15 ;										б)									2					2						2	,						2						2				2	,
	4/15											0													5 /15 ;										б)			(x1)							(x2)						(x3)					,			3(x1)				2(x2)						2(x3)				,
	1/90											0								2

																									5 / 45

5/ 24												/15														/30
5/ 24									5			/15										5				/30
																																									2						2						2									2						2				2
19/72								0															5 /18 ;																		2						2						2	,								2						2				2	,
19/72								0															5 /18 ;													в) (x1)								(x2)					(x3)					,					3(x1)				2(x2)						2(x3)				,

								0													5 /18
1/ 72								0													5 /18

11/54														/15						2										/135
11/54											5			/15						2						5				/135
																																													2						2						2						2						2			2
7/ 27												0								5 / 27 ;																	г)								2						2						2	,					2						2			2	,
7/ 27												0								5 / 27 ;																	г)			(x1)						(x2)						(x3)						,		2(x1)				3(x2)						(x3)			,
	1/54											0								2

																											5 / 27

1/9				7/36													1/9
	0					1/ 4												0
	0					1/ 4												0				.
				1/36														2/9
1/9				1/36														2/9

119

Учебное издание

ШАЙКИН Александр Николаевич

ЭЛЕМЕНТЫ АЛГЕБРЫ

Редактор: Е. В. Копасова

Подписано в печать 16.12.13 г. Формат 60×84 1/16. Усл. печ. л. 7,0. Уч.-изд. л. 8,7. Тираж 1000 экз. Заказ

Российский химико-технологический университет имени Д. И. Менделеева Издательский центр

Адрес университета и издательского центра: 125047, Москва, Миусская пл., 9

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1212

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.09.20194.78 Mб6Экзаменационный билет N 19.doc
#
13.02.2015125.44 Кб25Экология курсовая.doc
#
13.02.201529 Кб18экология.docx
#
13.02.2015133.04 Кб13ЭКОНОМ ЗАЧЕТ.docx
#
15.04.2019591.87 Кб2экономика_7 задание.doc
#
12.03.20161.95 Mб697Элементы-алгебры-Шайкин-А.Н..pdf
#
01.03.202567.89 Кб3ЭМП.docx
#
23.11.2019144.38 Кб85Эпоксидные смолы.doc
#
13.02.201513.76 Mб59Эффект Комптона.doc
#
26.11.201965.02 Кб2Ювен._право(1).doc
#
27.11.2019155.06 Кб8юююююююююху.docx