Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский химико-технологический университет им. Д.И. Менделеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Элементы-алгебры-Шайкин-А.Н

..pdf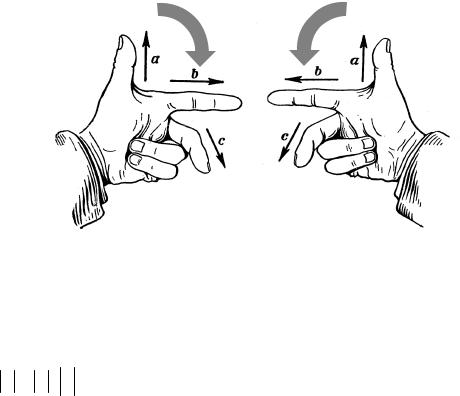

Скачиваний:

554

Добавлен:

12.03.2016

Размер:

1.95 Mб

Скачать

☆

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

1.3. Векторное произведение векторов

Определение. Упорядоченная тройка некомпланарных векторов называется правой тройкой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки (рис. 1). В противном случае она называется левой тройкой.

Левая тройка	Правая тройка
	Рис. 1

При перестановке в упорядоченной тройке двух любых векторов тройка меняет ориентацию на противоположную.

Определение. Векторным произведением а b неколлинеарных

векторов а и b называется вектор с , такой, что: 1. с а b sin a;b ;

2.c a и c b ;

3.вектор с направлен так, что векторы а, b и с в указанном порядке образуют правую тройку.

В случае, если векторы а и b коллинеарны, их векторное произведение равно 0.

Свойства векторного произведения:

1.а,b : а b b а (антикоммутативность).

2.а: а а 0.

3.а,b,с; , R: ( а b) с (а с) (b с)

(линейность).

Подобно тому, как это было сделано для скалярного произведения, можно получить выражение для векторного произведения векторов через их координаты в заданном базисе. Чтобы записать их в компактной и удобной для запоминания форме, нам потребуется понятие определителя.

Определение. Рассмотрим четыре числа: а, b, с и d. Из них можно

составить таблицу	2 2:	a	b	,	которая называется квадратной матрицей
составить таблицу	2 2:		d	,	которая называется квадратной матрицей
второго порядка.		c	d
второго порядка.
Определение.	Числа а,		b	,	с и d называются элементами матрицы.

Элементы a и b образуют первую строку матрицы, элементы c и d – вторую строку; элементы а и с образуют первый столбец матрицы, элементы b и d –

второй столбец.

Определение. Число

ad–bc

называется

определителем (или

детерминантом) матрицы

и обозначается так:

Определение. Аналогично, таблица

, составленная из девяти

чисел, называется квадратной матрицей третьего порядка.

Как и в случае матрицы второго порядка, вводятся понятия элементов матрицы, ее строк и столбцов. Строки по-прежнему нумеруются сверху вниз, а столбцы – слева направо.

Определение. Число a

называется

					a1	a2		a3
определителем (или детерминантом) матрицы					b	b		b	и обозначается
					1	c	2	3
					c	c	2	c
	a1	a2	a3		1		2	3
	a1	a2	a3
	b1	b2	b3	. Более полная теория матриц и определителей будет дана позже.
	c1	c2	c3

				Теорема. Пусть е1,е2,е3 – правый ортонормированный базис, и в этом
базисе а ае а е															а е			и b bе					b е b е . Тогда векторное произведение
									1		1		2	2		3	3				1	1	2	2		3		3		е1			е2	е3
а b вычисляется по следующей формуле а b =																														е1			е2	е3
а b вычисляется по следующей формуле а b =																														а			а	а	.
																														1		2		3
				Доказательство. Так как																	е1,е2,е3									b1			b2 b3
				Доказательство. Так как																	е1,е2,е3			– правый ортонормированный базис, то
	е			е			е			1;			е		е , е				е ,		е	е .		Следовательно,										е е			0,	е	е 0,
	е			е			е			1;			е		е , е				е ,		е	е .		Следовательно,										е е			0,	е	е 0,
	1			2				3						1		2		1		3	2		3											1		1		2	2
	е		е			0.					Поскольку,								во-первых,						е				е		е		sin e ;e				,	во-вторых
	е		е			0.					Поскольку,								во-первых,						е				е		е		sin e ;e				,	во-вторых
3		3																							3				1		2			1		2
е1 е3, е2 е3, и в-третьих,																				е1,е2,е3			– правая тройка, то е1 е2													e3 . Аналогично,
е2 е1 e3 ,												е1 е3				e2 ,				е3 е1 e2 ,							е2 е3 e1,							е3 е2 e1.					Тогда
а b					(ае а							е а е ) (bе b е b е )=
					1			1			2		2		3	3			1	1	2	2	3	3

=а1b1 (е1 е1) а1b2

(е1

е2) а1b3

(е1 е3)

+а2b1

(е2

е1) а2b2

(е2

е2) а2b3

(е2 е3)

+а3b1 (е3

е1) а3b2

(е3

е2) а3b3

(е3 е3)=

=аb е аb е а bе +а

b e +а be а b e =

=(а2b3 а3b2)е1 (а1b3 а3b1)е2 +(а1b2 а2b1)е3=

а2

а3

е1

е2

е3

=е

b b

а а а

Теорема. Длина вектора векторного произведения а

численно равна

площади параллелограмма,

построенного на векторах а и b ,

как на смежных

сторонах.

sin a;b

а b

Доказательство.

Sпар

Теорема. Для того чтобы два вектора в пространстве были коллинеарны,

необходимо и достаточно, чтобы их векторное произведение равнялось

Доказательство необходимости.

Если векторы

а и

b коллинеарны, то

а b 0 по определению.

а b 0.

Доказательство

достаточности.

Пусть

Тогда

sin a;b 0. Если а 0 или

b 0,

то векторы а и

коллинеарны,

поскольку нулевой вектор коллинеарен любому. Если

а 0

b 0, то

sin a;b 0. Следовательно,

a;b 0o

или a;b 180o , т. е. векторы а и

b коллинеарны.

1.4. Смешанное произведение векторов

Определение. Смешанным произведением

(a,b,c)

векторов

а,

b и с

называется число, равное скалярному произведению векторного произведения а b и вектора с .

Свойства смешанного произведения:

1.а,b,с : (a,b,c) (c,a,b) (b,c,a) (b,a,c) (c,b,a) (a,c,b)

(полукоммутативность).

2. а,b,с,d; , R: ( а b,c,d) (а,с,d) (b,с,d)

(линейность).

Теорема. Пусть е1,е2,е3 – правый ортонормированный базис, и в этом

базисе

а ае а е

а е

b bе b е

b е

с се с е

с е . Тогда

смешанное

произведение

(a,b,c)

вычисляется по

следующей

формуле

(a,b,c)=

b b b

c1 c2 c3

Доказательство. Так как е1,е2,е3 – правый ортонормированный базис, то

а2

а3

)

(a,b,c)=(а b) с

=(е

а2

а3

с1

с2

с3

(се с е с е )=с

а а а

1 1

2 2

3 3

b b

(Убедитесь

самостоятельно

справедливости

последнего

равенства).

Теорема. Модуль смешанного произведения (a,b,c) численно равен

объему параллелепипеда, построенного на векторах а, b и с , как на смежных

сторонах.

Доказательство. Vпар Sосн H = а b sin a;b h = а b h = = а b c cos (h,c) =а b c cos (h,c) =

=а b c cos (а b,c) =|(a b) c |=|(a,b,c)|.

Теорема. Для того чтобы три вектора а, b и с были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Доказательство

необходимости.

Дано: векторы

а,

b и

компланарны.

Рассмотрим

различные

случаи,

учитывая,

что

(a,b,c)=(a b) c=

sin a;b

cos (а b,c). Если а 0,

b 0

или

с 0, то (a,b,c)=0.

Иначе,

если а

и b

коллинеарны,

то

sin a;b 0.

Следовательно,

(a,b,c)=0. Иначе,

поскольку вектор

а b

ортогонален

плоскости векторов а и b , а вектор с лежит в ней, то а b с . Следовательно,

(а b,c) 90o , а cos (а b,c) 0, и тогда (a,b,c)=0.

Доказательство

достаточности.

Пусть

(a,b,c)=0,

т.е.

sin a;b

cos (а b,c)=0. Если

а 0, b 0 или

с 0, то векторы

а, b и с компланарны, поскольку 0 компланарен с любыми двумя векторами. Иначе, если векторы а и b коллинеарны, то они линейно зависимы, тогда любой вектор с линейно зависим с ними (покажите это строго по определению

линейной зависимости), а тогда векторы а, b		и с	компланарны. Иначе,
cos (а b,c)=0,	т. е. (а b,c) 90o . Следовательно,		а b с . Поскольку
вектор а b ортогонален плоскости векторов а		и b , а вектор с ортогонален
ему, то вектор с	лежит в плоскости векторов а	и b , т. е. векторы а, b и с
компланарны.

1.5. Решение задач на векторы

В задачах, если не оговорено противное, базис считать правым ортонормированным.

Пример 1. В четырехугольнике ABCD точки P и Q – середины сторон BC

и AD, соответственно. Выразить вектор PQ через векторы AB, BC , CD.

					1				1
	Решение. PQ PB BA AQ					BC AB				AD
									2
1		1		1	2		1

	BC AB		(AB BC CD)		AB			CD. Как видим, вектор BC в это
		2		2
2							2

выражение входит с нулевым коэффициентом (отсутствует).

Пример 2. В параллелограмме ABCD точки P и Q – середины сторон BC

и AD, соответственно. Найти координаты																вектора						PQ,		если за				базисные
векторы приняты e AD и e AB.
		1		2			1				1						1			1
							1				1						1			1								1			1
	Решение.	PQ PC CQ						AD					AB					e				e , т. е.				PQ (				;		) в
базисе e1, e2 .							2				2					2		1	2			2						2			2
базисе e1, e2 .
	Пример 3. В пирамиде ABCD точки P и Q – середины ребер AD и BC,
соответственно.		Найти координаты								вектора						PQ			в		базисе e					AB,			e AC,
e AD.																								1				2
e AD.
3										1									1
										1									1
	Решение. PQ PA AC CQ											AD AC									CB
	Решение. PQ PA AC CQ											AD AC									CB
		1			1					2		1							2
1		1			1				1			1										1		1		1
	AD AC		(CA AB)			e				e				e , т. е.					PQ			(	;		;		) в базисе e ,
	AD AC	2	(CA AB)			e				e	2			e , т. е.					PQ			(	;	2	;	2	) в базисе e ,
2		2		2		1	2			2	2				3							2		2		2					1
e2 , e3 .																						7a 5b .
	Пример 4. Дано: a ( 1;2;5), b (1;3;7). Найти																					7a 5b .
	Решение. 7a ( 7;14;35), 5b (5;15;35). Тогда																				7a 5b ( 12; 1;0).
	Пример 5. Проверить, что векторы a ( 1;3) и b (2;2) на плоскости не
коллинеарны, и разложить вектор c (7; 5)															по базису a,b .

Решение.

Так

как

, то

векторы

не

коллинеарны.

c xa yb .

Следовательно, они образуют базис

на плоскости.

Тогда

Расписывая по каждой координате, получаем уравнения

7 x ( 1) y 2 и

2 x 3 y 2, откуда x 3,y 2. Таким образом, c 3a 2b .

Пример 6. Найти длину вектора

a ( 3;4)

на

плоскости

и вектора

b (1; 2;2) в пространстве.

Решение. |a|

5, |b |

( 3)2

12 ( 2)2 22 3.

Пример 7. Найти направляющие косинусы вектора

AB,

если A(1; 1;3),

B(2;1;1).

Решение.

AB=(1;2; 2).

Тогда

| AB|

Следовательно,

1 4 4

cos 1, cos 2, cos 2. 3 3 3

Пример 8. Вектор a образует с осями OX и OY углы 60о. Какой угол он образует с осью OZ?

Решение. Так как cos2 60o cos2 60o cos2 1, то	cos	1	.

	2

Следовательно, 45o или 135o .

Пример 9. Вектор a образует с осями координат равные острые углы. Найти эти углы.

Решение. Так как cos2 cos2 cos2 1, то cos 1 . Учитывая,

			1		1				3
что углы острые, cos			1	. Тогда arccos	1	.

			3		3
			3		3
Пример 10. Даны точки A(2;0;1), B(2;1;0), C(1;0;0). Найти угол ABC.
Решение. BA (0; 1;1), BC ( 1; 1;0). Тогда
	BA BC		0 ( 1) ( 1) ( 1) 1 0				1
cos								.	Следовательно,
cos							2	.	Следовательно,
	\| BA\| \| BC\|	02 ( 1)2 12 ( 1)2 ( 1)2 02					2

60o .

Пример 11. Найти проекцию вектора a (1;2;3) на ось l, образующую с координатными осями равные острые углы.

Решение.

качестве

можно

взять

(1;1;1).

Тогда

1 1 2 1 3 1

Пр a

2 3 .

Пример 12. Даны векторы a (1;2; 1) и b (2; 1;3). Найти Прab .

								a b			1 2 2 ( 1) ( 1) 3
								a b			1 2 2 ( 1) ( 1) 3																					3
Решение.			Прab																														.
																															2
																		6
								\|a\|										6
Пример 13. Вычислить определитель																							1			2		.
																							1			2
																							3			5
																							3			5
Решение.				1		2	1 ( 5) ( 2) 3 1.
				1		2
				3		5
				3		5
Пример 14. Вычислить определитель																								1		2		3
																								1		2		3
																								0		1			1	.
																								2		4		5
Решение.
	1	2	3						1	1						0		1							0	1			1 9 2 2 3 ( 2) 1.
	1	2	3
	0 1 1					1						2								3
	0 1 1					1				5		2				2		5		3					2	4
	2	4	5						4	5						2		5							2	4
	2	4	5																							a ( 4;1; 7),											b (2;5;9)
Пример			15.			Являются								ли				векторы								a ( 4;1; 7),											b (2;5;9)		и
c ( 8;13; 3) компланарными?
Решение.					4	1			7						5			9							2			9						2		5


					2	5		9		4											1									7
					2	5		9		4					13			3			1				8				3	7				8		13
					8	13			3						13			3							8				3					8		13
					8	13			3																											a,		и c
4 ( 132) 1 66 7 66 0.													Следовательно,														векторы									a,	b	и c	–
компланарны.																								и b (2;1;3). Найти a b .
Пример 16. Даны векторы a ( 1;0;1)																								и b (2;1;3). Найти a b .
								i		j			k
								i		j			k
Решение.					a b			1		0			1				0	1							1	1					1		0						Т.е.
Решение.					a b			1		0			1				1	3	i			2				3			j		2		1		k i 5j k .				Т.е.
								2		1			3				1	3				2				3					2		1
								2		1			3

a b ( 1;5; 1).

Пример 17. Найти площадь параллелограмма, построенного на векторах

a ( 1;3) и b (1;2).

Решение. Вводя третью координату, получаем a ( 1;3;0)							и b (1;2;0).
		1	3

						0 0 ( 5)2 5.
Тогда S \|a b \| \|0i 0j		1	2	k \|		0 0 ( 5)2 5.
		1	2
Пример 18.	Найти	площадь			треугольника с вершинами		A( 1;0; 1),

B(0;2; 3), C(4;4;1).

Решение. AB (1;2; 2), AC (5;4;2). Тогда

		1									1				2				2									1 2													1	2													1																		18

																																																											2						2						2
S				\|a b \|									\|											i													j										k			\|							12				( 12)						( 6)							9.
S		2		\|a b \|							2		\|		4		2							i				5	2								j				5	4					k			\|					2		12				( 12)						( 6)						2	9.
		2									2				4		2											5	2												5	4													2																		2
		Пример 19.													Даны									векторы a и b . Выразить векторы x (a b) (a b) и
	(a b)											a
y								(b						) через вектор																				z a b .
y		2						(b				2		) через вектор																				z a b .
		2										2
		Решение. По свойствам векторного произведения
					x (a b) (a b) a a b a a b b b 2(a b) 2z ,
			(a b)													a				1														1													1													1								3						3
y										(b							)								(a b)												(b b)													(a a)												(b	a)						(a b)						z .
y				2						(b					2		)			2					(a b)									2			(b b)										4			(a a)										4		(b	a)					4	(a b)					4	z .
				2											2					2														2													4													4								4						4
		Пример 20. Найти																								объем параллелепипеда																																			ABCDABC D											и	высоту,
																																																						ABCD,											1			1	1	1
опущенную из вершины																										A1				на основание																								ABCD,							если				A(1;2;3),								B(9;6;4),
D(3;0;4), A1(5;2;6).
		Решение.									AB (8;4;1),																		AD (2; 2;1),																				AA1 (4;0;3). Тогда
																																	8					4				1
																																	8					4				1
									V \|(AB,AD,AA1)\| \|																								2				2					1				\| 48. Площадь основания
																																	4					0				3
																		i							j			k
																		i							j			k
																																				62 ( 6)2 ( 24)2
	S \| AB AD\| \|																	8						4				1			\|					62 ( 6)2 ( 24)2																							18					2 . Тогда высота
																		2			2						1
																																								V					4							.

																																	h																2
																																	h
																																								S		3											ABCD и высоту, опущенную из
		Пример 21. Найти объем тетраэдра																																																			ABCD и высоту, опущенную из
вершины D, если A(0;0;2), B(3;0;5), C(1;1;0), D(4;1;2).
		Решение.									AB (3;0;3),																		AC (1;1; 2),																				AD (4;1;0). Тогда
							1																				1					3		0				3									1											1
																																3		0				3

		V							\|(AB,AC,AD)\|																				\|			1		1						2				\|						\| 3\|									. Площадь основания
		V					6		\|(AB,AC,AD)\|																		6		\|			1		1						2				\|			6			\| 3\|								2	. Площадь основания
							6																				6					4		1				0									6											2
																																4		1				0
																							i					j				k

				1													1																					1																								3 11

																																																	2							2			2
	S					\|		AB AD\|												\|		3					0		3						\|								( 3)								9						3									. Тогда высота
	S			2		\|		AB AD\|												\|		3					0		3						\|			2					( 3)								9						3						2			. Тогда высота
				2													2					1					1					2						2																									2
																						1					1					2

																																	h						3V									1						.

																																								S							11
																																								S							11

1.6. Задачи для самостоятельного решения

Задача 1. Вычислить определители:

а)

;

б)

;

в)

cosx

sinx

;

г)

log

e a

sinx

cosx

logb a

Задача 2. Решить уравнения:

x 2

а)

б)

x 2

в)

sinx 1

sinx 2

г)

log2 x 3

sinx

log2 x 3

log2 x

Задача 3. Вычислить определители:

cosx

sinx

а)

5 3 2

;

б)

2 4

;

в)

b c d

;

г)

sinx

cosx

Задача 4. Решить уравнения:

а)

x 0

б)

1 x

a x

в)

a x

г)

b x

c x

Задача 5. Написать разложение вектора x по векторам p,q,r :

а)

x (0; 8;9), p (0; 2;1),q (3;1; 1),r (4;0;1);

б)

x (8; 7; 13), p (0;1;5),q (3; 1;2),r ( 1;0;1);

в)

x (2;7;5), p (1;0;1),q (1; 2;0),r (0;3;1);

г)

x ( 15; 20; 1), p (0;2;1),q (0;1; 1),r (5; 3;2).

Задача 6. Коллинеарны ли векторы с1и с2 ,

построенные по векторам a и

b ?

3b,c

9b 12a;

а)

a ( 1;2;8),b (3;7; 1),c

б)

a (2;0; 5),b (1; 3;4),c

5b,c

2b ;

в)

a (4;2; 7),b (5;0; 3),c

a 3b,c

6b 2a ;

b 3a.

г)

a ( 1;3;4),b (2; 1;0),c

2b,c

Задача 7. Найти угол между векторами ABи AC :

а)

A(1;4; 1),B( 2;4; 5),C(8;4;0);

б)

A(0;1;0),B(0;2;1),C(1;2;0);

в) A( 4;0;4),B( 1;6;7),C(1;10;9);

г) A( 2;4; 6),B(0;2; 4),C( 6;8; 10).

Задача 8. Вычислить площадь параллелограмма, построенного на векторах a и b :

а) a

6p q,b 5q p,

1/ 2,

4, p;q 5 / 6;

б) a

2p 3q,b p 2q,

1, p;q /3;

в) a

2p 3q,b 5p q,

3, p;q / 2;

г) a

3p 2q,b 2p q,

4, p;q 3 / 4.

Задача 9. Компланарны ли векторы a, b и c ?

а) a (4;1;1),b ( 9; 4; 9),c (6;2;6);

б) a ( 3;3;3),b ( 4;7;6),c (3;0; 1);

в) a ( 7;10; 5),b (0; 2; 1),c ( 2;4; 1);

г) a (7;4;6),b (2;1;1),c (19;11;17).

	Задача 10. Вычислить объем тетраэдра с вершинами в точках A1,A2,A3, A4
и его высоту, опущенную из вершины A4 на грань A1A2 A3:
а)	А1( 2; 1; 1), A2(0;3;2),A3(3;1; 4),A4( 4;7;3);
б)	А1( 3; 5;6), A2(2;1; 4),A3(0; 3; 1),A4( 5;2; 8);
в)	А1(2; 4; 3), A2(5; 6;0),A3( 1;3; 3),A4( 10; 8;7);
г)	А1(1; 1;2), A2(2;1;2),A3(1;1;4),A4(6; 3;8).

Задача 11. Найти расстояние от точки M0 до плоскости, проходящей

через точки M1,M2,M3 :

а) M1(1;1;2), M2( 1;1;3),M3(2;3;8),M0(2; 2;4);

б) M1(2;3;1), M2(4;1; 2),M3( 5; 4;8),M0(6;3;7);

в) M1(1;1; 1), M2(2;3;1),M3( 3; 7;6),M0(3;2;1);

г) M1(1;5; 7), M2( 3;6;3),M3(1; 1;2),M0( 2;7;3).

Задача 12. Найти единичный вектор, перпендикулярный плоскости ABC:

а) A( 1;2; 2),B(13;14;1),C(14;15;2);

б) A(7; 5;0),B(8;3; 1),C(8;5;1);

в) A( 3;6;4),B(8; 3;5),C(0; 3;7);

г) A(2;5; 3),B(7;8; 1),C(9;7;4).

Задача 13. Найти угол между плоскостями:

а)	x y z	2 1 0, 3x y z		2 5 0;
б) 3x y 5 0, 2x y 3 0;
в)	x y z		3 0, x y z		1 0;
		2		2

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.09.20194.78 Mб3Экзаменационный билет N 19.doc
#
13.02.2015125.44 Кб24Экология курсовая.doc
#
13.02.201529 Кб16экология.docx
#
13.02.2015133.04 Кб8ЭКОНОМ ЗАЧЕТ.docx
#
15.04.2019591.87 Кб0экономика_7 задание.doc
#
12.03.20161.95 Mб554Элементы-алгебры-Шайкин-А.Н..pdf
#
23.11.2019144.38 Кб51Эпоксидные смолы.doc
#
13.02.201513.76 Mб51Эффект Комптона.doc
#
26.11.201965.02 Кб1Ювен._право(1).doc
#
27.11.2019155.06 Кб3юююююююююху.docx
#
18.08.2019105.47 Кб6языкознание.doc